欢迎关注微信公众号「Swift 花园」
很多人喜欢吃巧克力,但多数人吃巧克力是比较谨慎的。因为吃了太多巧克力,很有可能会增加体重。在这一期的教程中,我将讨论如何使用表格和图表展示 两个变量之间的关系 。这有助于发现两个变量之间是否存在 相关性 (correlation) 。
列联表 (Contingency Tables)
我们来进一步研究吃巧克力和体重之间的关系。
假设我在我们学校选择了 200 名女学生。她们身高都是一米七。这样,身高就是一个常数,不会影响体重或吃巧克力。让学生报告体重及每周巧克力消费情况。体重可以选择这样几个类别:小于 50 公斤; 50 至 69 公斤; 70 至 89 公斤和 90 公斤或以上。巧克力消费量可以选择这样几个类别:每周少于 50 克;每周 50 至 150 克;每周超过 150 克。
结果如下,这里看到的是 列联表 。 列联表 能够显示 两个定序或定类变量之间的关系 。 它类似于频率表,但主要区别在于 频率表始终只考虑一个变量,而列联表考虑两个变量 。
在我们的研究中,有两个变量:体重和巧克力消费量。
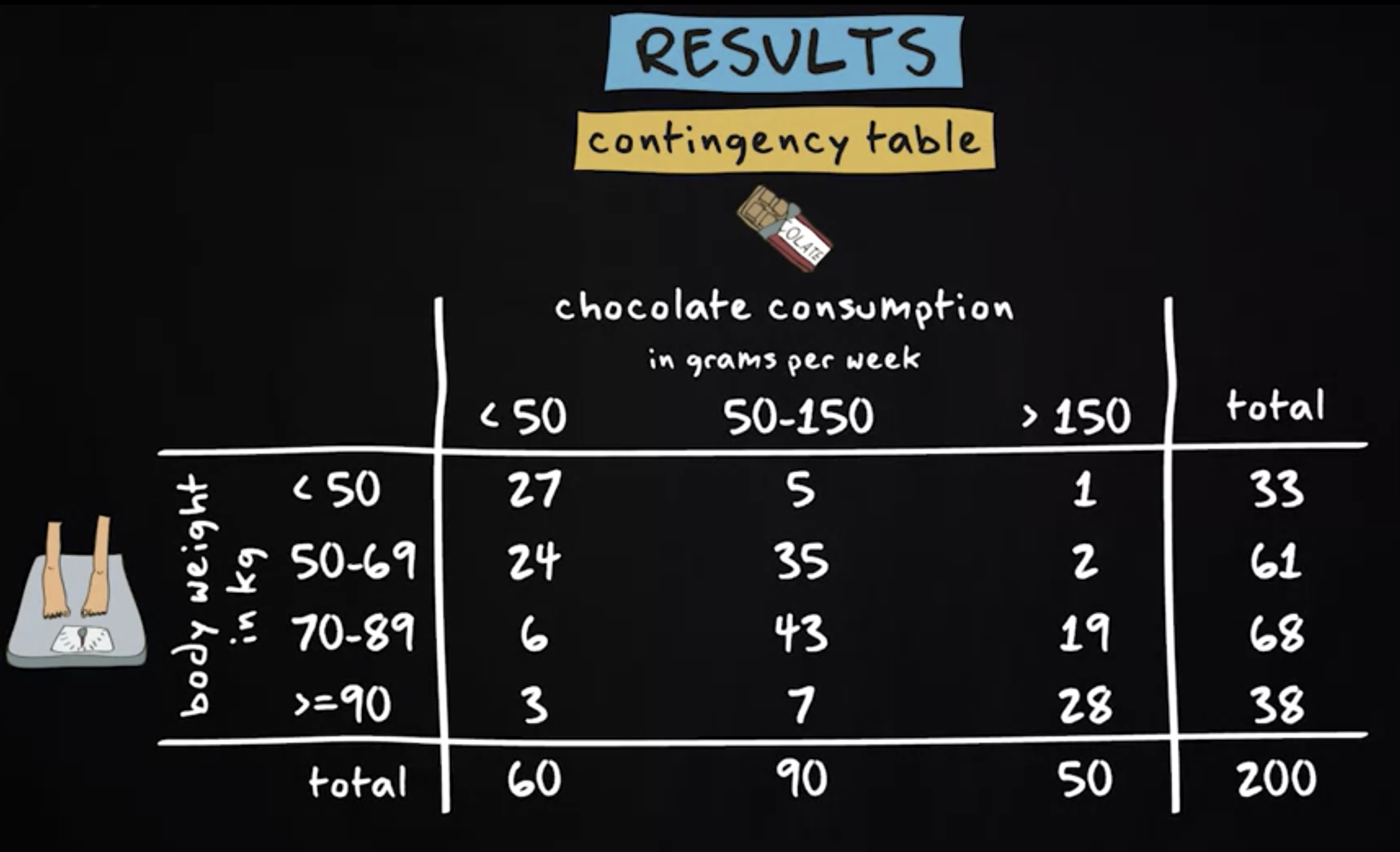
该表显示我们有 33 个体重小于 50 公斤的样本 其中 27 人每周吃巧克力少于 50 克。还可以看到,每周有 90 人吃 50 至 150 克巧克力,其中 7 个体重 90 公斤及以上。
这种情况下,该表并不能提供两个变量之间的相关性信息,因为列和行包含不同数量的个案 —— 计算百分比可以提供更多洞察力。这种情况下,我们计算列的百分比,这意味着对于每个单元格,我们计算该单元格中的案例百分比,与相应列中的案例总数进行比较。
结果如示:

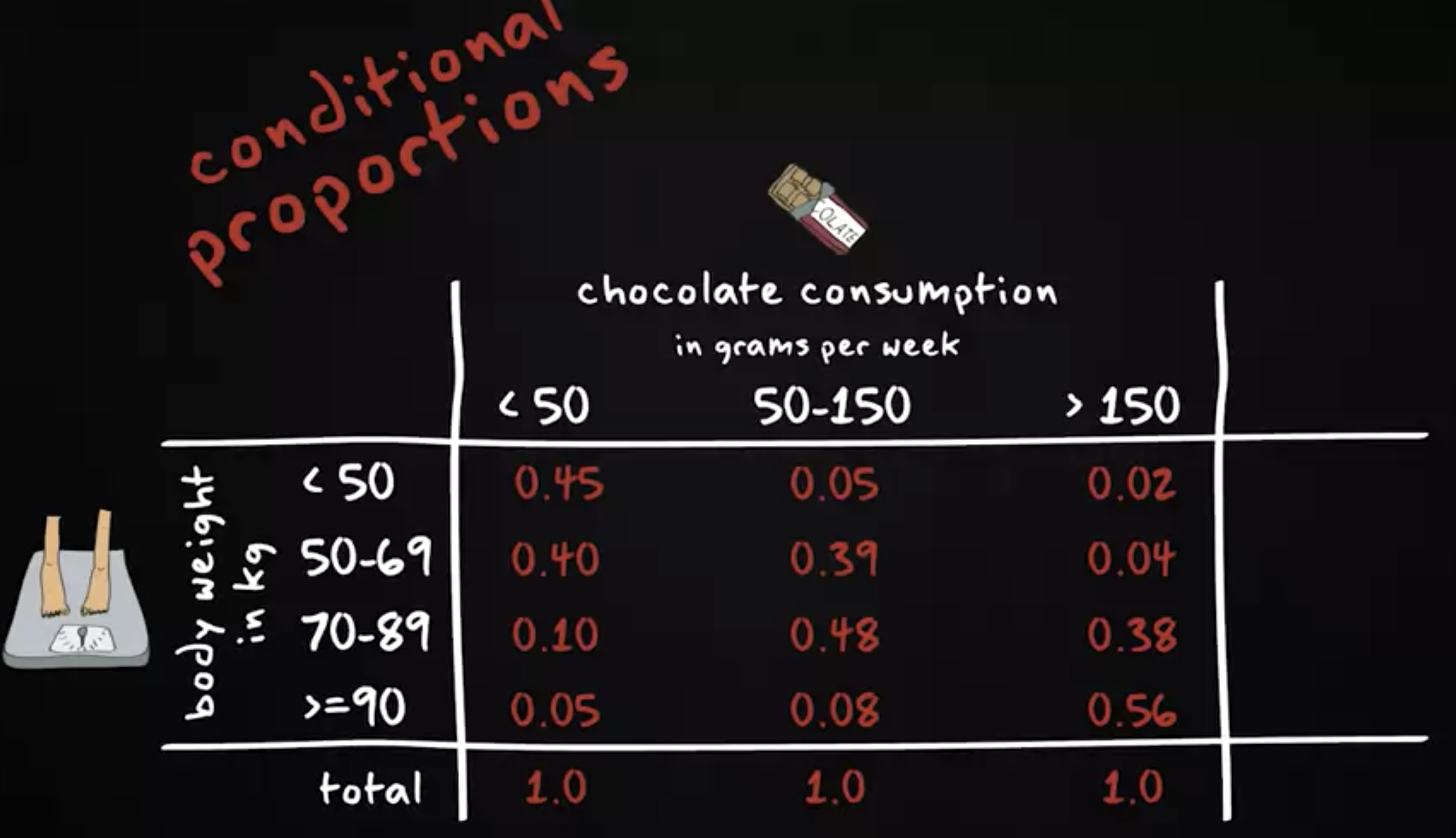
我们也可以将这些百分比表示为比例: 45% 则变为 0.45, 38% 变为 0.38 。我们将这些比例称为 条件比例 (conditional proportions) —— 因为形成需要以另一个变量为前提条件。在这种情况下,该变量是巧克力消费量。
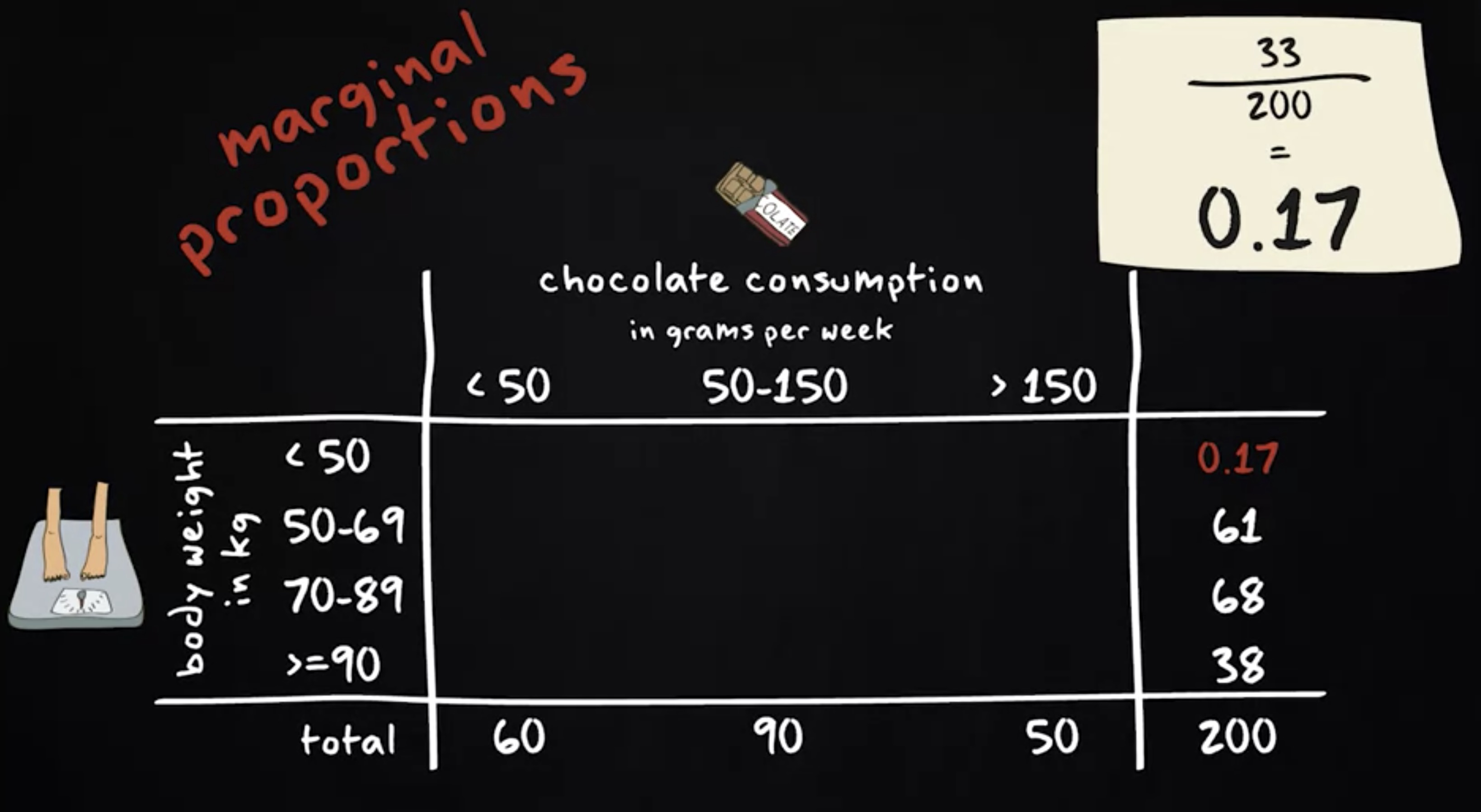
我们也可以忽略巧克力消费的信息,并使用表格边缘的计数。这些都是 边际比例 (marginal proportions) 。例如, 33 除以 200 等于 0.17 。这个比例显示,研究中比例是 0.17 或 17% 的受访者中,重量不到 50 公斤。
这是什么意思呢? 在每周吃巧克力超过 150 克的样本中, 56% 的人体重达 90 公斤及以上;吃巧克力少于 50 克的样本中,只有 5% 体重为 90 公斤或以上;另外,那些吃巧克力不到 50 克的人, 45% 的人体重不到 50 公斤,而吃巧克力超过 150 克的人,只有 2% 的体重不到 50 公斤。

这些百分比表明:吃更多巧克力的人也更容易超重,而少吃巧克力的人也更可能体重较小。换句话说,百分比表明巧克力消费量与体重之间存在相关性。
散点图 (Scatterplot)
- 列联表对定类和定序变量很有用,但不适用于定量变量。对于定量变量,散点图更合适。 假设没有提供类别,而是让 200 名女性给出确切的体重,例如 65 或 72 公斤。假设也要求他们告知每周吃巧克力的确切重量,例如每周可以是 64 克或 99 克。现在,有比之前更精确的信息展示定量变量,巧克力消费和体重之间关系的最佳方法是使用 散点图 。
制作散点图,我们绘制两条线,称之为 轴 。我们将水平轴称为 X 轴 。这里展示的是 自变量 (independent variable) ,垂直轴称为 Y 轴 ,我们用它来表示 因变量 (dependent variable) 。如果因变量和自变量之间没有区别,则 Y 轴和 X 轴上的位置是一个选择问题。在我们的例子中,自变量是巧克力消耗量,因变量是体重。
假如我们的研究表明,最少的巧克力消耗等于每周零克,最高的量是每周 700 克。我们在 x 轴上标注这些值;同样,体重的最小值为 40 公斤,最大值为 110 公斤。
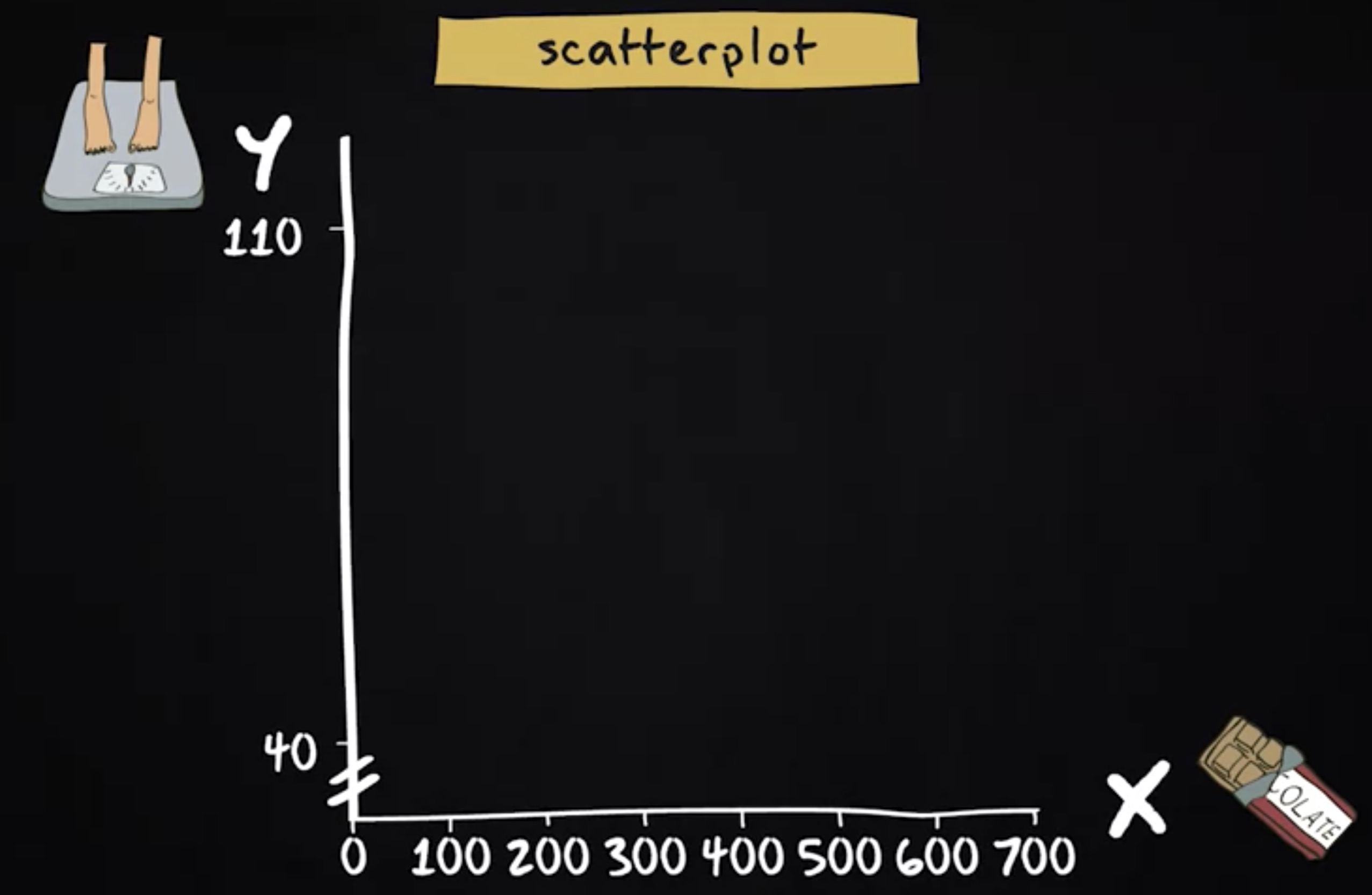
接着我们在此图中显示每个人,为样本中的所有人做标注,这就绘制出了一幅散点图。散点图一目了然地显示巧克力消费量与体重之间存在相关性:吃的巧克力越多,体重就越高。
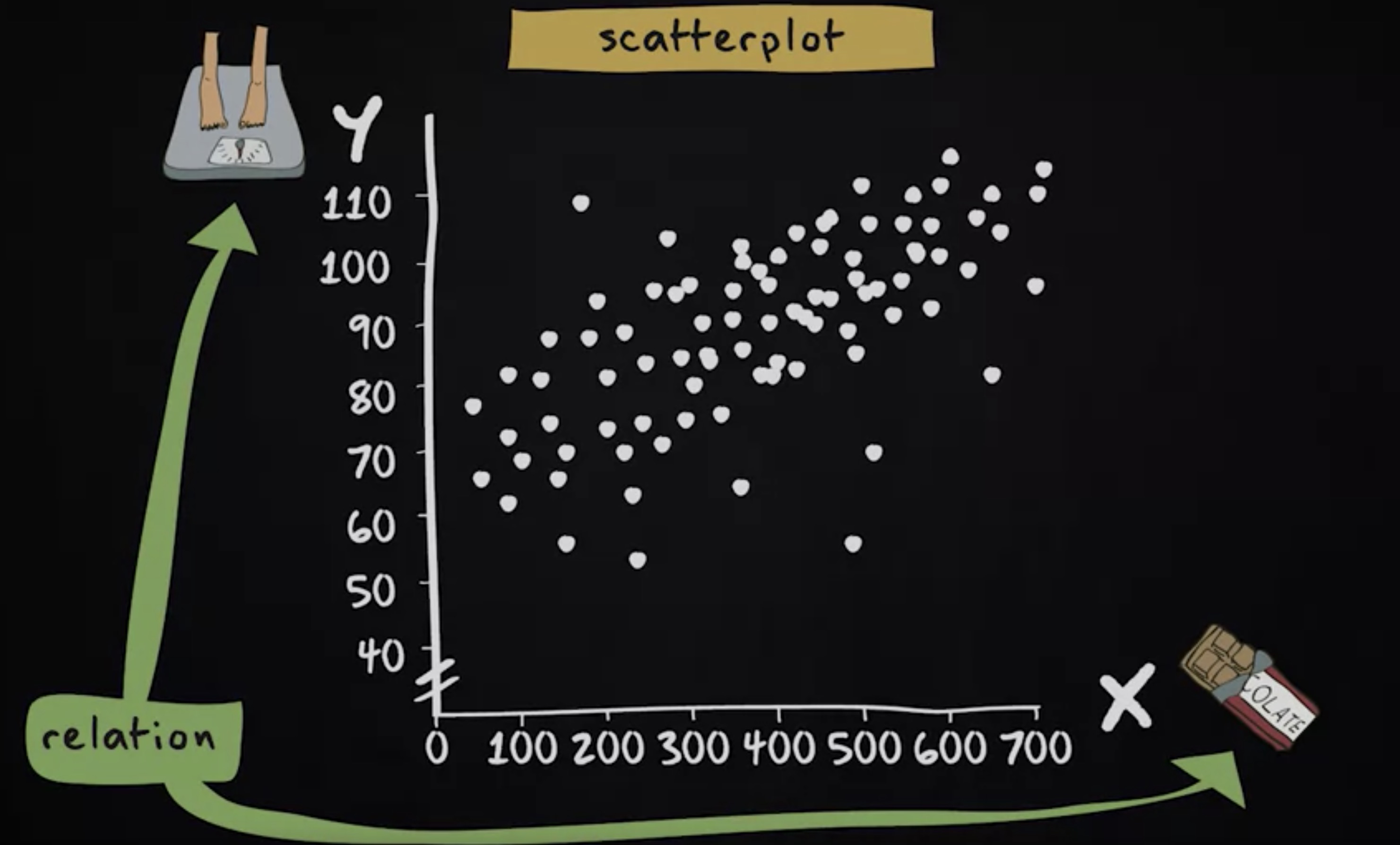
小结
大家学到了什么呢?不止于巧克力消耗量和体重的相关关系,我想大多数人已经意识到了:我们可以通过表格和图表显示 两个变量之间的关系 ,当研究中的变量是定类或定序变量时,我们使用列联表;当它们是定量测量时,我们使用散点图 。
皮尔逊积矩相关系数 (Pearson’s r)
散点图一目了然地表明两个变量之间存在很强的相关性,但 这种相关性有多强 ?我们现在将要讨论最常用的相关性度量方法之一 —— 皮尔逊积矩相关系数 。皮尔逊相关系数最重要的优点之一是:它用一个数字表示两个变量之间线性相关的 方向 和 强度 。
巧克力消费和体重之间的关系可以用这条直线来描述。因为所有案例都紧密围绕这条线,所以可以得出结论,这是一个相当强的相关性关系。
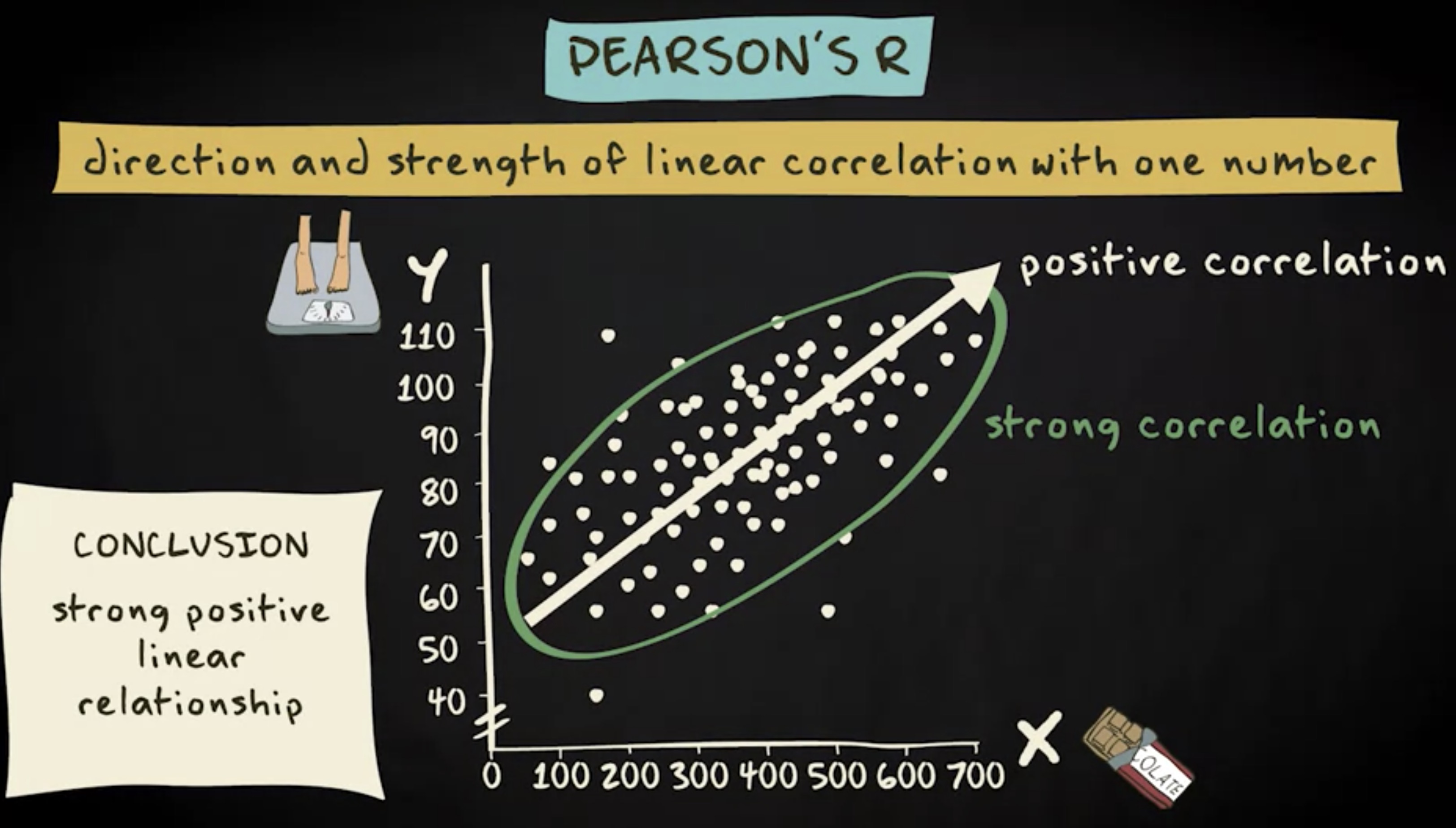
另一个需要注意的点是,直线向上延伸,表明更多的巧克力消耗与更高的体重相关。因此,也可以说存在 正相关 关系。结论:这里存在一个强正向线性关系。
然而,变量也可以以不同的方式相关联。
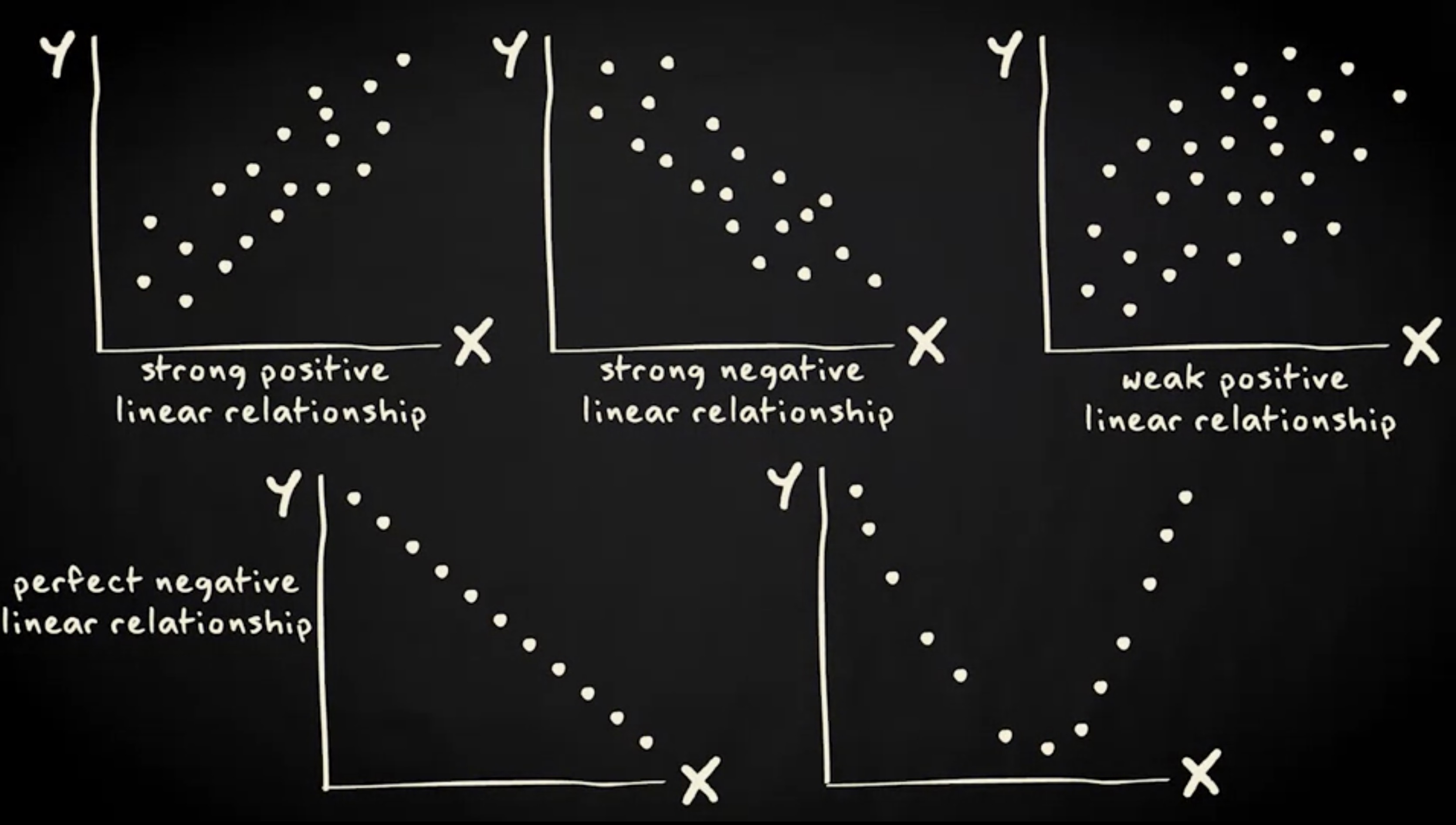
在上图的第一幅图中,可以看到变量 x 和 y 之间存在相当强的正向线性关系,如同巧克力消费和体重的示例一样;而在第二幅图中,存在一个相当强的负向线性相关性 —— 直线向下表示当变量 x 上升时,变量 y 下降。第三幅图也可以看到正向线性关系,但是它比之前的强度要小得多 —— 因为每个案例都远离直线。第四幅图则是一个完全负向线性相关。之所以说完全的,是因为所有案例都完全落在线上。
但两个变量之间的相关性不必是线性的。在第五幅图中,可以看到变量 x 和 y 之间的关系。最能代表两个变量之间关系的线并不是直线。相反,是一个 U 形线,我们称之为曲线关系。
散点图有助于我们总体评估相关性是强还是弱,但它并没有告诉我们这种关系强度到底是多少。皮尔逊相关系数恰巧可以展示确切数字 —— 更具体地说,皮尔逊相关系可以告诉我们 两个定量变量之间线性关系的方向和精确强度 。正皮尔逊相关系数表示相关性为正,而负系数表示相关性为负。
系数的大小表示 观测结果围绕数据假想最佳拟合直线的紧密程度 。皮尔逊相关系数是始终介于 -1 和 1 之间的数字:负 1 表示完全负相关;正 1 表示完全正相关; 0 表示完全没有相关性。
那如何计算皮尔逊相关系数呢?试想巧克力消费和体重的研究不是 200 个样本,而是四个样本。
下面是数据矩阵和散点图:

可以看到两个变量的每个值的组合在图形中变为一个圆点。要计算皮尔逊相关系数,我们需要这个公式:
这是什么意思呢?首先将所有原始分数改为 z 分数,换句话说,标准化所有数值 —— 原因是我们希望皮尔逊相关系数是介于 -1 和 1 之间的数字 。如果不进行标准化,相关性将会以原始数据呈现。
首先,我们计算两个变量的均值:变量 x 的值为 162.5 ,即巧克力消耗量;变量 y 的值为 71.25 ,即体重。然后计算两个变量的标准差, x 的结果为 110.9 , y 的结果为 18.4。再然后计算每个案例的 z 分数,从每个值中减去均值,然后除以标准差。
为自变量的每个值,即巧克力消耗量,因变量的每个值,即体重,进行如此计算。下一步,计算 y 值 z 分数和 x 值 z 分数的乘积。

计算公式的最后一部分,将所有这些 z 分数的乘积相加,将得数除以 n 减 1。所以在我们的例子中,皮尔逊相关系数是 2.78 除以 (4 - 1) ,等于 0.93 。这是什么意思呢 —— 这意味着巧克力消费与体重之间存在强烈的正向线性关系。
一个重要注意事项:即使关系是非线性的,也可以随时计算皮尔逊相关系数。因此,在计算皮尔逊相关系数之前,要先检查散点图看变量是否存在线性相关 ,这一点非常重要。如果不存在,就不要计算皮尔逊相关系数,因为它就不能提供太多变量关系信息。
例如,下面这个散点图显示 x 和 y 之间存在强烈的 曲线关系 。如果计算皮尔逊相关系数,会得到一个非常低的值,负 0.15 。这并不能说相关性较弱,只能说线性相关性较弱。

小结
计算四个样本的皮尔逊相关系数是相当容易的。但是,可以想象,当样本是 200 个时,这几乎是不可能完成的任务。幸运的是,每个统计程序都可以快速计算皮尔逊相关系数。然而,重要的是要了解皮尔逊相关系数究竟意味着什么。了解公式的含义也很重要,它可以帮你更好地理解变量的相关性,也可能会帮你决定 “每周吃多少巧克力。” :)

