欢迎关注微信公众号「Swift 花园」
当我们向他人呈现数据时,通常需要将数据 “总结” 成各种图表的形式,例如频率表、饼图、条形图、散点图和直方图等。
统计案例、变量和测量级别
如果你对足球非常感兴趣,你想知道所有细节:比如某个球员有多少进球,某个球队赢了多少场比赛或者在某场足球比赛中有多少次点球。统计学知识,将帮助你成为足球或任何其他运动的真正专家。
进球得分,赢得比赛,判罚点球,这些都可以被看作 变量 和 统计案例 。
变量 是事件或者人物的特征, 统计案例 就是那个事或那个人。
来讲得更具体一点。想象一下,你最喜欢的球队,你对足员的某些特征感兴趣:你想知道他 / 她的体重,头发颜色,年龄以及在最近的比赛中得分的总数。所有这些球员的特征都是变量,球员本身就是统计案例。
另一个例子,可能你对个别球员的特征不是那么感兴趣,而对他们所效力的球队特征感兴趣。例如,你可能想了解每个西班牙球队,以及它们所在的城市,他们队服的主色调是什么,以及球队去年有多少进球。这些特征也都是变量。但是,这里的统计案例不是个别球员,而是这些人所效力的球队。
在一项研究中,案例可以是许多不同的事物。 可以是个别球员和球队,也可以是公司,学校甚至是国家。
案例的每个特征都可以成为变量 —— 只要它符合一个基本的标准:即是变化的
这是什么意思呢? 让我们回到示例。以球队为案例,并以团队所在的城市为变量。你关注每个西班牙球队,所以会有很多不同的城市:一支球队来自巴塞罗那,其他球队来自马德里,瓦伦西亚或塞维利亚。换句话说,城市是有变化的。
现在让我们关注另一个特征,不是城市,而是球队所在的国家。对于每一个球队而言,它们的国家都是西班牙 这些球队都是西班牙球队。这表示它们之间没有差异:没有一支球队会来自西班牙以外的其他国家。出于这个原因,这个特征不是变量,而是常量。
可以想象,我们可以有许多不同类型的变量代表非常不同的特征。因为这个原因,还有一些其他原因(我之后会讨论到)区分不同的 测量级别 至关重要,
最简单的测量是 定类测量 。定类变量由彼此不同的各种类别组成 变量之间没有顺序关系。 这意味着无法区别一个类别比另一个更好或更差,更多或更少。一个例子是球员的国籍,各种类别,例如西班牙,法国或墨西哥。彼此不同,但没有排名顺序;另一个例子是球员性别或球队所在城市。
第二级测量是 定序测量:变量的类别之间不仅存在差异,还存在顺序 。例如球赛的排名:可知谁是冠军,谁是第二,第三,等等。但是,通过查看排名,你不可能知道类别之间的差异大小 例如,你不知道第一名比第二名好多少。
定类和定序测量都可以称为分类变量。
下一级测量是 定距测量。在定距变量中:我们有不同的类别和顺序,类别之间也有相似的区间。 一个例子是球员的年龄。我们可以说,18 岁的球员与 16 岁的球员,年龄不同。另外,我们可以说这个球员年纪大些。就年龄而言,我们也可以说:18 岁球员和 16 岁球员之间的年龄差异,类似于 14 岁球员和 12 岁球员之间的年龄差异。
最高级的测量是 定比测量 。它类似于定序测量,但另外还有一个有意义的零点。例如球员的身高,以厘米为单位。它们在类别上存在差异,有一定的顺序,有相似的间隔,也有一个有意义的零点。身高为 0 厘米意味着没有高度。请注意,我们不能说年龄有一个有意义的零点:因为零岁并不意味着没有年龄,因此年龄是定距变量。
定距和定比变量就是我们所说的 定量变量 ,因为类别由数值表示。
定量变量也可以分为 离散变量 和 连续变量 。如果某类别形成一组单独的数字,则变量是离散的。例如,球员的进球数:球员可以进一球或两球,但不能是 1.21 球。如果变量值形成区间,则变量是连续的。一个例子是玩家的高度:有人可能是 170 厘米或 171 厘米高,也可能是,比如说,170.2461 厘米高。我们没有一组单独的数字,而是一个无限的数值区域。
区分测量级别的意义
为什么区分这些不同的测量等级如此重要。因为 我们用来分析数据的方法,取决于变量的测量水平。
然而,在实践中, 区别有时会变得模糊。 例如,对于许多统计分析,定距和定比测量之间的差异并不重要。此外,许多统计学家认为,如果定类测量有十分类甚至更多分类,就可以定量分析这些变量。
一个例子是调查问卷,问题是从 0 到 10 之间你如何评价某个球员。在形式上,这是一个定类变量,但在实践中,你可以讨巧将其视为定量变量。
小结
从案例,变量和这些变量的衡量水平来考虑球员,球队和比赛,可以让你对足球有更结构化的理解。
数据矩阵
我们已经知道实施一项研究,可以根据案例和变量来考虑。接下来,我将讨论如何排布和展示你的案例和变量。
想象一下,你对西班牙顶级球赛 “西班牙甲级联赛” 感兴趣。你感兴趣的案例是联赛的个体球员,你关注的变量是年龄,体重,进球数量,会籍和头发颜色。
排布所有这些信息的最佳方式是通过 数据矩阵 。数据矩阵是所有统计研究的核心要素:它是所有案例和变量的概述。 案例显示在行中 ,它的范围从 1 号球员一直到 400 号球员。
| 球员 | 年龄 | 体重 | 进球数 | 会籍 | 头发颜色 | |
|---|---|---|---|---|---|---|
| 球员 1 | 18 | 72.6 | 0 | Real Zaragoza | 金发 | |
| 球员 2 | 21 | 71.4 | 0 | Real Betis | 黑发 | |
| 球员 3 | 26 | 74.8 | 8 | Sevilla | 黑发 | |
| 球员 4 | 22 | 76.8 | 12 | Barcelona | 黑发 | |
| 球员 5 | 22 | 74.1 | 17 | Valencia | 其他 | |
| 球员 6 | 27 | 78.9 | 3 | Real Sociedad | 其他 | |
| 球员 7 | 30 | 80.3 | 2 | Real Madrid | 金发 | |
| 球员 8 | 24 | 73.3 | 1 | Athletic Bilbao | 褐发 | |
| 球员 9 | 23 | 76.9 | 5 | Valencia | 褐发 | |
| … | … | … | … | … | … | |
| 球员 24 | 26 | . | 0 | Malaga | 黑发 | |
| … | … | … | … | … | … | |
| 球员 400 | 26 | 77.2 | 0 | Atheletic Madrid | 其他 |
这里没有显示名字,这意味着这里的名称是匿名的。 变量显示在列中 。我们有五个变量:年龄,体重 进球数,会籍和头发颜色。表格单元格中显示的值通常称为 观测值 。这里 80.3 表示 7 号球员的体重是 80.3 公斤,这里的八分表示三号球员已经进了八球。
我们看到的不是一个完整的数据矩阵,只是其中一部分。完整的矩阵无法单屏呈现,因为它有 400 行,因为我们有 400 名球员。省略号已经明确表示只取了矩阵的一部分。
来看看我们的数据矩阵是否包含异常值。嘿,其中的 24 号球员,我们看不到体重数值。目前,我们已经囊括了这些不完整的案例。但是,如果后续分析需要完整的数据矩阵,我们可能必须删除它们。
所有统计分析都需要数据矩阵。但是,你通常不会向其他人提供完整的数据矩阵。原因是数据矩阵通常很大。在我们的例子中,有 400 行,并且也没有清楚地概述数据矩阵中包含的统计信息。
当我们将数据矩阵中的信息呈现给其他人时,经常以表格和图形的形式进行数据摘要。想象一下,你想要概述西班牙足球比赛中关于球员头发颜色的信息。较好的方法是制作频率表。频率表显示案例中 变量数值的分布 。 频率表就是变量的所有可能值的列表,连同每个值的观测次数。
这是一个基于发色变量的示例,我们可以区分四个类别 金发,棕色,黑色和其他。
| 发色 | 频率 | 百分比 | 累积百分比 | |
|---|---|---|---|---|
| 金色 | 76 | 19 | 19 | 19 |
| 褐色 | 134 | 33.5 | 52.5 | |
| 黑色 | 160 | 40 | 92.5 | |
| 其他 | 30 | 7.5 | 100 | |
| 总计 | 400 | 100 |
可以看到 76 名球员是金发, 160 名球员是黑发。注意,这些值相加是 400,所以没遗漏任何头发颜色的数据。
我们还可以通过百分比表示相对频率。在第二列中,可以看到百分比。可以一眼看出 7.5% 球员是其他发色, 19% 的球员是金发。将 76 除以 400 再乘以 100 得到 19 。
有时,研究人员使用累积百分比。这也很容易计算,累积百分比就是每个类别的百分比之和。所以可以看到 19 加 33.5 等于 52.5 金发和棕色头发占比 52.5 。
在这个例子中,我们讨论了一个分类变量,头发颜色。如果处理定量变量怎么办?以体重为例,计算每个特定个体的体重百分比是没有意义的。因为那样我们最终会得到无数的类别 —— 频率表将显示:比如两个人的体重为 65.3 公斤,一个人体重 65.4 公斤,等等。这几乎没比原始数据矩阵提供额外的有用信息。
研究人员通常会建立新的 顺序分类 来解决这类问题。可以做成,例如,第一类包含那些小于 60 公斤的球员;第二类,体重在 60 到 69.9 公斤之间的;下一类,介于 70 和 79.9 之间的;接着介于 80 和 89.9 之间的;最后一类, 90 公斤及以上。像下面这样:
| 体重 | 频率 | 百分比 |
|---|---|---|
| < 60 | 8 | 2 |
| 60-69.9 | 69 | 17.25 |
| 70-29.9 | 273 | 68.25 |
| 80-89.9 | 45 | 11.25 |
| >= 90 | 5 | 1.25 |
| 总计 | 400 | 100 |
虽然这样你可能会丢失信息,但优点是可以获得更好的概述。我们说你已经 重新编码了变量 。体重变量本是定量变量,但现在变成了一个只有五个类别的定序变量。
将定量变量重新编码为定序变量非常容易。但是,反过来是不可能的:你无法将定序变量重新编码为定量变量。所以,你该了解 —— 数据矩阵是所有统计分析的根源 。它是数据的概述。但是,如果你想将发现呈现给他人,可以使用 数据摘要 。一个非常好的总结方法是制作 频率表 。如有必要,你可以将定量变量重新编码为定序变量。
信息图和各种数据分布形状
定类变量
如果想研究西班牙主要足球比赛中的球员来自哪里,下面这个频率表可能就是结果:
| 国籍 | 频率 | 百分比 |
|---|---|---|
| 欧洲 | 280 | 70 |
| 北美 | 16 | 4 |
| 南美 | 56 | 14 |
| 非洲 | 32 | 8 |
| 亚洲 | 16 | 4 |
| 总计 | 400 | 100 |
可以看到 280 名球员来自欧洲, 16 名来自北美, 56 名来自南美, 32 名来自非洲, 16 名来自亚洲。
我还添加了相对百分比,你可能希望通过图表展示百分比,有两种可能的方法。
这里是一个 饼图 。要概述的变量类别是通过饼图 切片 展示在饼图中,切片表示每个类别的百分比,一目了然 —— 几乎四分之三的足球运动员来自欧洲。
另一种概述数据的方法是 柱状图 ,它可以非常清楚地展示数据在各个变量类别上的分布。
柱形的高度代表每个类别观测值的百分比。
饼图和柱状图的优劣
两种图表都各有优,缺点。饼图的一个优点是,可以立即看出大约 75% 的球员来自欧洲,不进行点计算就无法轻松地从柱状图中辨别出这些信息。但是,另一方面,从饼图中不容易检索每个类别的确切球员数量。例如,在柱状图中,可以轻松地看到有 50 多名球员来自南美洲。
如果变量的类别数量增加,柱图优于饼图。 例如,想象一下,不是球员所在大洲,而是他们出生的某个具体国家。图呈现的效果将非常非常混乱。出于美学原因,你可能会在饼图中使用不同颜色,但所有这些信息使饼图不易于理解。在这种情况下,柱状图会更合理。柱状图也会包含大量信息。但它会比花里胡哨的饼图更容易理解。
定量变量
前面讲了定类变量,那么定量变量又要怎么处理呢?
一种可能性是 气泡图 。这个想法很简单,想象一下有 10 个球员身高信息,用厘米表示。
下面是数据矩阵。
| 球员 | 身高 |
|---|---|
| 球员 1 | 176 |
| 球员 2 | 180 |
| 球员 3 | 165 |
| 球员 4 | 177 |
| 球员 5 | 167 |
| 球员 6 | 170 |
| 球员 7 | 175 |
| 球员 8 | 178 |
| 球员 9 | 174 |
| 球员 10 | 172 |
首先,绘制一条水平线,并以规则的间隔标记可能的数值,如下所示。

接下来,对于每次观测在水平线上的数值之上标记一个点,像就这样:

可以想象,当只有若干观测结果时,气泡图很不错。但是,当样本巨大时,会变得混乱。 100 个球员的样本,看起来是这样的:
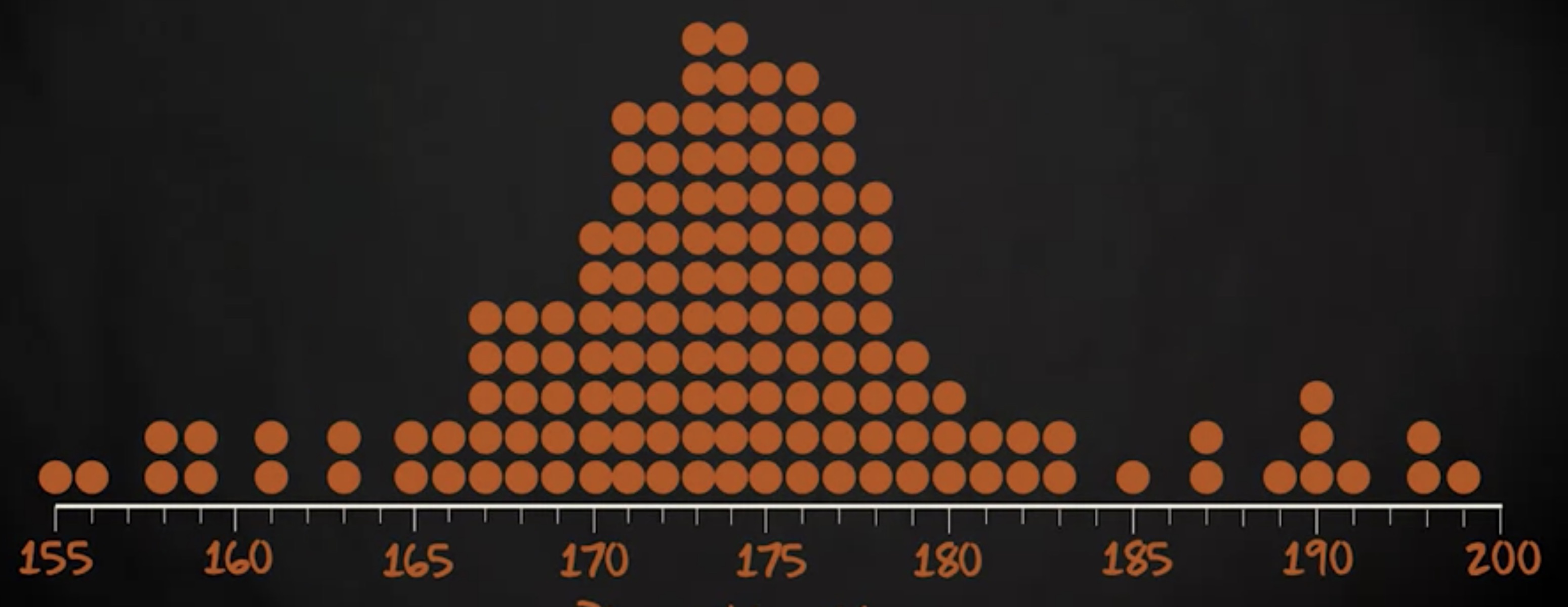
如果有很多观测结果时,研究人员通常会使用另一种类型的图表:直方图
这就是一例:
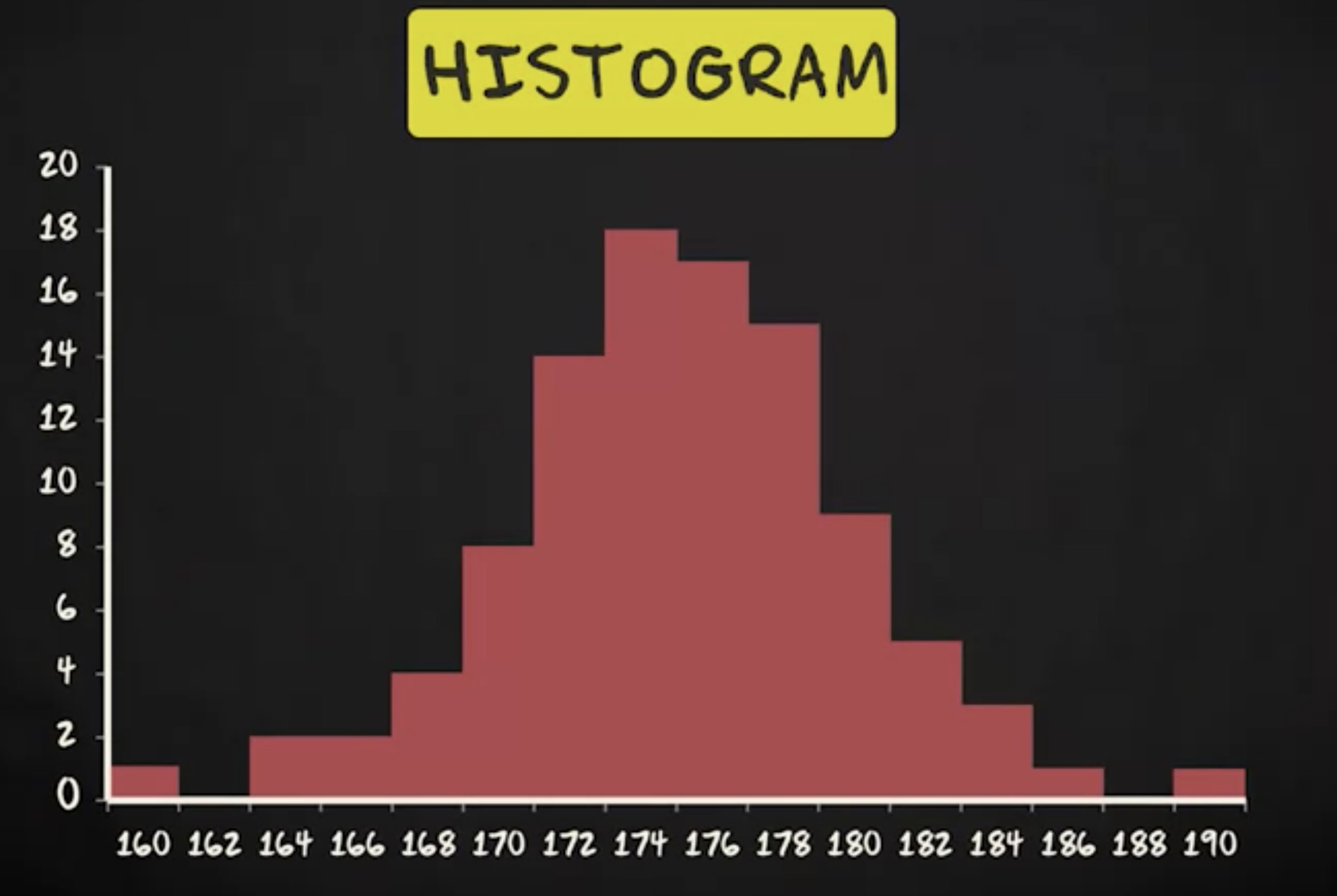
直方图在某种意义上类似于柱状图,它使用柱形来描绘变量可能数值的频率或相对频率。但是,有一个重要的区别: 直方图中的柱点是相互接触的。
该接触表示区间比率变量的数值呈现连续标度。比如,我们对西班牙足球运动员的体重感兴趣,如果测量数值非常详细,比如 83.9 或 74.5 公斤,为每一个值绘制一个单独的柱形是没有意义的。相反,我们构建 区间 。
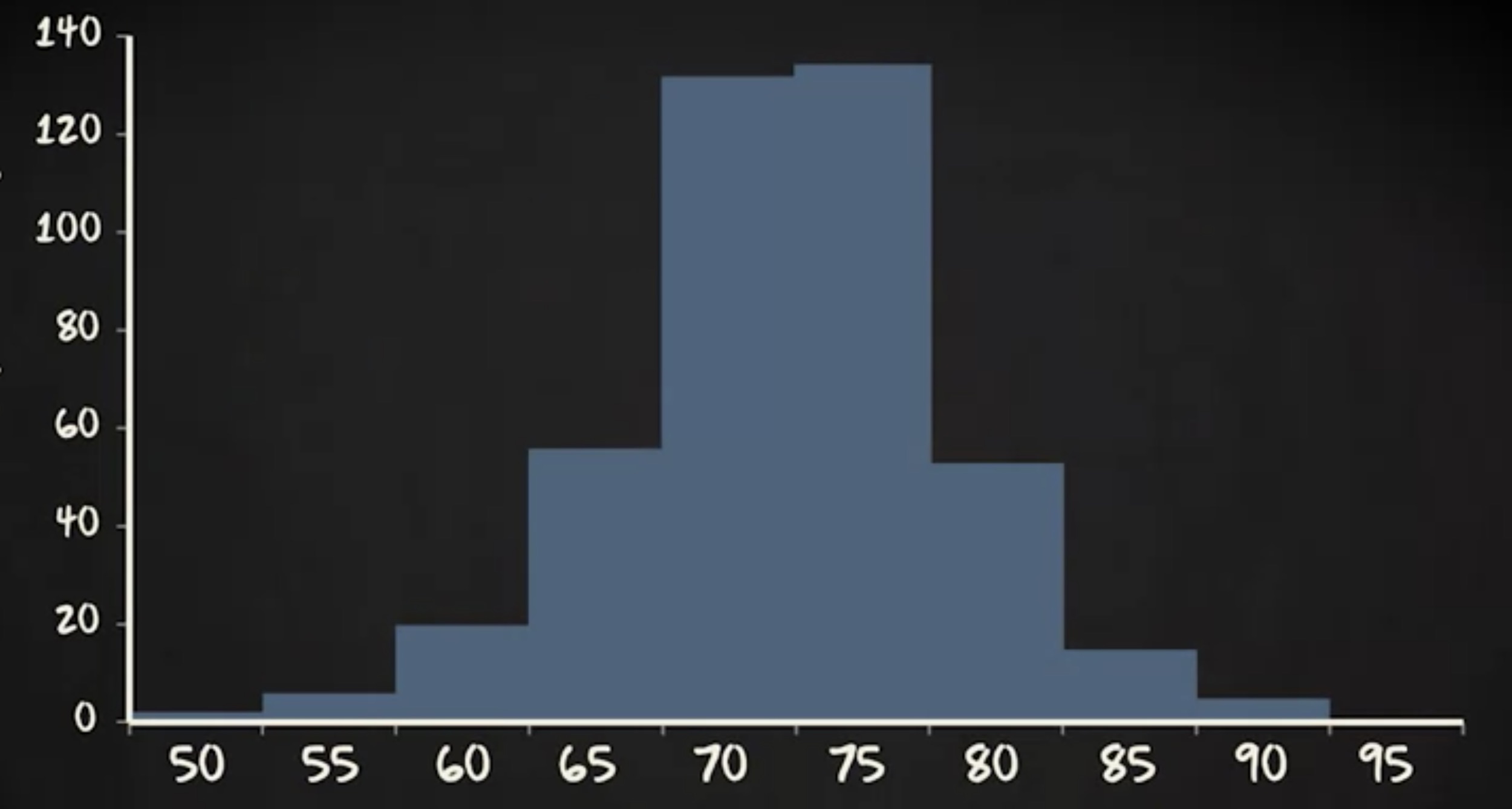
在此图中,有 10 个 区间,每个区间 5 公斤,第一个区间范围从 47.5 公斤到 52.5 公斤 显示 50 ,因为 50 是该区间的中间。对于创建的区间的数量,没有固定的规则。但是,重要的是区间数值必须相同,所以在此图中都是五公斤。可以一眼看出大多数球员的体重约为 75 公斤,还可以看到,重量小于 60 或大于 90 是非常罕见的。
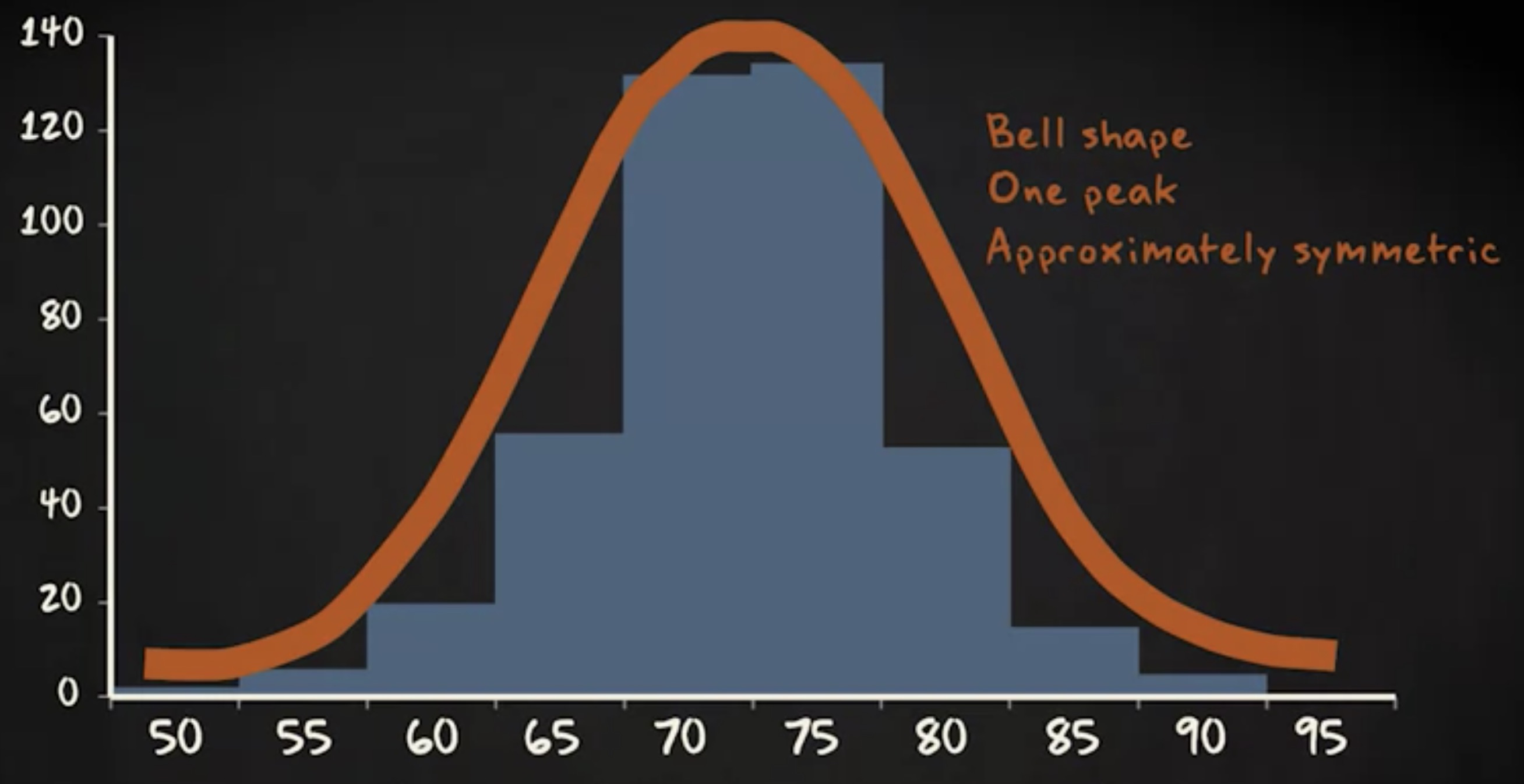
如图所见,此直方图具有特定形状,它是钟形的,有一个 峰值 且两侧近似对称。你会经常遇到钟形分布,但并非所有直方图都是钟形。
直方图也可以向左或向右 倾斜 。偏斜的直方图不是对称的,因为分布的一侧比另一侧延伸得更远。
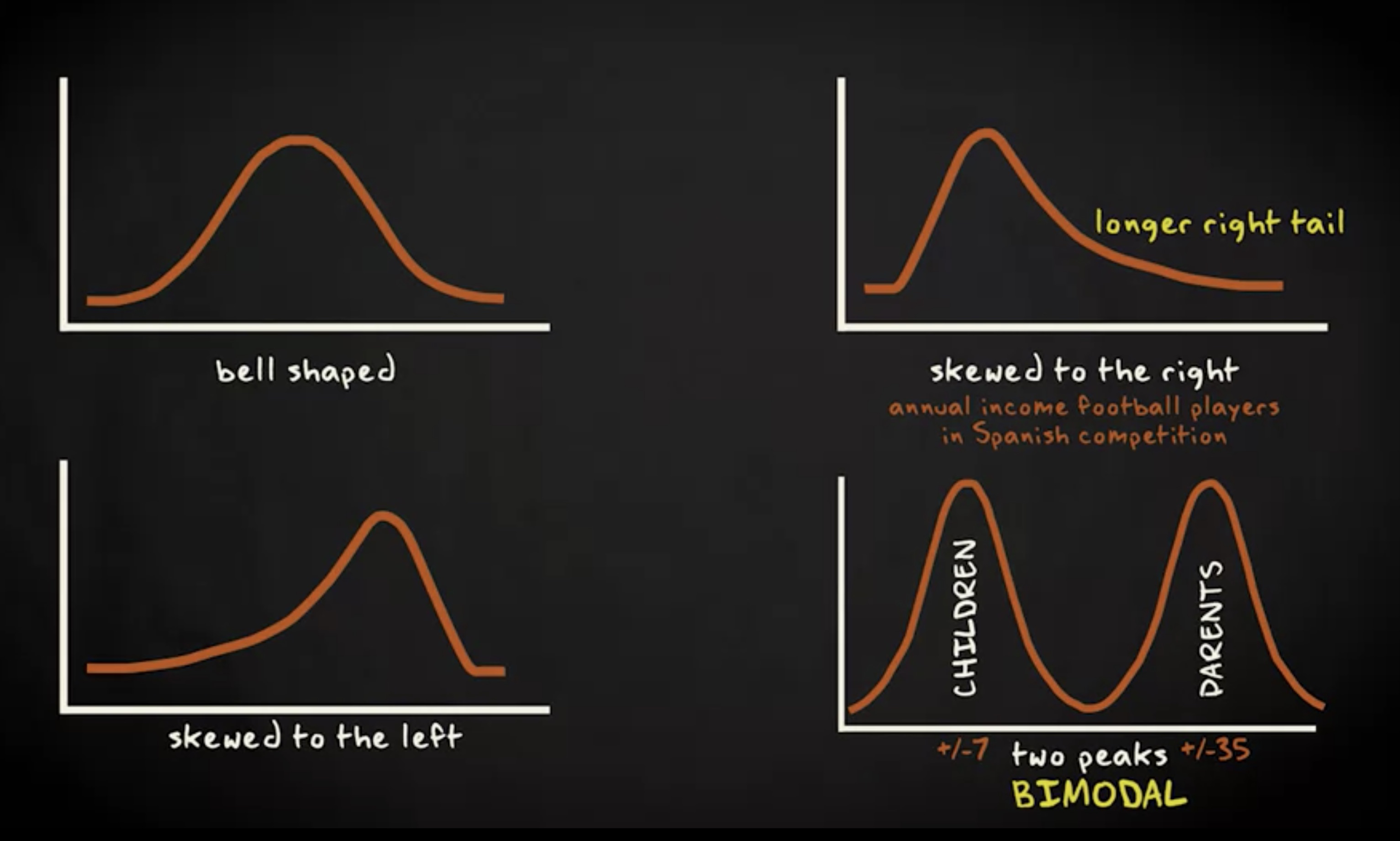
有的直方图向左倾斜,而有的直方图向右倾斜。向右倾斜的直方图变量是西班牙比赛中球员的年收入。与球员的平均收入相比,收入很少的球员不会很多。但是,也会有一些球员比大多数球员赚的多得多。因此,右尾更长。
直方图也可能有两个峰值:设想两队六到八岁球员之间的足球比赛。比赛结束后,所有的孩子和父母都去食堂喝东西。
你感兴趣的问题是,食堂里的人年龄如何分布。在这种情况下,年龄变量的直方图有两个峰值。毕竟,食堂里的孩子是 6 到 8 岁的孩子和他们的父母,他们最有可能在 30 到 40 岁之间。
因此,可能在 7 岁左右达到峰值,在 35 岁左右再达到峰值。我们说这个变量是双峰而不是单峰。
总结
这篇教程最重要的一个内容是:通过图表概述数据是一个好主意。如果处理定类或定序变量,你应该制作饼图或柱图。如果变量是定距或者定比变量,则应绘制直方图。 永远不要忘记查看变量的形状,它是钟形且对称的吗?它是单峰,还是双峰?分布是否倾斜? 评估分布的形状至关重要, 因为它可能影响你之后使用的统计方法。

