欢迎关注微信公众号「Swift 花园」
统计推断
这一节我们以睡眠为例。假设你通常每晚睡 8 个小时,你突然做了年轻爸爸或者年轻妈妈,你的睡眠时间减少到每晚 5 个小时,这意味着每晚减少 3 个小时,相当于每周 20 个小时,每年 1000 个小时,差不多 40 天。换言之,如果你家宝宝继续保持他 / 她的睡眠时间,一年之后你会比之前少睡 大约 40 天。
回到统计学,想象你想要知道你家乡的年轻父母在孩子刚出生那一年减少了多少睡眠。在这一节中我们将讨论统计推断。我们会基于样本信息,得出关于总体的结论。我们将会区分两种统计推断的方法,一种叫 统计估计 (statistical estimation) ,另一种叫 假设检验 (hypothesis testing) 。在这篇教程中,我们将先了解统计估计。
有两种方式估计总体参数的值,其一叫 点估计 (point estimate) ,它是一个对于总体参数的最佳猜想。其二是 区间估计 (interval estimate) ,它是一个我们预期参数会落在的范围。
想象我们抽取了 60 个受试者样本,有了第一个小孩后每晚减少的睡眠小时数均值为 2.6 小时。这个均值是一个对于总体均值很好的点估计。换言之,$ \bar x $ ,是一个对于 $ \mu $ 的很好的点估计。不过,单一的点估计无法告诉我们估计是否接近我们感兴趣的总体参数。因此,研究人员通常还希望知道点估计可能的准确度。他们借由计算区间估计来显示这种准确度。
区间估计是一个最有可能包含总体实际参数值的数字区间。基于我们的样本均值 2.6 小时,我们可以预测,比如说,你家乡新生儿父母每晚睡眠减少的平均小时数介于 2.3 小时到 2.9 小时之间。
这个区间包含总体参数值的概率,被我们称为 置信水平 (confidence level) ,置信水平总是一个接近 1 的值,多数情况下是 0.95 。接下来我们将讨论有 95% 置信水平的区间。
已知总体标准差,求均值的置信区间
假设我们知道 60 个年轻父母的样本在第一个小孩出生后睡眠减少小时数的标准差是 0.9 小时,也知道总体的标准差是 1.1 小时。(实践中,不太可能知道这个参数,但这里我们先假定你知道)
这一节中,我们将学习如何基于样本信息和总体的标准差来构造 置信区间 (confidence interval) 。首先,我们来解释一下这样一个置信区间应该如何解读。
为了构造一个置信区间,我们需要用到样本均值的抽样分布。毕竟,我们是在处理一个来自总体的样本。 我们知道,只要样本足够大,抽样分布就是正态分布的,并且均值等于总体的均值,标准差等于总体的标准差除以样本数 n 的平方根。我们还知道,找到距离样本均值少于等于两个标准差的概率是 0.95 。更精确的,如果查询对应概率的 z 分数,我们会得到 -1.96 和 1.96 。
这意味着我们有 95% 的机会令样本均值落在总体均值 1.96 个标准差范围内。 1.96 个标准差的距离我们称为 误差界限 (margin error) 。误差界限告诉我们用样本均值 $ \bar x $ 估计总体均值的准确程度。 95% 置信区间的公式如下:
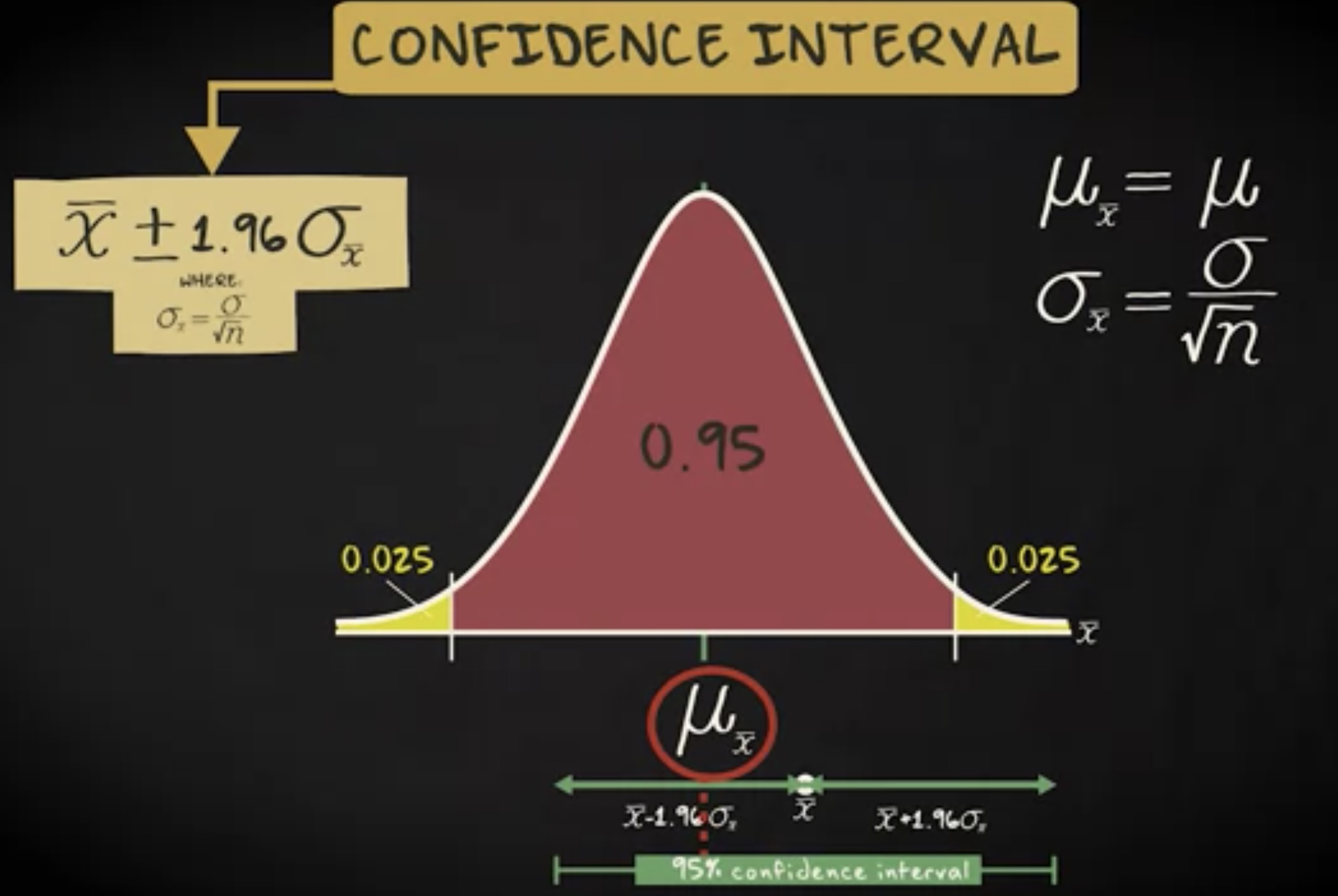
它是由点估计或者样本均值加减误差界限,即 1.96 个标准差。注意我们是在处理样本均值的抽样分布。因此分布的标准差等于 $ \frac {\sigma}{\sqrt {n}} $ 。接下来请集中注意力,因为过程会有点复杂。
假设你抽取一个样本,样本均值由某个点表示,从均值往两侧有一根线表示误差界限。它们一起构成了 95% 的置信区间。如果样本均值落在红色区域,则置信区间包含总体均值 $ \mu $ 。如果样本均值不落在红色区域,则置信区间不包含总体均值 $ \mu $ 。我们讨论的是 95% 的置信区间,这意味着随机选择一个样本,它包含总体均值的概率是 0.95 ,不包含总体均值的 0.05 。换言之,如果我们抽取无限多个样本, 95% 的情况,我们的置信区间会包含总体的均值。
现在让我们回到例子。例子中样本均值是 2.6 小时。总体标准差 1.1 。样本容量是 60 ,现在我们有了计算置信区间需要的全部数字。公式如下:
我们知道 $ \sigma_{\bar x} = \frac {\sigma}{\sqrt {n}} $ ,即 $ \frac {1.1}{\sqrt {60}} $ ,得到 0.142 。接下来计算误差界限, 1.96 乘以 0.142 ,约等于 0.28 。样本均值等于 2.6 ,因此 95% 置信区间是 2.6 减去 0.28 到 2.6 加上 0.28 的区间,即 2.32 到 2.88 。我们可以说,我们有 95% 的信心确定这个区间包含了实际的总体均值。更精确地说,如果我们从总体中抽取无限多个大小为 60 的样本,并且对于每个样本,我们计算误差界限, 95% 的情况下,总体的均值会落在样本的置信区间内。

如果新生儿父母的这种境况会持续一年,我们有 95% 的信息说,这些人会减少 2.32 乘以 365 小时到 2.88 乘以 365 小时的睡眠时间,或者说, 846.8 小时到 1,051.2 小时,又或者说, 35.3 到 43.8 个整天。
未知总体标准差,求均值的置信区间
95% 置信区间用于评估总体的均值,它告诉我们我们有 95% 的信息这个区间包含实际的总体均值。利用这个公式 $ \sigma_{\bar x} = \frac {\sigma}{\sqrt {n}} $ ,你可以计算区间的两个端点。这个公式有一个问题,为了计算置信区间,你需要知道总体的标准差。然而,我们通常并不知道这个参数。毕竟,我们本来就在用样本推测总体的参数。
这一节中,我们将学习如何在不知道总体参数的情况下做出推断。解决方案是我们估计总体的标准差,因而我们要引入另一个分布,它叫 T 分布 。让我来告诉它如何工作。
想象我们问了 60 个年轻家庭他们在有了第一个孩子之后睡眠时间少了多少个小时,均值是 2.6 小时,标准差是 0.9 小时。为了构建一个 95% 的置信区间,我们需要用到 $\bar x\pm1.96 \sigma{\bar x}$ ,
或者可以写成 $\bar x\pm {Z{95 \%}} \sigma_{\bar x}$ 。这一次,我们不知道总体的标准差。

因此我们用样本的标准差来估计总体的标准差,公式变成: $\bar x\pm {Z_{95 \%}} s_e$ ,其中 $ s_e = \frac {s}{\sqrt {n}} $

我们把 $ se $ 这个估计的抽样分布的标准差称为 标准误差 (standard error) 。但是因为我们现在是估计标准差,所以我们在计算中引入了额外的误差。基于此,我们引入另一个分布, z 分布。由于额外的误差,我们现在使用 T 分布,公式如下。
$\bar x\pm {t_{95 \%}} se$
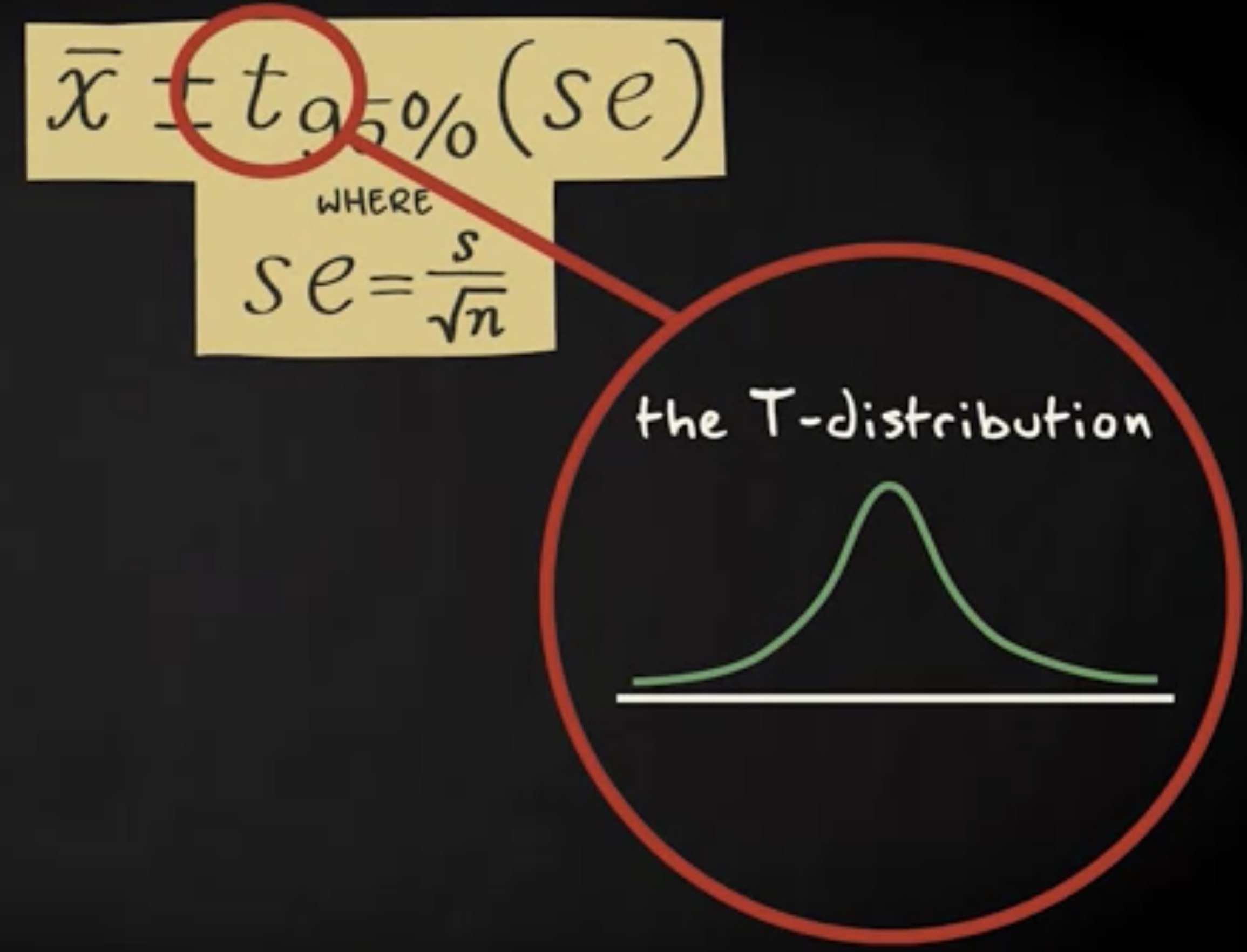
现在让我来详细解释 t 分布和 t 分数。 t 分布跟标准正态分布非常之相似,它是钟形的,对称的,并且均值是 0 。但是,它有一点点区别。 因为我们现在是估计抽样分布的标准差,我们引入了额外的误差。当我们的样本比较小时,这个误差很可观。 t 分布将这小样本的这个误差考虑在内了,因此它比标准正态分布稍微宽一点,标准差更大一些。如下:
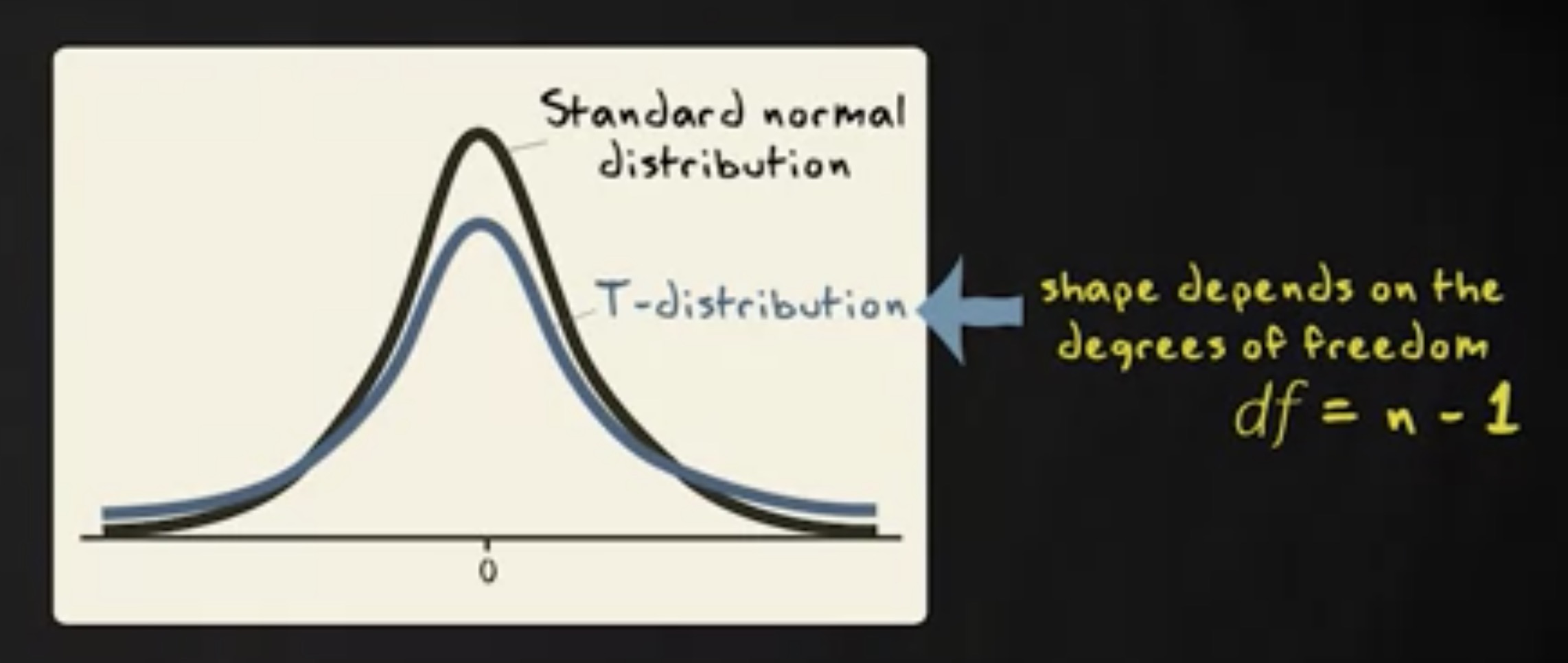
黑色的分布是标准正态分布,蓝色的分布是 t 分布。 t 分布的准确形状取决于样本容量。样本越大,t 分布越接近标准正态分布。更准确的说, t 分布的形状取决于单一个参数,我们称为 自由度 (degrees of freedom) ,以 $ df $ 注记。 t 分布中的自由度等于样本容量 n - 1 。这意味着我们实际上有许多不同的 t 分布,每一个都有单独的 $ df $。比如,自由度为 2 的 t 分布:
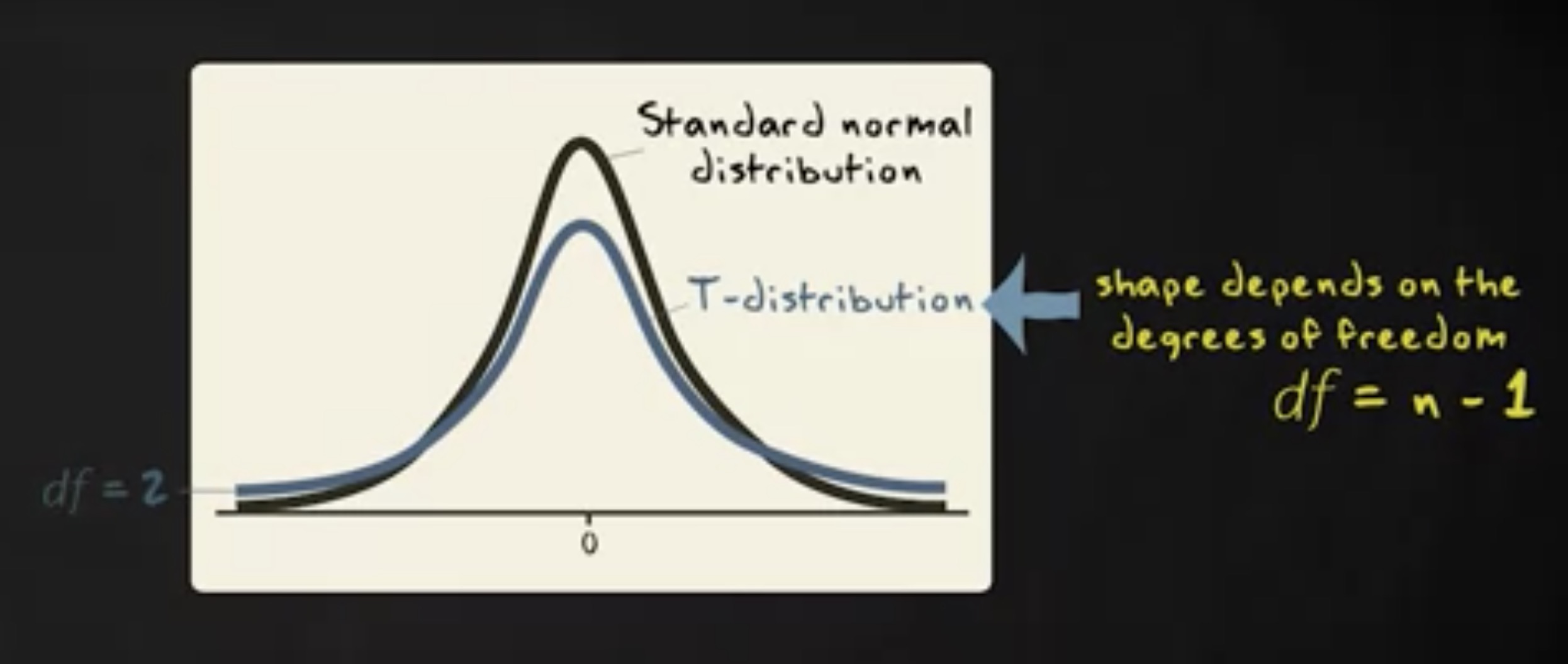
自由度为 5 的 t 分布:
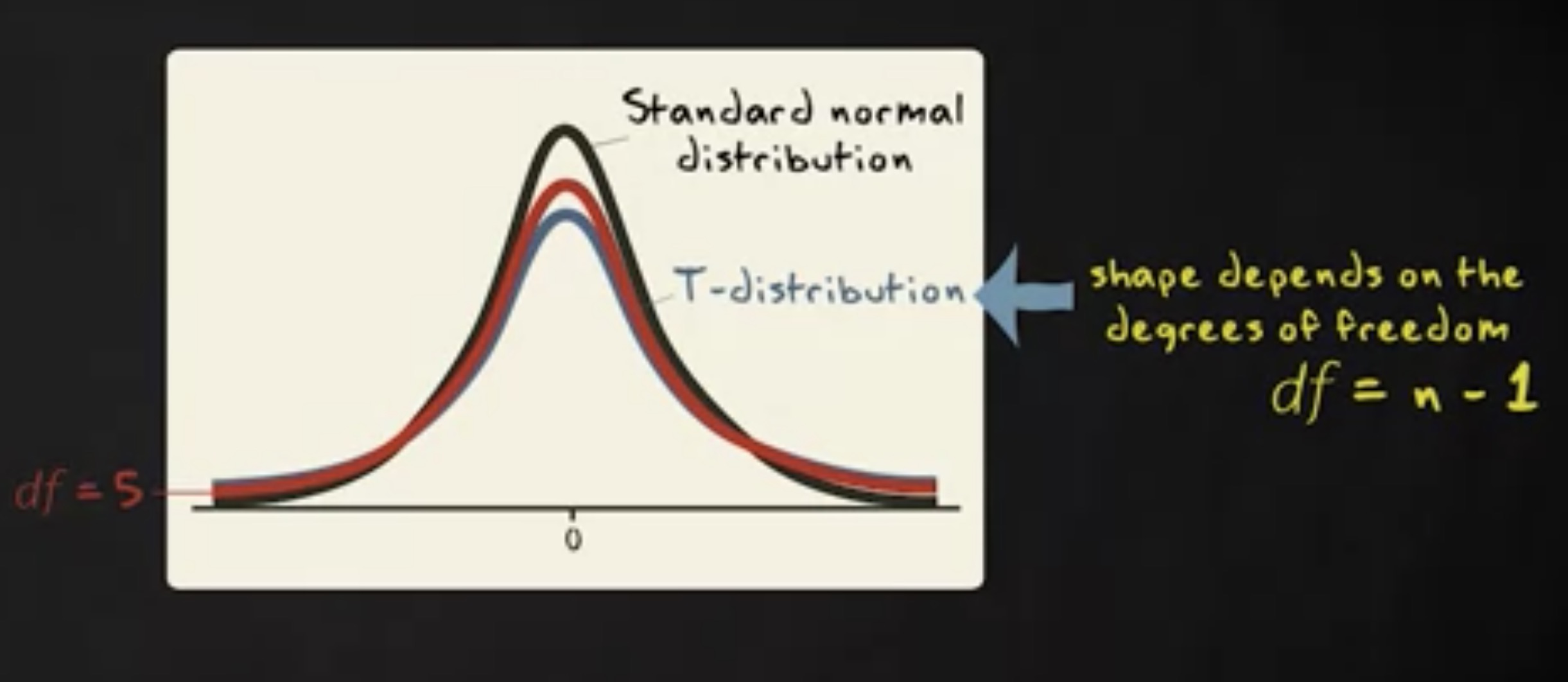
自由度为 30 的 t 分布:
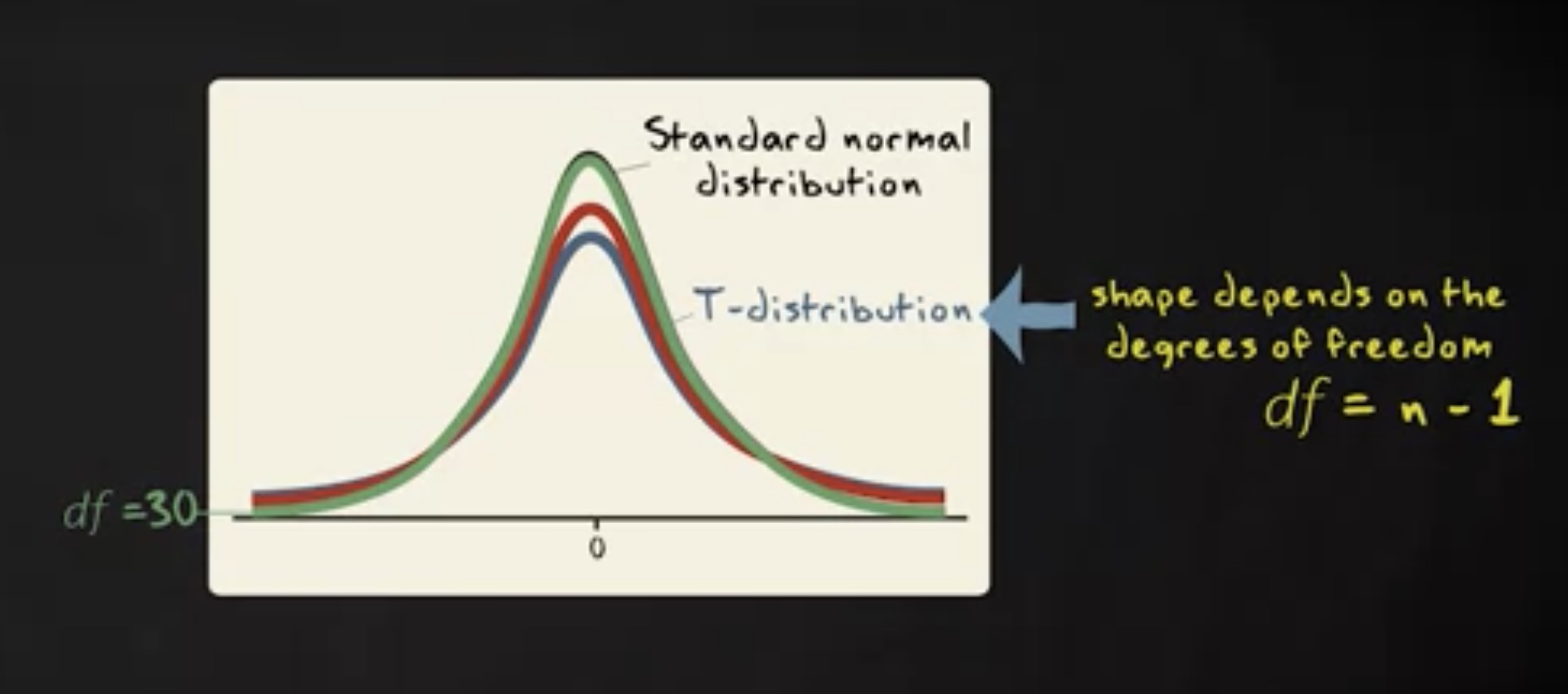
可以看到,当我们有 30 或者更大自由度时, t 分布几乎就等同于标准正态分布。更准确的说,标准正态分布其实就是自由度等于无限的 t 分布。
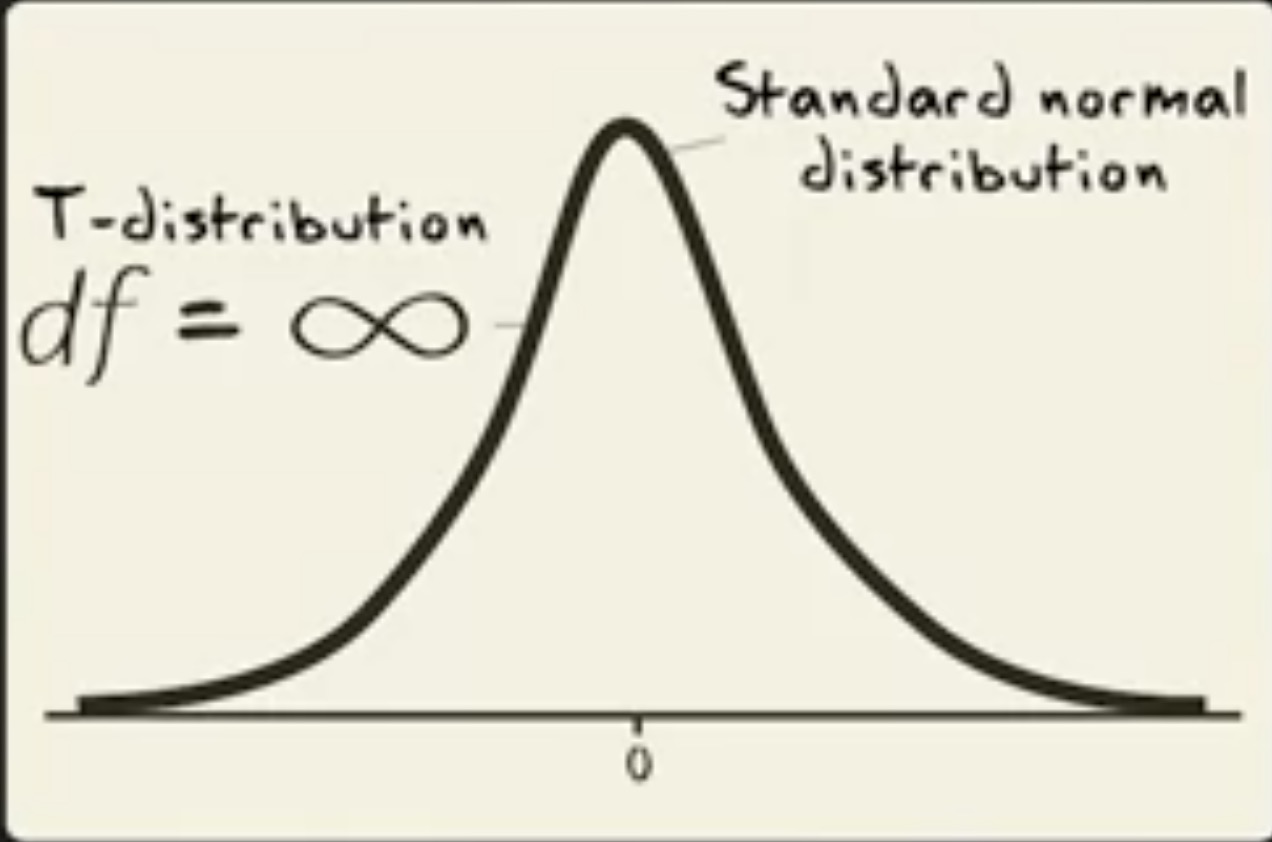
同标准正态分布和 z 分数一样,我们也可以为特定的 t 分数寻找累积概率。重要的区别在于,这些概率依赖于自由度。当你计算一个 95% 置信区间时,你可以为所有可能的自由度找到对应 95% 置信水平的 t 分数,这个表格称为 t 表格 ,它和 z 表格类似。
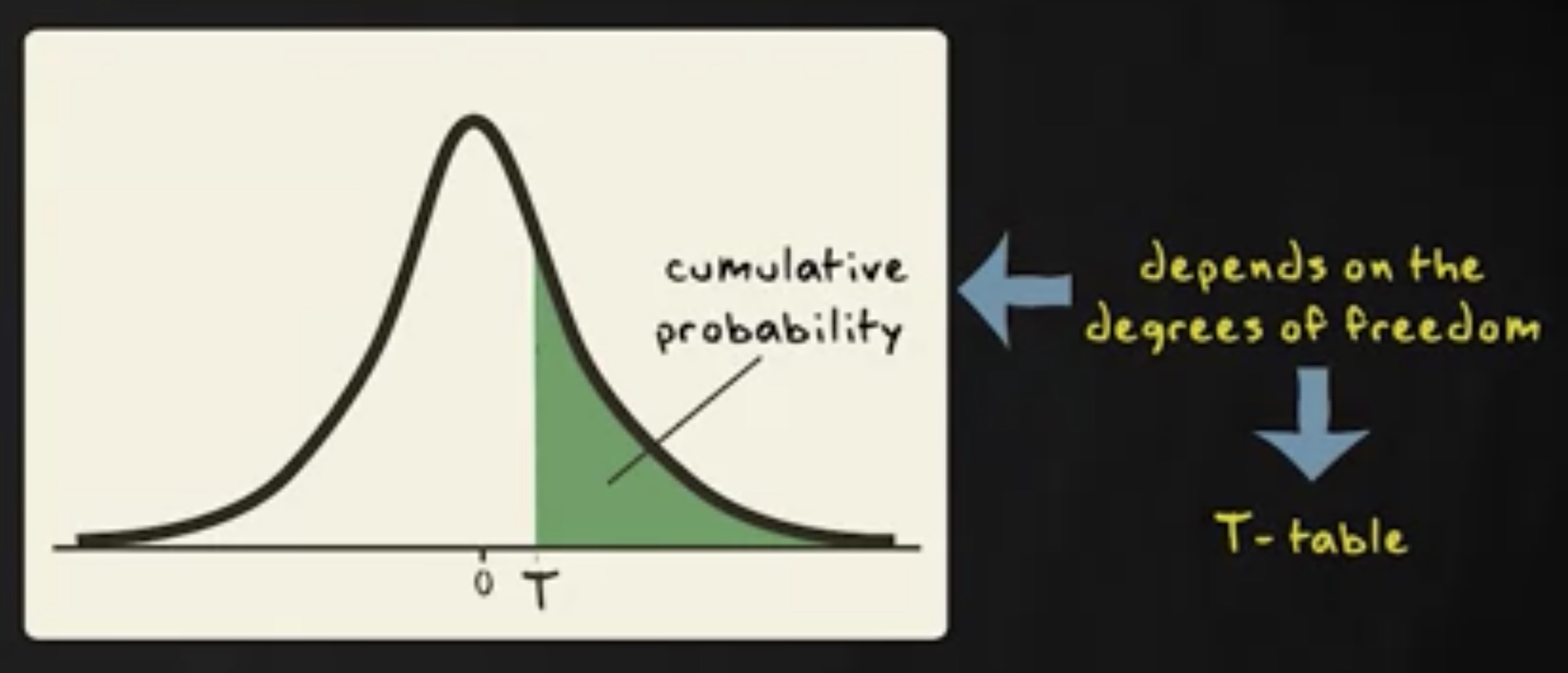
让我用睡眠时间的例子来演示。样本中睡眠减少小时数的均值是 2.6 小时,标准差是 0.9 小时,样本容量是 60 。计算 95% 置信区间的公式:
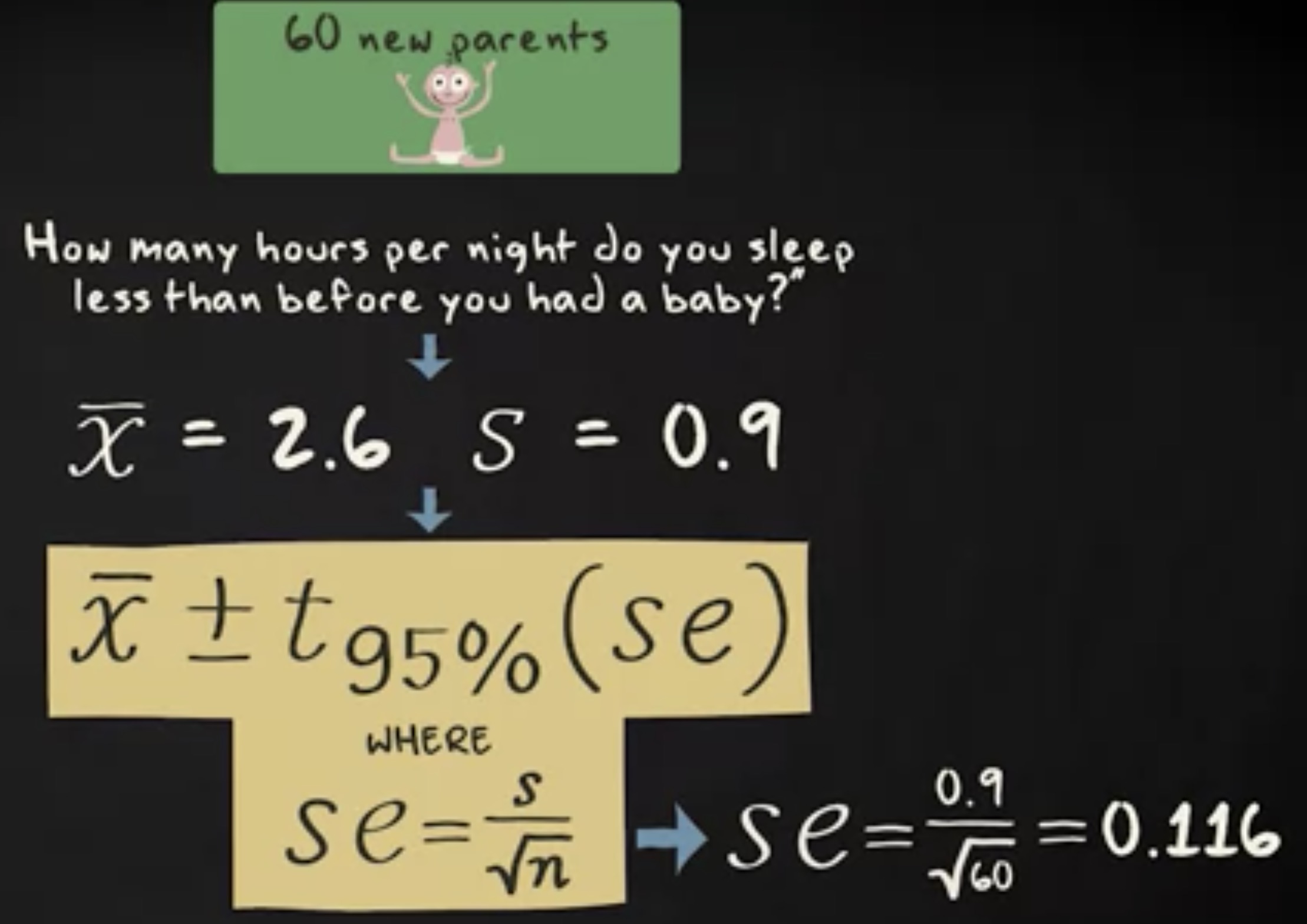
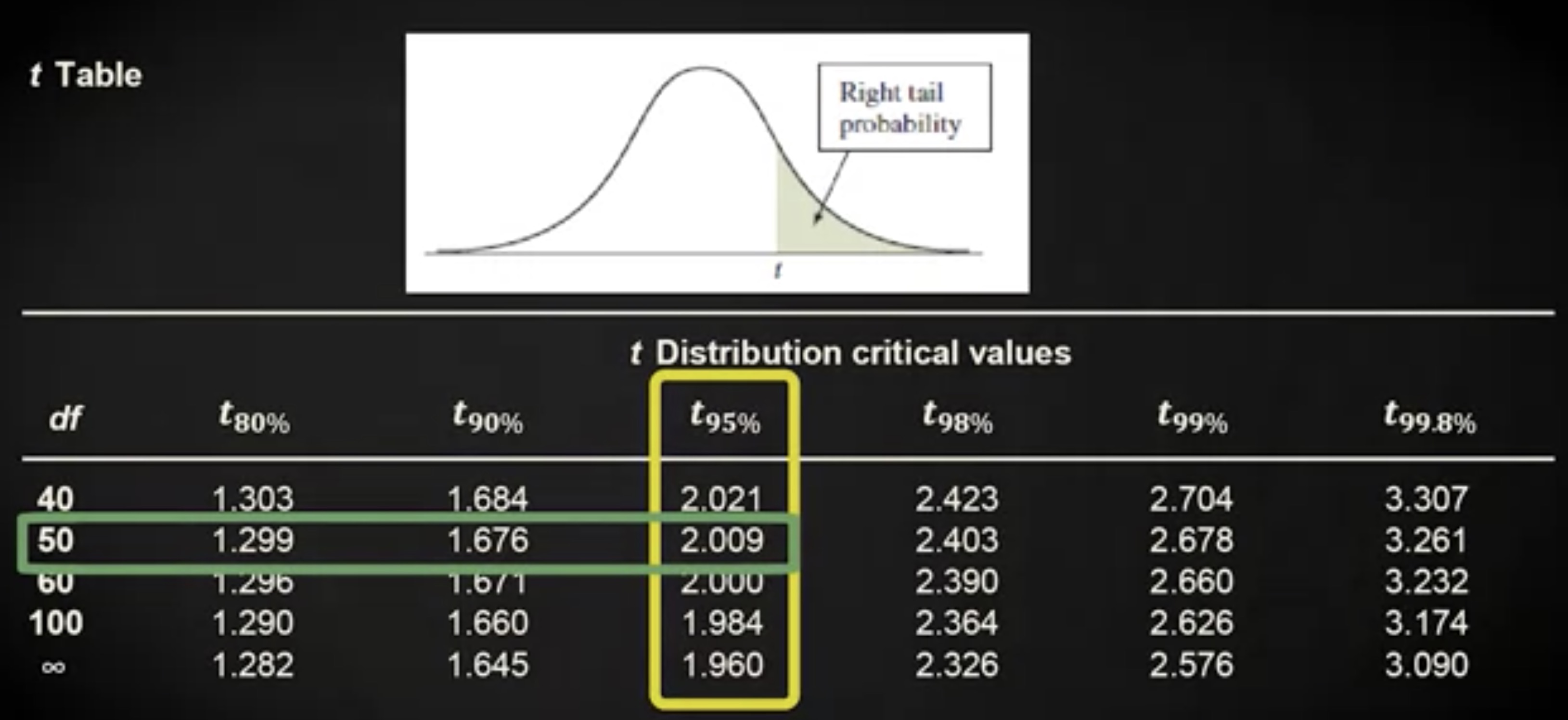
让我们从标准误差开始,它等于样本标准差除以 n 的平方根,即 0.9 除以 60 的平方根,得到 0.116 。我们的标准误差,或者说,估计的样本均值的抽样分布的标准差等于 0.116 。为了计算误差界限,我们需要用标准误差乘以 95% 置信区间的 t 分数。如你所知, t 分数取决于自由度。自由度 df 等于 n - 1 。我们有 60 个样本,因此 60-1 的 50 。在 t 表格中,我们在列中查找 95% 置信水平,在行中查找 59 自由度。因为表格中没有报告 59 自由度,我们向下取 50 自由度。对应的 t 分数是 2.009 。
因此我们用 0.116 乘以 2.009 ,大约 0.23 。从样本均值 2.6 中加减这个值后,得到我们的置信区间是 2.37 到 2.83 。我们有 95% 的信心认为这个区间包含实际的总体均值。
为了计算总体均值的置信区间,有两个假定需要满足。首先,你的数据是随机获取的。换言之,样本必须是随机样本,否则你的发现就不是合法的。其次,总体必须近似正态分布。这一点可能是个问题,因为总体中的许多变量可能并不是正态分布的。不过,好消息是,采用 t 分布来构造置信区间,可以有效对抗第二个假设破坏。也就是说,即使违反了假设,这种统计方法仍然是健壮的。最后,在基于 t 分布构造置信区间是,你还需要对异常值保持机警。如果数据里有异常值,那么这个方法可能会失效。因此要记得在开始之前检查数据。

