欢迎关注微信公众号「Swift 花园」
众数、中位数和平均数
在前一篇教程中,我们学会通过图表概述分布。这同样适用于描述分布的中心位置,有三种主要方式,它们分别是:众数 (mode) ,中位数 (median) 和 平均数 (mean) 。
这三个 m 通常被称为集中趋势的度量。
找到众数很容易,它是出现频次最高的值。 换句话说,就是最常见的结果。
如果测量定类或定序变量,众数通常用作衡量集中趋势。
在下面这个饼图中,可以看到西班牙主要球赛中球员来自哪些大洲。
饼图使众数一目了然,是欧洲 70% 的球员来自欧洲
这里的众数是欧洲 ,是最常出现的类别的名称,但众数不是 70% 。这只是该特定类别的观测百分比。可能有多个众数。试想有一个足球运动员,拥有十分分裂的球迷,其中一些觉得他非常和善,而另一些则认为他非常蛮横。来给这个球员起个名,Franco Galton。
试想你选取西班牙 500 名受访者作为代表样本,询问他们对 Franco Galton 的看法,受访者可以在 0 到 10 的范围内表明他们认为他的和善程度。 0 表示非常蛮横, 10 表示非常和善。
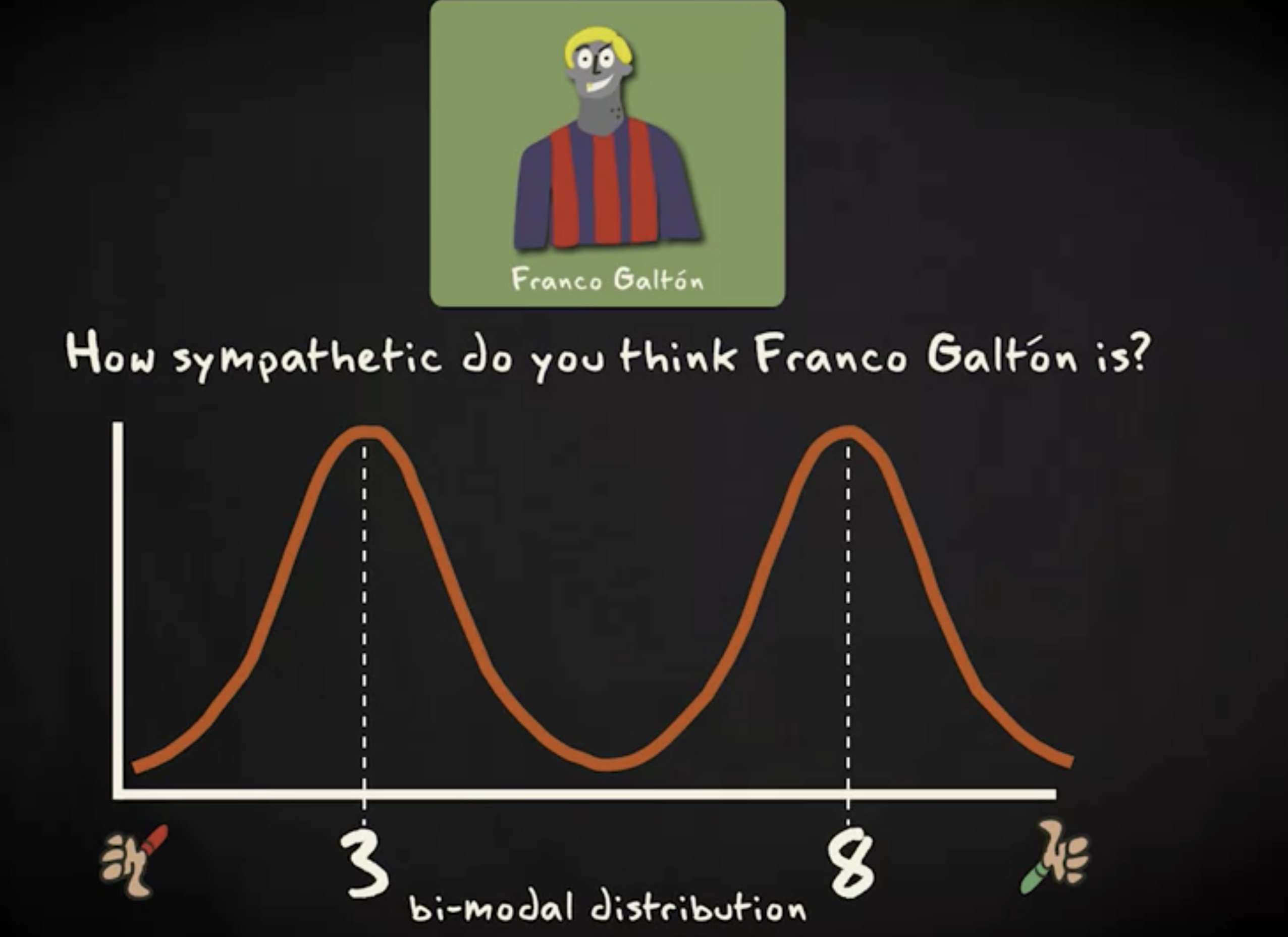
假设这是本研究得出的直方图形状,可以看到西班牙人分歧很大,有些人觉得 Galton 非常和善,有些人觉得他非常蛮横。正如所见,分布有 两个众数,即 3 和 8 这显然是双众数分布。
集中趋势的第二个衡量指标是中位数:观测值从最小到最大排序时,中位数就是观测值的中间值。
试想你还问了七位受访者,对另一著名球员 Tomas Bayez 的看法。假设这是他的研究数据矩阵,这里的众数是 8 ,是频次最高的值。
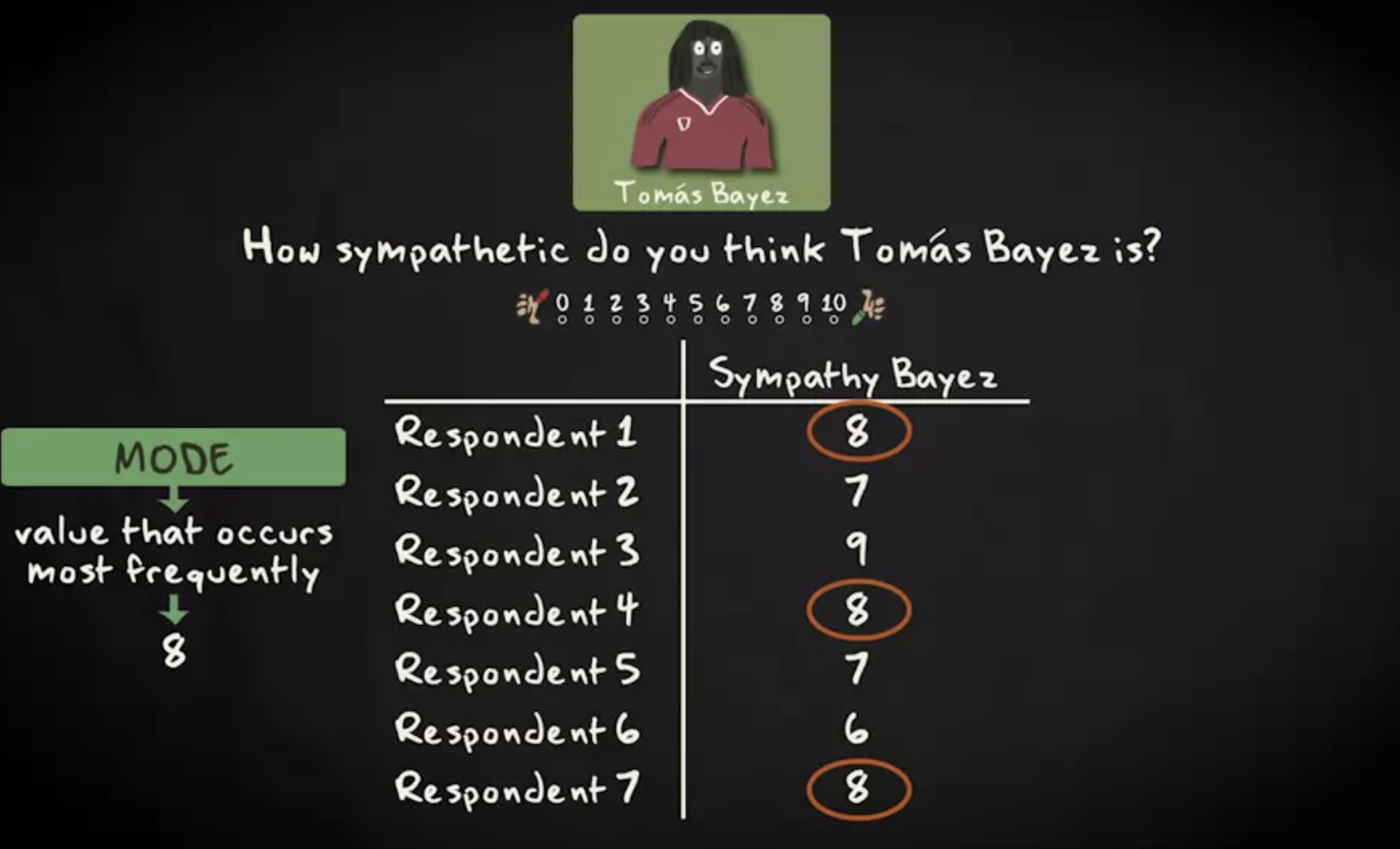
要计算中位数,首先必须将所有数值从低到高排序,然后选择中间值。所以这里的中位数是 8 。如果案例是偶数而非奇数,那就稍微复杂点了。试想受访者是 8 人,他们对 Tomas Bayez 的看法。

数值是从低到高排列的。但是,在这种情况下,没有单个中间值。该如何解决这个问题呢?我们取两个中间数值的平均值 7 和 8 相加除以 2 等于 7.5 。因此,中位数是 7.5 。请注意,中位数将分布分为两个相等的部分。 50% 的值低于中位数, 50% 的值高于中位数。
集中趋势的第三个衡量指标,是最常用的一个,也可能是你已经非常熟悉的,就是平均数。
平均数是所有观测值之和除以观测个数。
上面是用于计算平均值的公式。它看起来比较复杂,公式的含义是: x 横线表示变量 x 的平均数,等于 x 的总和除以样本个数,由 n 表示。
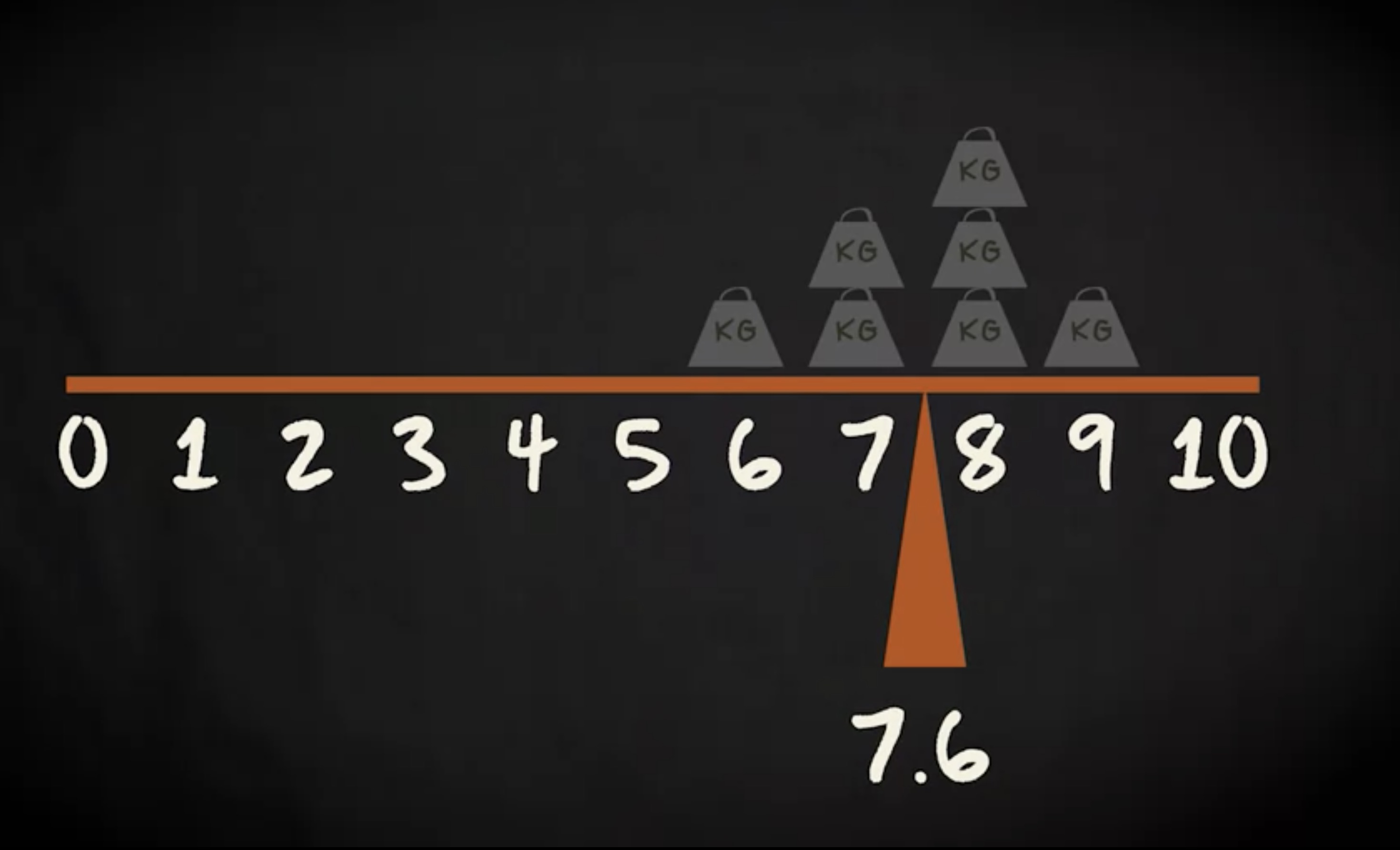
举个例子,借用 Tomas Bayez 的研究。公式告诉我们首先求总和, 6 加 7 ,加 7 ,加 8 ,加 8 ,加 8 ,加 9 ,等于 53 ,现在再除以 n 。样本量是 7 ,因此 53 除以 7 等于 7.6 平均数是 7.6 。

可以将平均数视为数据的平衡点。试想我们将重量平衡放置,那么平均数就是天平中心点。其中一侧的总重量恰好等于另一侧。
现在大家已经熟悉了这三个 m 。可以通过各种方式轻松计算一组数字的中间值,但报告时,该使用哪种中心趋势呢?
这部分取决于变量的测量级别。 如果是定类测量,则无法计算中位数或平均数,因为我们无法对定类变量进行数值运算,也不能对它们进行排序。当变量是定类变量时 唯一适合的集中趋势度量是众数。
如果是定量变量该怎么办呢?
试想你在家乡足球俱乐部的一个食堂里,你想计算所有在场人士的平均收入和中位收入,包括你自己,其他 5 位客人和吧员。

这是数据矩阵,平均数约为 35,000 ,中位数恰好是 35,000 , 它们彼此非常接近。使用哪一个来描述分布中心都无所谓。但现在,著名足球运动员 Franco Galton 走进食堂,比如他每年收入大约 7000 万 ,这时中位数略微增加到 36,000 ,然而,平均数却超过 800 万。
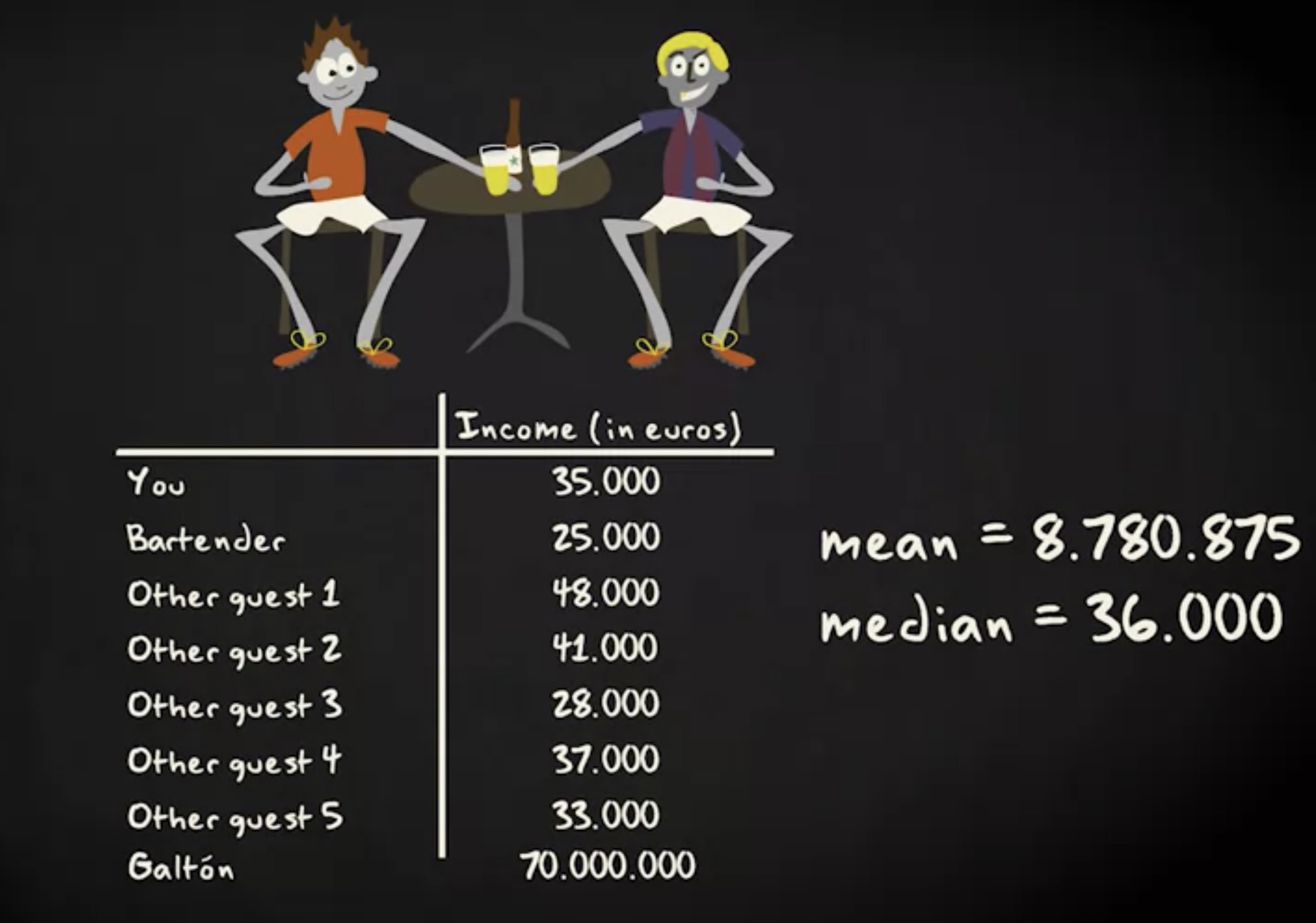
我们说 Franco Galton 是这个分布的异常值。他的收入远高于其他所有人,他的收入对平均收入产生不成比例的影响。在这种情况下,计算中位数描述分布中心比平均数更合理。
小结
描述分布中心可以使用三种方法:众数,中位数和平均数。如果变量是定类的,则使用众数;如果是定量的,则使用中位数或平均数 —— 如果有异常值或分布高度偏离,使用中位数。如果不是,那就使用平均数。
全距、四分位距和箱线图
你可能已经注意到了,纹身在足球运动员中越来越受欢迎。特别是所谓的纹身袖在球场上正在兴起。纹身袖,正如其名,是指满胳膊的纹身。
你对球员纹身占身体的比例感兴趣吗?
试想有两支球队,这里看到的是点图,表示两队中纹身占身体的百分比变量分布。水平线代表这个变量,原点代表每个团队中的 11 个人。
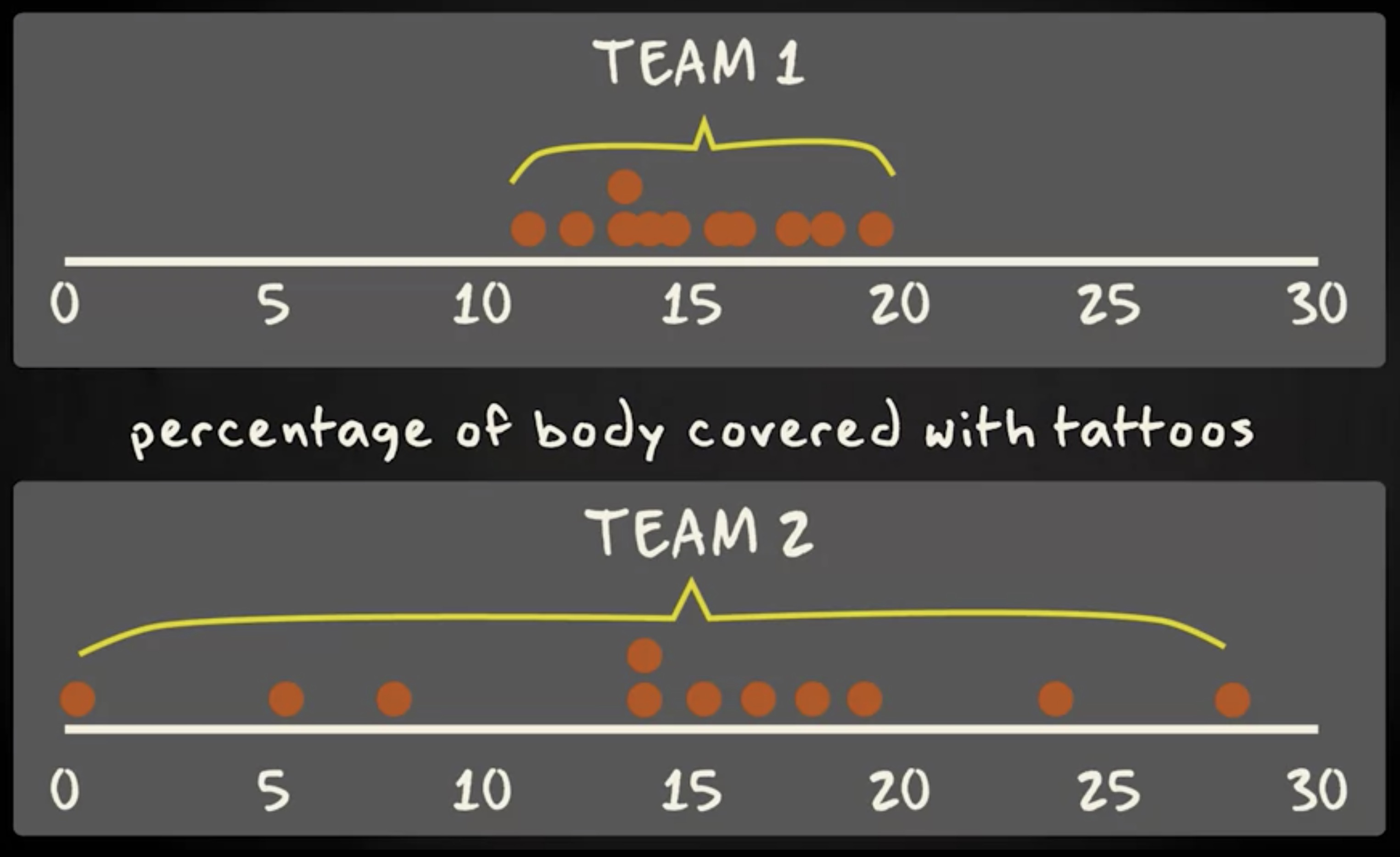
第一队队员纹身占比大约是 10% 到 20% 之间。在第二支球队中,球员的纹身占比差异很大,百分比范围是 0% 到大约 30% 之间。因此,这个团队彼此差异很大。但是两队众数,中位数和平均数却相同。两队的众数都是 14.1 ,中位数和平均数都是 15 。这表明为了充分描述分布,我们需要集中趋势度量之外的信息。 这一节我将向大家展示我们还需要了解有关数据变化或离散的信息,讨论两种变异性测量,即:全距 和 四分位距 ,还将讨论所谓的 箱线图 —— 这是一个非常有用的图表,可以很好地呈现分布中的数值如何离散。
全距是最简单的变异性度量:它是 最高值和最低值之间的差值 。
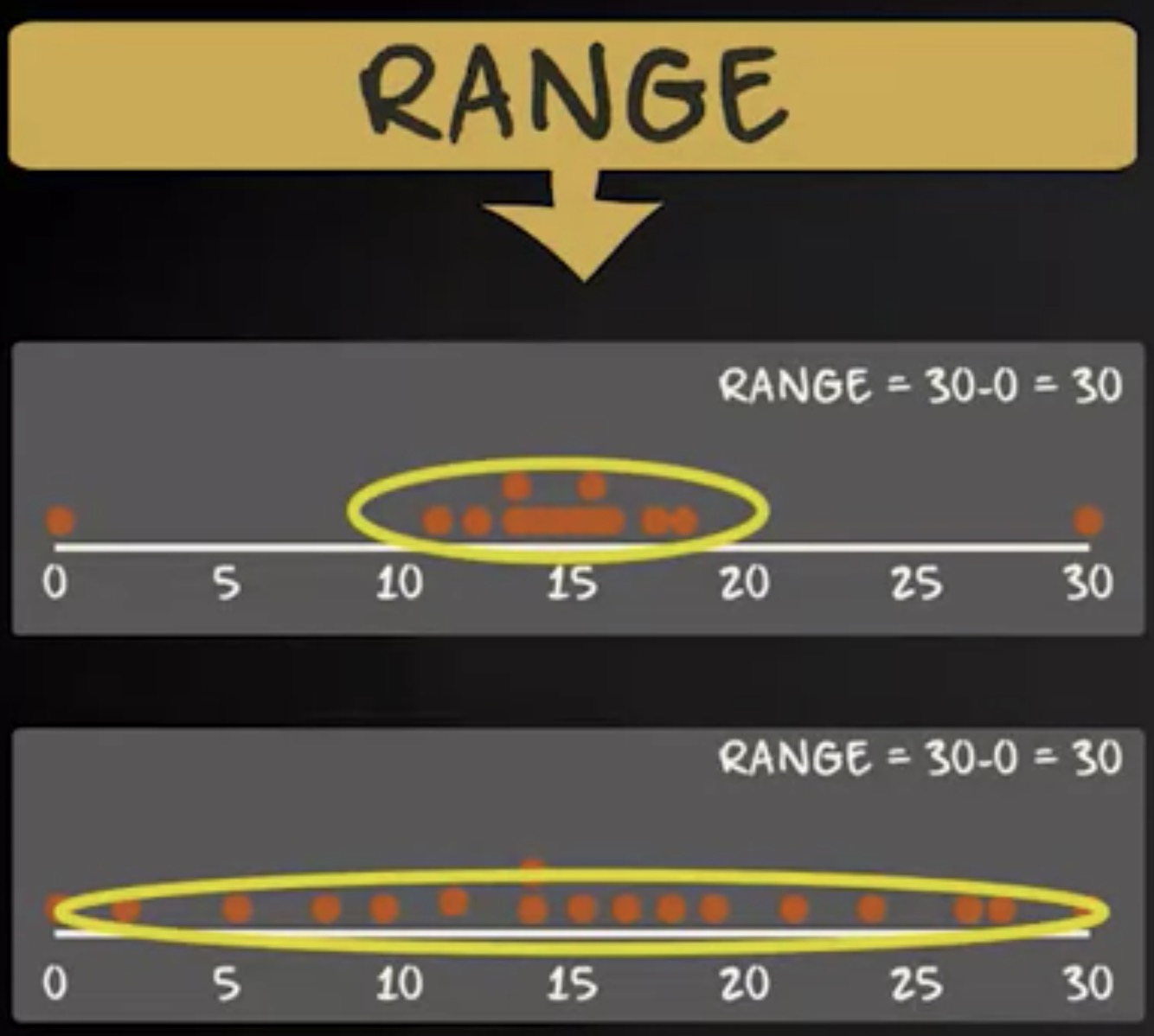
再来看看我们的两支球队:第一队的球员中最大纹身占比是 19.3% , 占比最小的是 10.8% ,范围是 19.3 减去 10.8 等于 8.5 ;第二队的球员中最大纹身占比是 27.7% ,占比最小的是 0% 。因此,范围是 27.7 减去 0 等于 27.7 。这清晰地显示第二队的变化范围比第一队的变化范围更大。全距是易于理解且易于计算的变异性度量。但是,在许多情况下,它并没有很好地呈现数据的变异性。 原因是它只考虑了极值。。 看看这两个分布,它们的范围相同,但一目了然第二个分布的变异性与第一个非常不同。
另一个更好的测量变异性的方法是 四分位距 ,因为它省略了极值,它将分布分为四个相等的部分。因此,如果分布看起来是这样的。
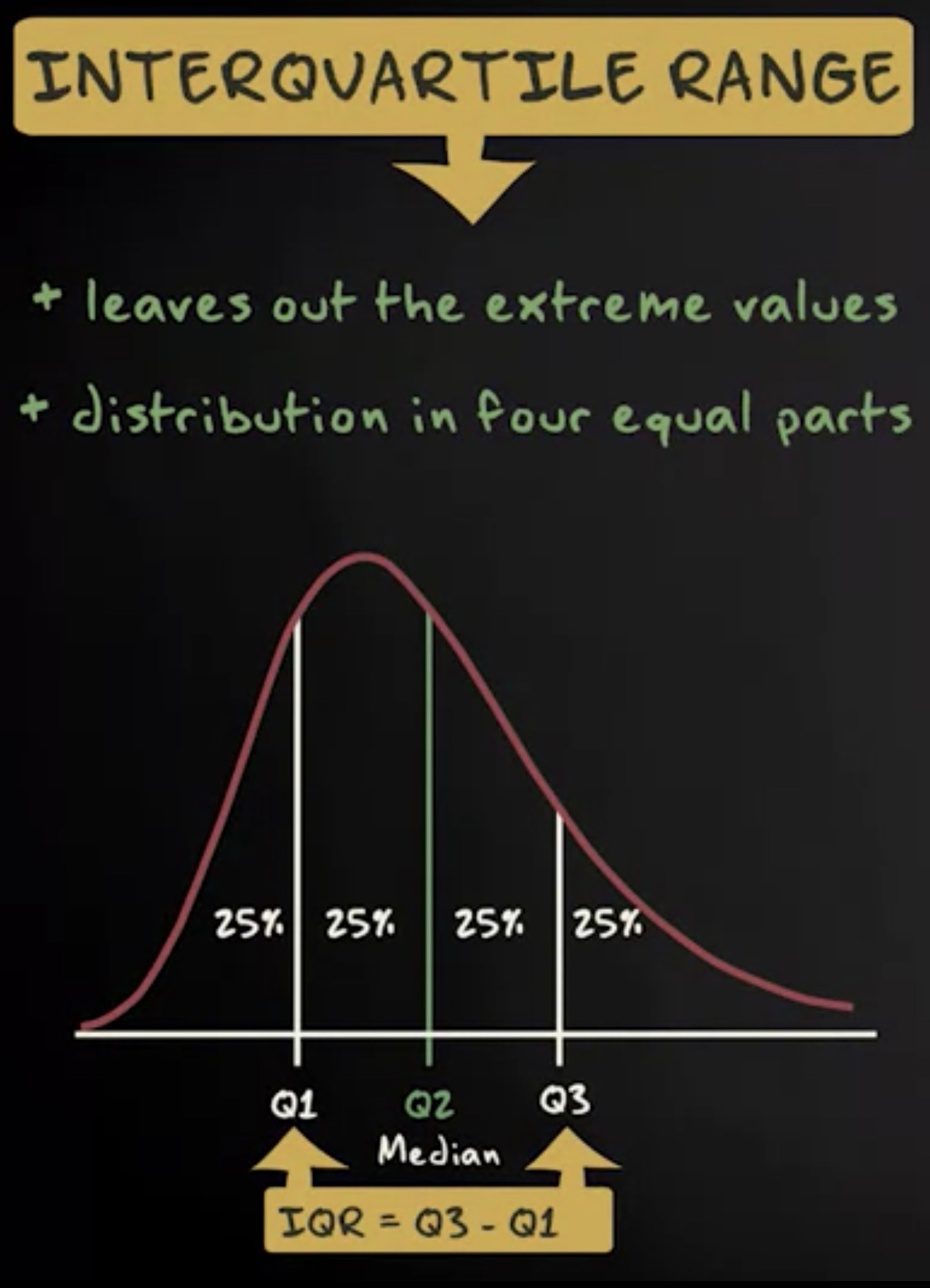
可以这样切分,将得分最低的 25% 划为一组,得分最高的 25% 划为一组,中间的两个 25% 再分两组。
这种划分分布方式称为四分位距,一共有三个 四分位 ,以下称为 Q1 , Q2 , Q3 。
如你所见,第二个四分位 Q2 将分布分为两个相等的部分。毕竟, 50% 的值低于该值, 50% 高于该值。
因此 Q2 与中位数相同。 四分位距是第三和第一个四分位之间的距离。换句话说,四分位距是 Q3 减去 Q1 。下面让我通过纹身占比来展示计算过程。
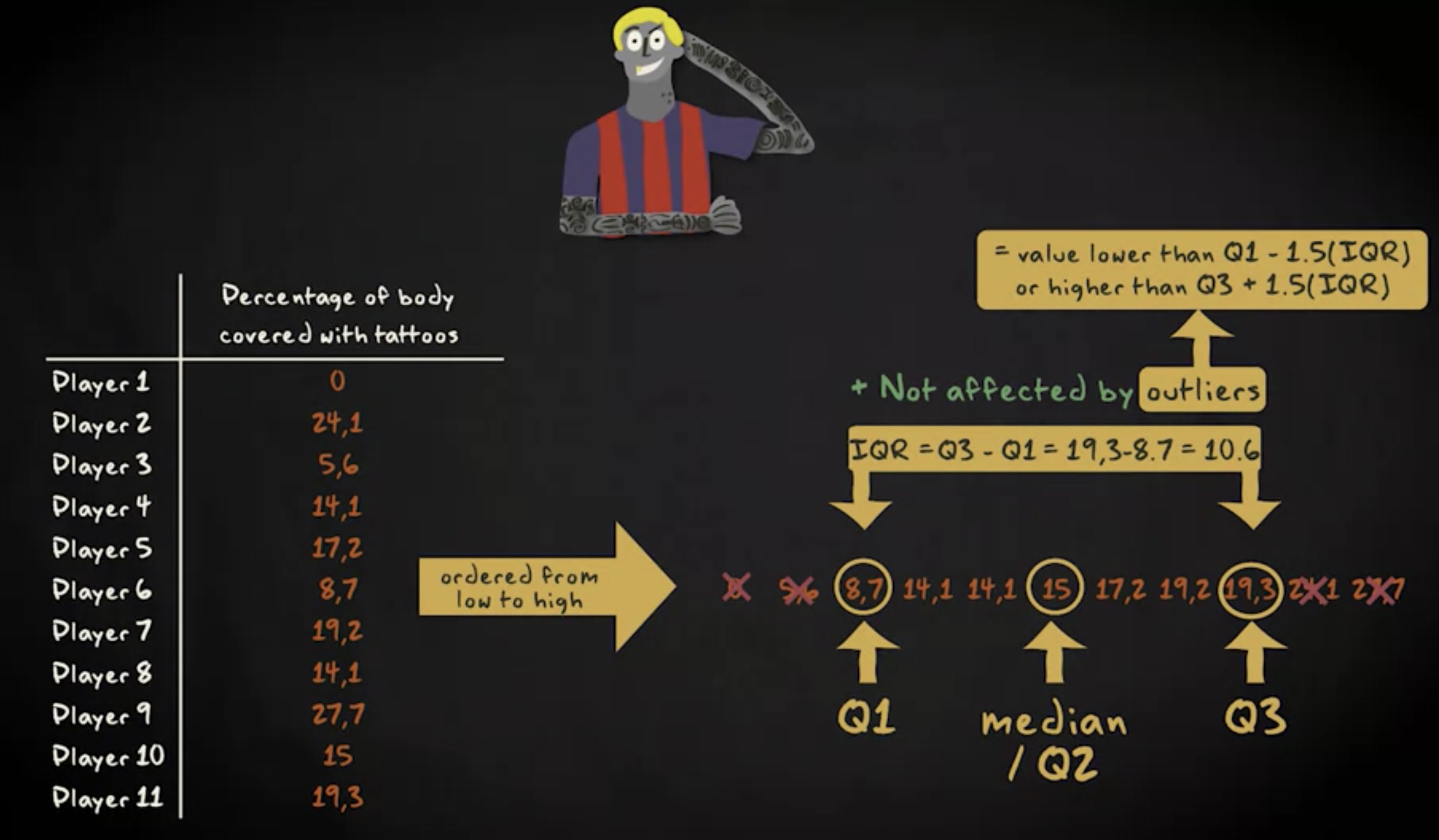
这是第二队的分布情况。首先,寻找中位数或者换句话说 Q2 。这很简单,中间数值是 15 ;可以通过查找中位数左侧数值的中间值找到 Q1 ,是 8.7 ;可以通过相同的策略在右侧找到 Q3 是 19.3 。现在,四分位距是 Q3 减去 Q1 即 19.3 减去 8.7 等于 10.6 。四分位距的主要优点是它不受异常值的影响,因为它没有考虑低于 Q1 或高于 Q3 的观测值。然而,在研究中寻找潜在的异常值可能仍然有用。 根据经验,如果观测值低于第一个四分位 1.5 个四分位距或高于第三个四分位 1.5 个四分位距则为异常值。
在描述中心和变异性以及检测异常值时,有一种特定类型的图非常有用,该图称为 箱线图 。
Q1,Q2 和 Q3 在箱形图中一目了然,最小值不是异常值,最大值不是异常值。
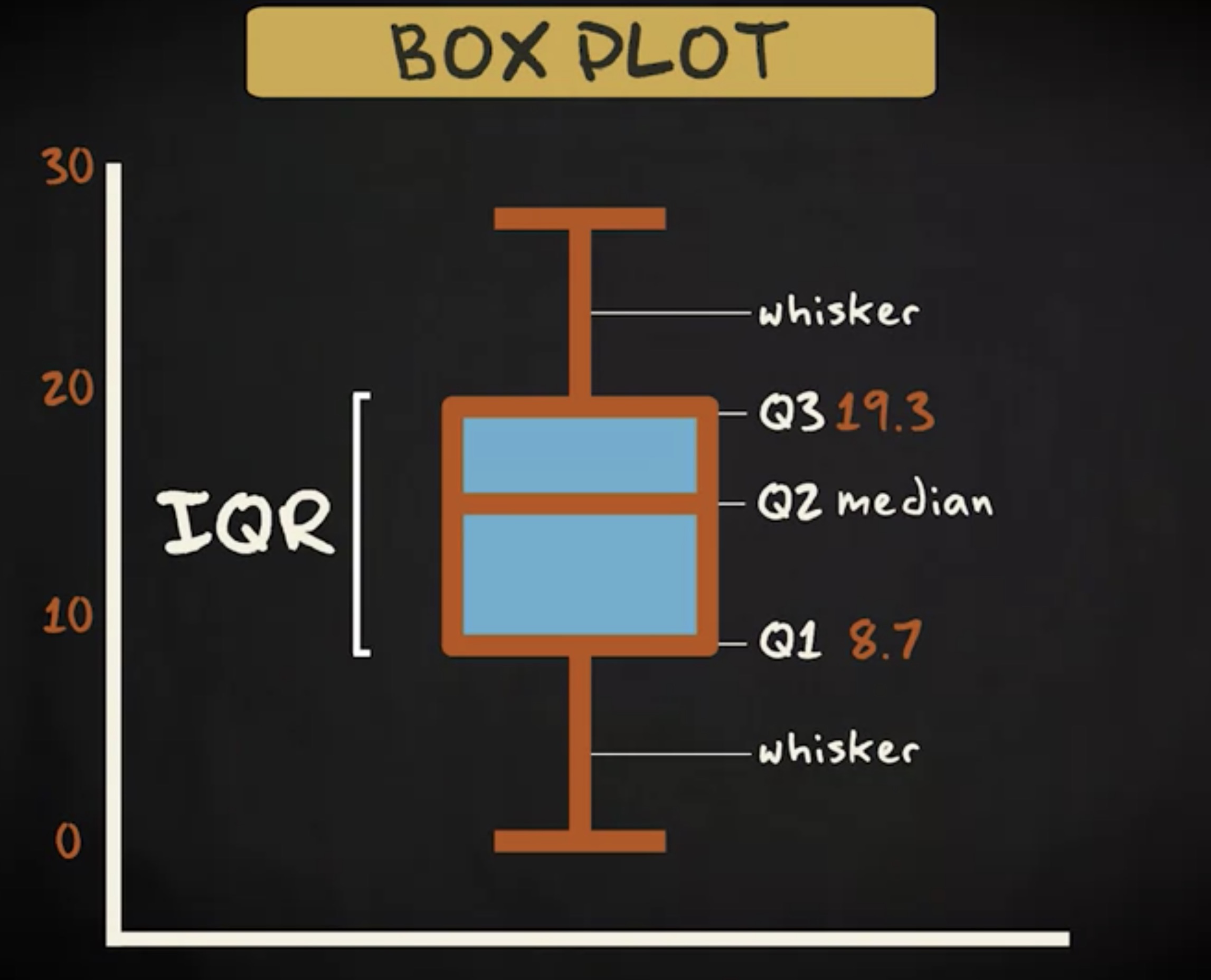
这是基于前一个示例的箱形图。箱体 本身代表分布中心的 50% 。换句话说,从 Q1 到 Q3 。 箱高 代表四分位距,箱内的 水平线 是中位数,换句话说,即 Q2 。箱体上面和下面的线称为 箱须 。它们包含除异常值以外的其他值,异常值用点单独标记。这里没有点,所以这个箱形图没有任何异常值。
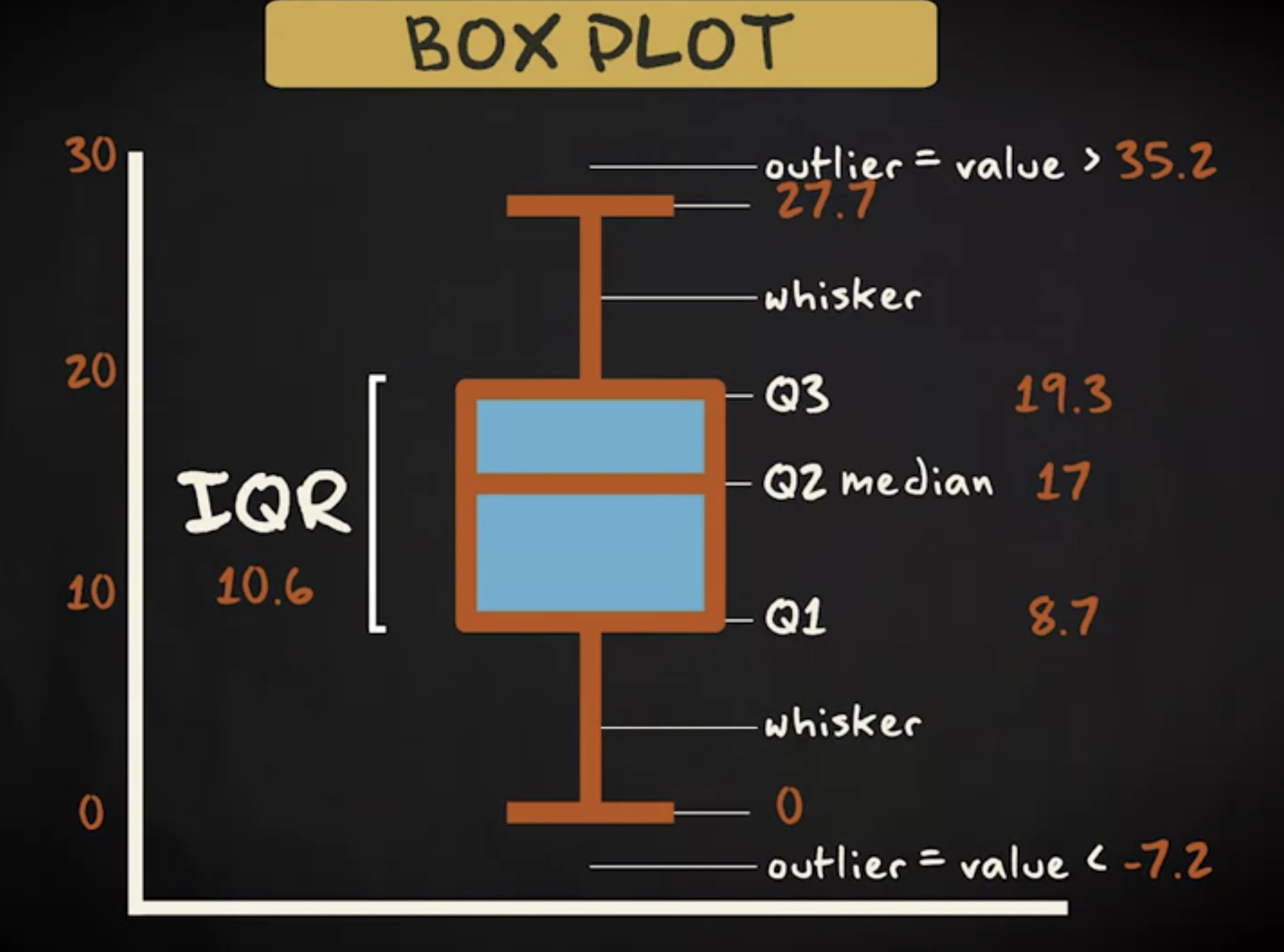
如何确定箱须的长度呢?让我们回到之前示例中的数值,我们检测到了 Q2 , Q1 和 Q3 以及四分位距。我们知道低于 Q1 1.5 倍四分位距的或高于 Q3 1.5 倍四分位距的值是异常值。这里的四分位距是 10.6 。所以 1.5 乘以 10.6 等于 15.9 , Q1 为 8.7 ,因此所有低于 8.7 减去 15.9 等于 -7.2 的值都是异常值。这里不存在这样的值,所以下末端没有异常值,这里的最小值是 0 。 Q3 是 19.3 ,因此,高于 19.3 加上 15.9 等于 35.2 的值都是异常值。我们也没有这么高的数值,所以上末端也没有异常值。箱须的上末端等于最大值,即 27.7 。
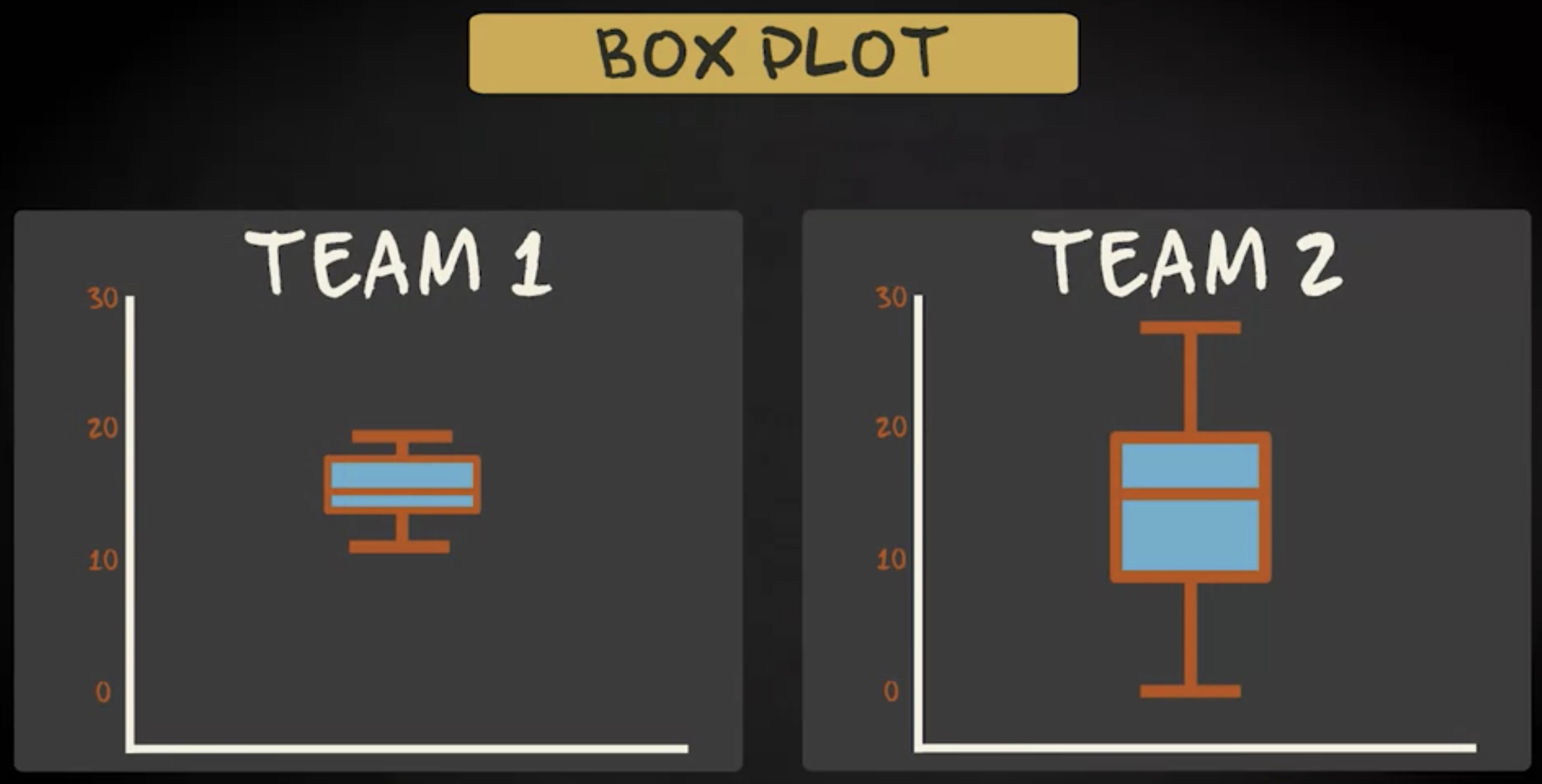
我们来看一下第一队的箱形图,如果比较两个箱形图,我们立即就能看到两个分布的变异性差别很大。
小结
请记住,分布的中心只能告诉你部分信息。为了了解的更完整,还要 评估分布的变异性。箱线图使用三个四分位数,异常值以及剔除异常值后的数据范围,以紧凑的方式显示分布的重要信息。
方差和标准差
在足球运动员中,纹身越来越受欢迎。试想,你想知道球员纹身的身体占比。

这里看到的点图表示纹身占比的分布,由两队球员纹身占身体的百分比表示。一目了然,在第一队中纹身占比的变化远小于第二队。这种变异性可以通过 全距离 或 四分位距 来测量。也可以用箱线图表示 在此可以看到相关的箱线图。在本节中,将讨论统计研究中经常使用的另外两种变异性度量,即 方差 和 标准差 。
与许多其他变异性度量相比,方差和标准差的巨大优势在于:它们考虑了所有变量的数值 。
让我们从方差开始。这是方差的公式:
s 的平方代表方差。将每次的观测值 x 减去 x 的平均值 (x 拔),然后将所有这些值平方后相加,结果是我们所说的平方和,接下来将平方和除以样本的大小 n 减去 1 。我们现在将公式应用于纹身占比的示例,以了解它在实践中的工作原理。
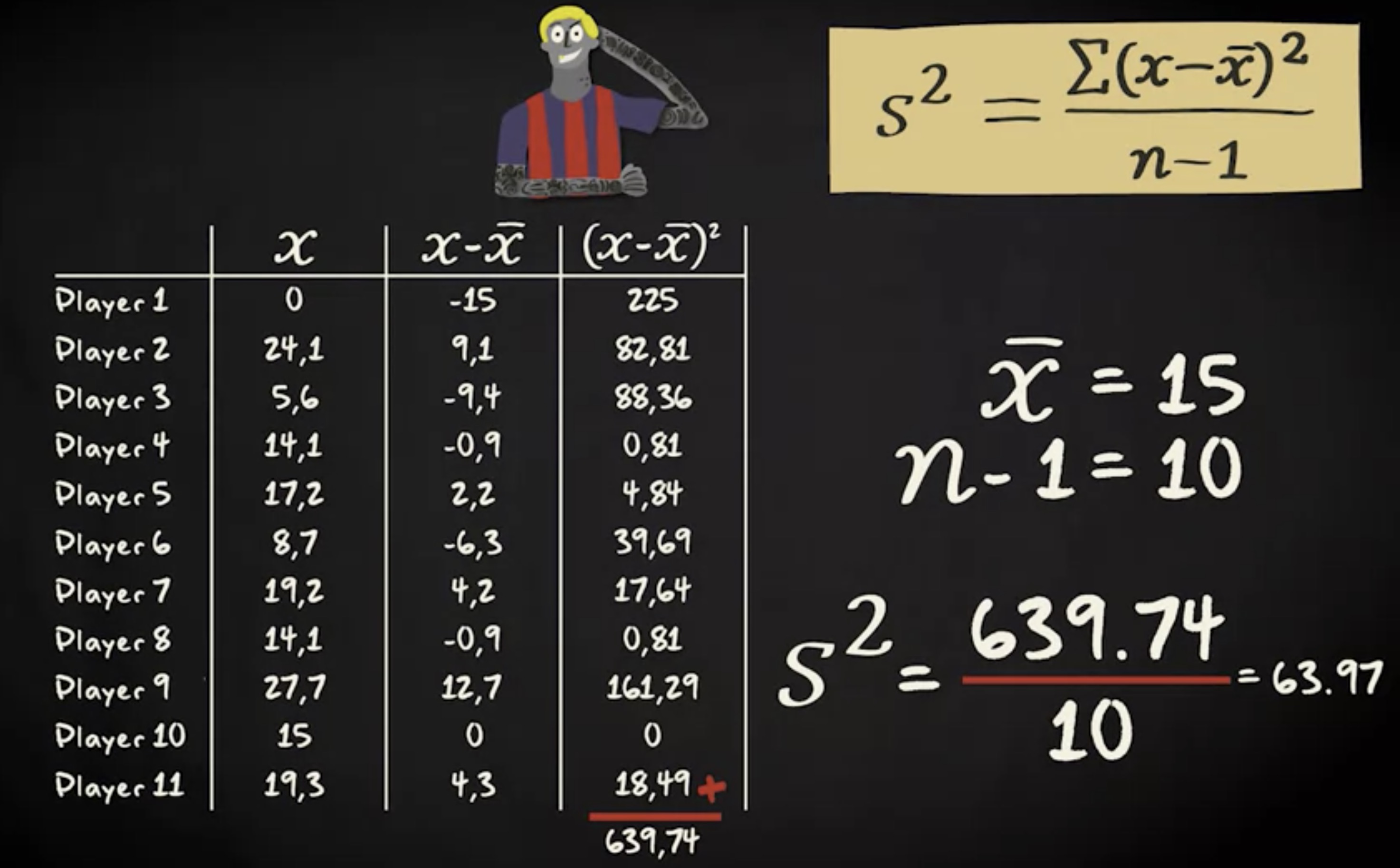
第一步是计算平均值,这些值的平均值等于 15 ; 第二步是从每个观测值中减去平均值。我们来取第一个值,0 从这个值中减去平均值 0 减去 15 是负 15 。我们对样本中所有的值都这样计算。算完后,我们发现有负数,也有正数。这并不奇怪,因为均值是这些数值的中间点或平衡点。事实上,均值的负差和正差相抵 ,结果的总和等于 0 。换句话说,这些值的总和等于 0 。
因此,我们不使用 原始差值,而是使用 差的平方 。
接下来,我们对所有这些计算值进行平方。
根据公式,接下来我们需要将所有这些值相加。现在得数是平方差的总和,换句话说,平方和。这个数等于 639.74 。然后将平方和除以 n 减 1 。在我们的例子中, n 是 11 ,所以 n 减去 1 等于 10 。 639.74 除以 10 等于 63.97 ,这就是方差。
方差越大,变异性越大。这意味着方差越大,数值越离散。
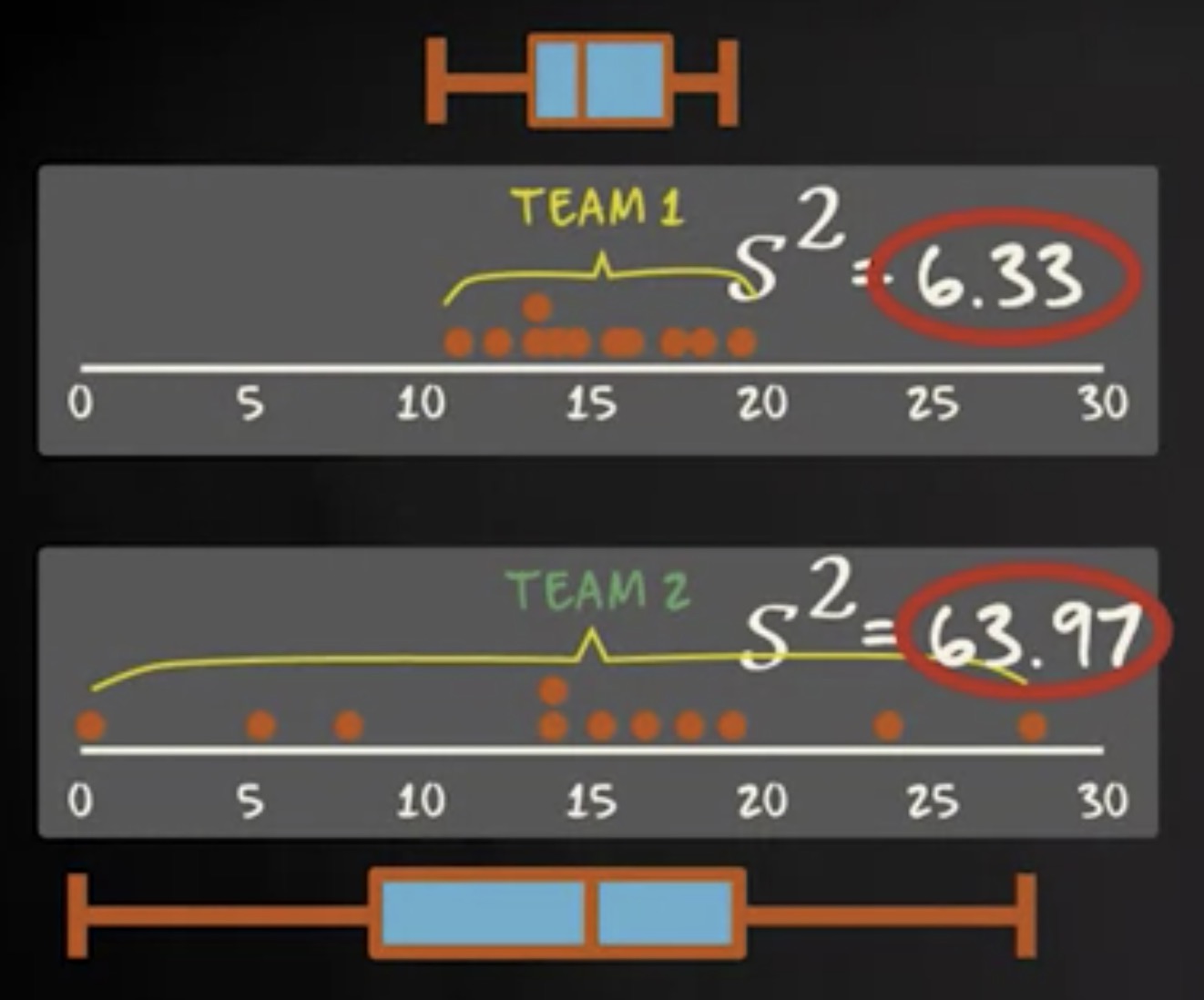
这里显示的第一队的方差约为 6.33 ,从点图和箱线图中已经可:第 2 队中纹身占比的较大差异,也由较大的方差表示。
方差的一个重要缺点是:方差的度量是经过平方的变量度量。毕竟,我们平方了正差和负差,以便它们不会相互抵消。
有一个非常简单的方案可以解决这个问题。我们只取方差的平方根 —— 我们称之为 标准差 。标准差可以被看作观测值与平均值的平均距离。标准差越大,数据的变异性越大。
因此在我们的例子中,第一队的标准差是 6.33 的平方根,等于 2.52 。第二队的标准差是 63.97 的平方根,等于 8.0 。标准差是最常使用的离散度量。然而,在许多统计方法中,方差也起着重要作用。在本节教程中,大家了解了它们密不可分,可以轻松从一个推演出另一个。

