欢迎关注微信公众号「Swift 花园」
随机性 (randomness)
识别和理解随机性,和推断它是一样重要的技能。它们不仅在统计分析中有用,对于每天发生在我们身边的日常事物,同样有意义。这篇教程中,我将向你解释为什么人们如此不擅长应对随机性。
想象你在海滩上看着海浪翻滚,然后你注意到一枚美丽的贝壳,它的个头和形状明显地异于周围其它贝壳。于是你想想看附近还有有没有这种贝壳。这是一项无法预见的行动计划 —— 贝壳可能是随机分布在这个巨大的海滩上的。因此,你找到另外一枚同类贝壳的时间是不确定的,甚至你都可能找不到一枚相似的。
你开始思考这件事,然后你意识到随机性几乎在日常生活中无处不在。所以,无怪乎我们有丰富的词汇来描述它,比如不确定性、机会、风险、可能性。还有,变异性和不确定性的程度能够非常精细地描述随机性。
看看下面这组词汇:罕有、少见、有时、普通、频繁、经常。有意思的是,某件事是否随机,不仅是现象自身的特性,也很大程度上取决于我们对它的认识。假如你之前就来过这片海滩,你可能已经发现过这种贝壳,从而改变这一次的搜索策略,以便增加找到更多这种贝壳的机会。你搜索的尺度也有关系,如果在很小的区域做一个短暂的搜索,可能不是很有把握找到新贝壳,但是搜索时间延长,搜索区域扩大,找到机会就会增大。
尽管有这么多的词汇,以及我们在日常经验中熟记随机性的能力,我们其实一点都不擅长量化地评估随机性。一方面,我们在真实的随机数据中寻找各种 “模式”。你一定听过一个词叫 “宿命”。另一方面,我们自身又无法制造随机熟记。有一个失败尝试的案例 —— 下图中左边的通过拼接得到的贝壳随机分布的地图,实际上是分布太规则的。而右边那幅是现实的随机分布模式,看起来有更多聚集在一起的 “簇”。

另外一个被我们用来解释随机性的例子叫 “赌徒谬误” —— 它的错误之处在于用一系列前面发生的随机现象预测未来的随机现象。人们没有意识到的是,如果你连续掷出了四次 6 ,感觉上不太可能再第五次掷出 6 。然后,这个投掷的结果为 6 的概率之前是 六分之一,之前是,现在还是。

我们之所以应对随机性孱弱,原因在于我们的大脑倾向于用记忆模式的方式衡量随机性。考量到这一点,为了量化随机性、理性思考随机性并且产出现实可行的随机模式,学习正确的方法十分重要。它们帮助我们避免错误,更准确和更有效地对我们周遭的世界做出预测。
小结
随机性并非一个现象的内在属性,它同时取决于我们对它的知识,观察方法以及我们关注它的尺度。尽管有大量表达随机性的词汇,人类天生不擅长量化评估它。我们困于宿命论,困于对某些纯随机模式的过度解读,这些操作同时也不利于构建随机性。
概率 (probability)
坚持不懈,终有所成。
尽管已经有很多关于这个概念的箴言和引证,我想再加一句 —— “毅力战胜一切”。这一节中,我将一步步引导你学会用概率来量化随机性。
人类的大脑也许并不是很适合回答随机性。但幸运的是,有一个基础的机制,它的运转极大地简化了我们的生活 —— 随机性会发生变化,从事物可变、案例稀少且无法预测,到事物恒定、案例庞大且可以预测。对于这个基础,我们甚至有一个数学上的证据,它就是 大数定律 。它有赖于独立性,也就是说,某个随机现象的结果,不受之前结果的影响。
让我举个例子,说明大数定律在现实生活中是长什么样子。还是想象你在海滩,决定搜寻贝壳。很快,你发现了海滩一共有四种类型的贝壳,随机分布,数量相等,就像下图这样:
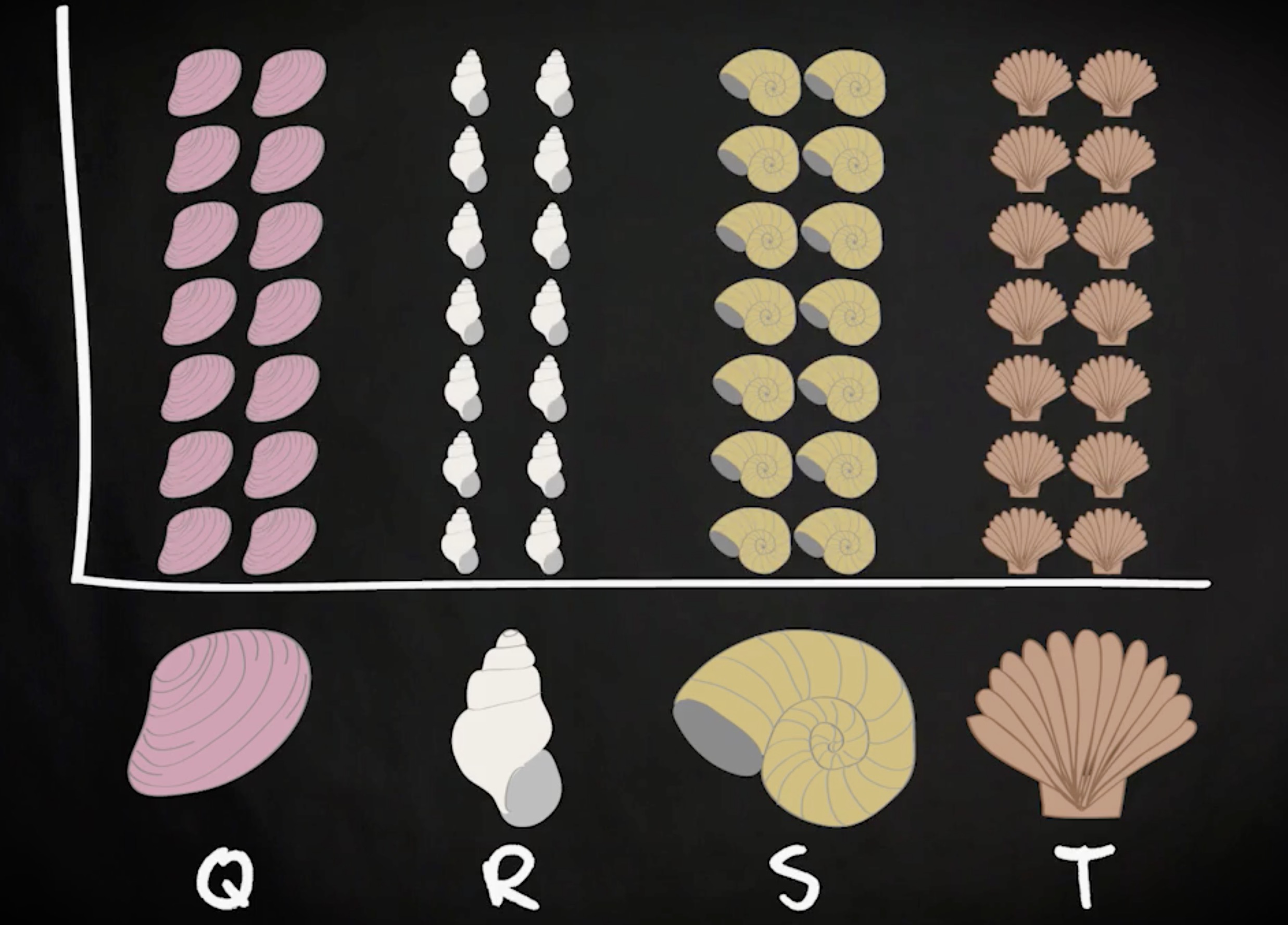
现在,你需要数出一个 Q 贝壳的分数,可以通过选取操作来完成。比如,随机选 20 个贝壳,然后计算这 20 个样本里 Q 贝壳的数量。结果如下:
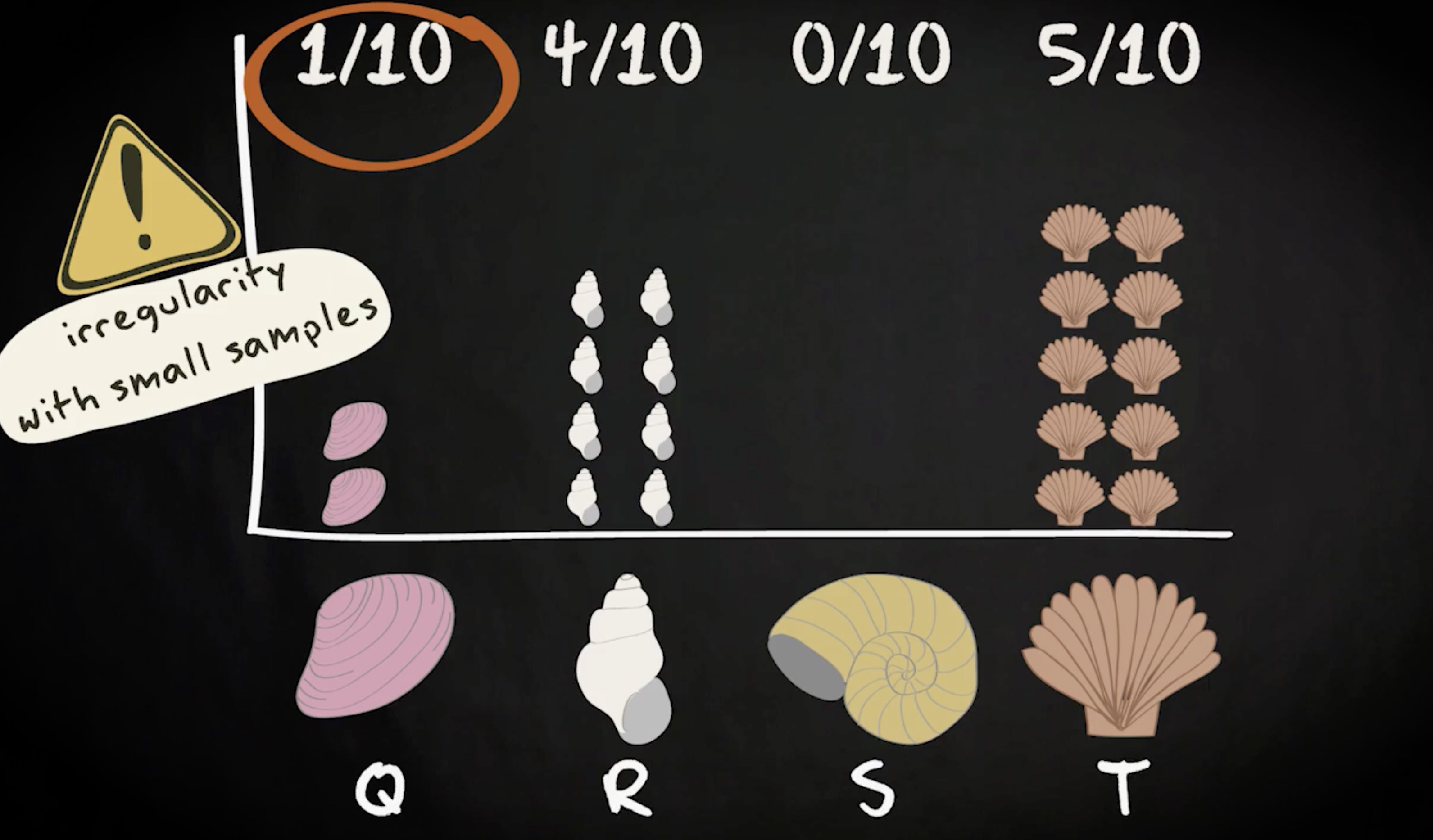
如你所见,20 个贝壳只有 2 个 Q 贝壳。 相对频率 (relative frequency) 是十分之一。基于你的推理,这个分数本来应该是在四分之一左右。 但是,你也知道,小样本的不规则性,是随机性的本质。所以呢?“保持冷静,继续前进。”

不着急下结论,继续选取更多的贝壳,观察比例如何变化,一直演化到四分之一 —— 这种比例被称为 “累积比例 (cumulative proportion)” 。

每一次你随机选取新的贝壳时,都被看作是一次可能带来 Q、R、S、T 四种贝壳之一的机会实现。用概率的术语来说,操作的结果,也就是你拿到的贝壳的类型,被称为 事件 (event) 。选取贝壳的这个行为被称为 独立试验 (independent trial) 。整个做这么多试验的事情被称为 实验 (experiment) 。在计算相对频率的时候,因为你用贝壳总数除每一种类型的贝壳,有两个属性将始终满足:每一个类型的概率将大于等于 0 或者小于等于 1 ;所有随机现象的结果的概率总和将等于 1 。

不过,现在让我们回到现实。生活并不是海滩,当然也不会有随机分布的贝壳。在日常生活中,纯粹的独立试验并不常见。通常,在随机事件之间存在 相互依赖 (interdependent) 。尽管如此,通过简化的假定,概率经常还是可以被很好地量化。此外,你需要拿到充足数量的样本,以便大数定律能发挥作用,确保你要估计的概率接近它的实际值。
小结
- 概率是一种量化随机性的方法,它可以用相对频率的均值来表示。根据这个定义,概率会始终大于等于 0 ,并 IE 小于等于 1 。所有可能事件的概率总和等于 1 。
- 正式的定义用到了实验、事件和独立试验的概念。某个事件的概率是通过它出现在整个实验中的相对频率来计算的。实验包含一系列独立试验。举个例子,掷骰子是一个事件,而每次掷出是一个独立试验。
- 让大数定律发挥作用的好方法是保持冷静,持续试验,直到 累积概率 (cumulative probability) 不怎么变化为止。

