欢迎关注微信公众号「Swift 花园」
回归 —— 找到 “那根线”!
最近的一项研究表明,吃大量的巧克力可能是个好主意。
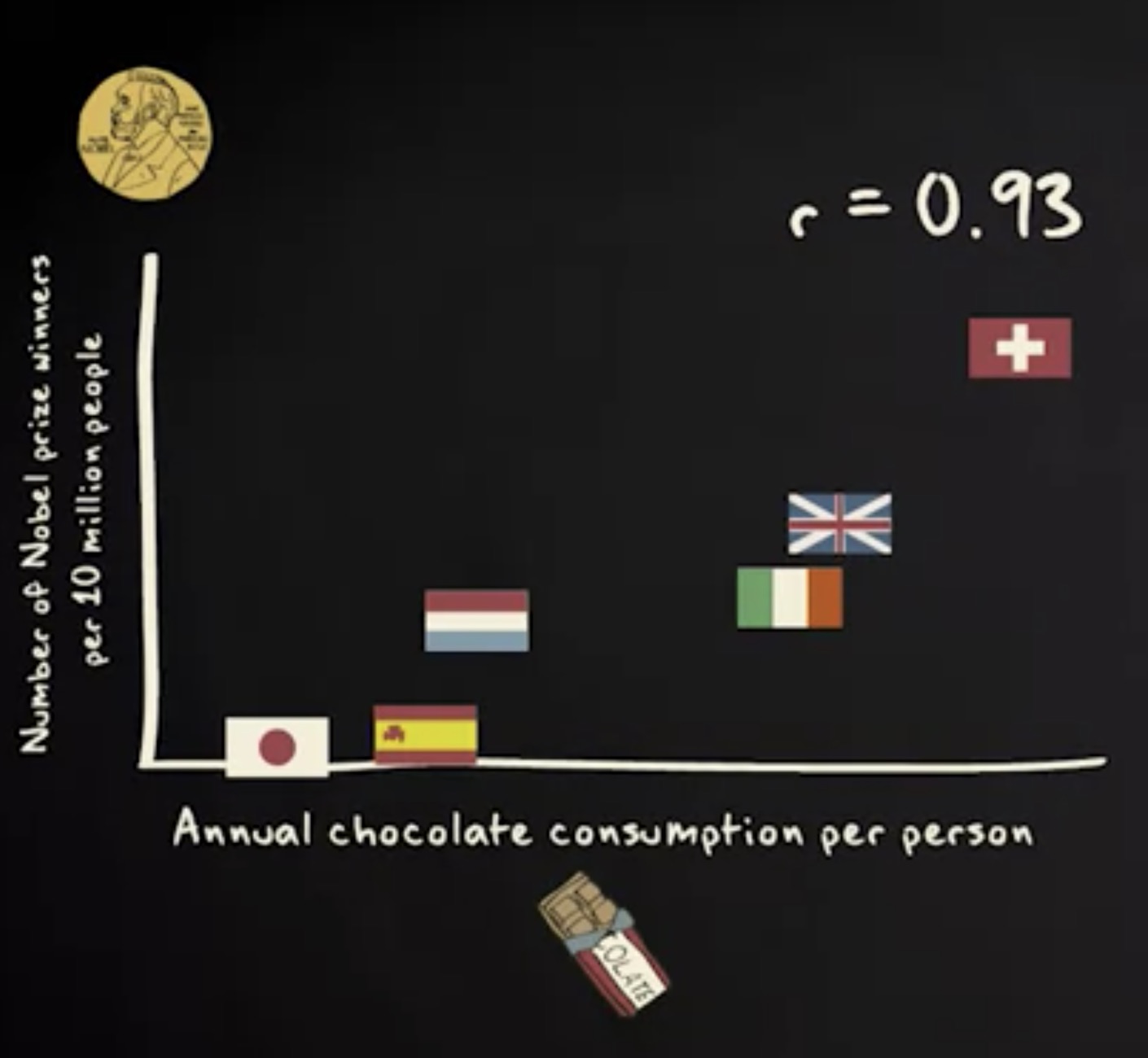
这个散点图展示了一个国家每个人年均消费的巧克力数量。可以看出,一年中人们吃的巧克力数量,跟这个国家每百万人口中的诺贝尔奖获得者人数,呈正相关性。
注意,这个散点图里的巧克力消耗量显示为自变量,而诺贝尔奖获得者人数显示为因变量。
散点图里分析的单位是国家。如你所见,相关性很高。实际上,这里的皮尔逊相关系数是 0.93 。这说明,多吃巧克力虽然可能令你发胖,但同时也让你变聪明。皮尔逊相关系数告诉我们,两个连续变量之间的线性相关性有多强,这种线性相关性被显示为一根直线。在我们的案例中,是这条线。
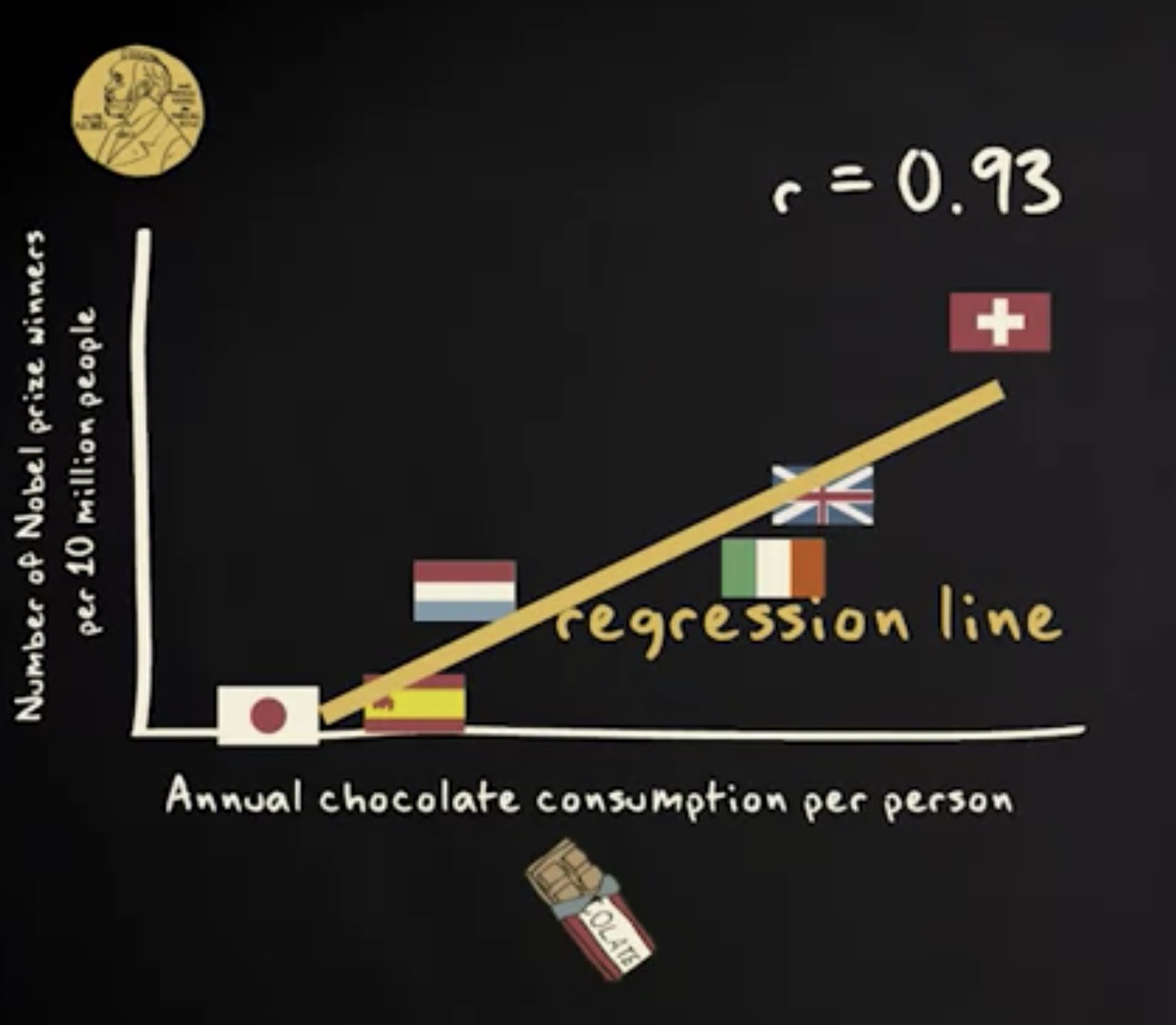
这就是我们所说的 回归线 (regression line) 。在本节教程中,我将告诉你如何找到回归线。重要的是要知道我们如何找到这条线,而不仅仅是因为回归线向你展示了两个变量之间的关系。 找到回归线是许多统计分析的基础。
那么,我们如何找到回归线呢?想象你正在绘制散点图里每一条可能的直线。所以,你像下面这样画了许多可能的线。这是一组数量巨大的线。实际上,这几乎不可能做到。不过,暂时想象你有超能力 —— 你能做到这一点。

接下来,你可以测量每条可能的线与每个案例之间的距离。在我们的例子,即线到每个国旗之间的距离。
让我给你举一个基于随机线的例子,比如,下面这个。测量日本和线的之间的垂直距离,西班牙和线之间的距离等等。直到你知道你的研究中每个案例的距离。

每一个距离都被称为 残差 (residual),你最终会得到正的残差,它们以线之上的案例到线之间的蓝色线段展示;以及负的残差,它们以线之下的案例到线之间的红色线段展示。
你为每一条可能的线测量残差。最终,我们选择一条能够 使得残差的平方和最小的线 ,这便是我们要找的那根线。

为什么是残差的平方和呢?因为正的残差和负的残差会相互抵消。
最佳拟合的线被称为 回归线 ,分析的方法被称为 普通最小二乘回归 (ordinary least squares regression) ,这是指我们找到这条线的方式。
在实践中,几乎不可能绘制每一条可能的线和残差的和。幸运的是,数学家已经找到了寻找回归线的技巧。我不会解释这个把戏在这里是如何运作的,因为它相当复杂。目前为止,知道它基于残差的平方和就已经足够了。
小结
你学到两件事:第一,你学会如何计算并寻找回归线;第二,你了解到,吃巧克力很可能有助于你通过这门课程。:D
回归 —— 描述 “那根线”
回归线是最好地描述两个变量之间线性关系的直线。但我们要如何描述这条线的样子呢?
这是一个非常重要的问题,因为通过用公式描述,我们可以很容易地把 回归的分析 (regression analysis) 传达给其他人,预测其他国家的诺贝尔奖获得者人数,以及确定不符合该模式的国家。基于此散点图中的回归线,我们可以预测:每年巧克力人均消费量为 6 公斤的国家,平均每 1000 万个人中有 11 位诺贝尔奖获得者。
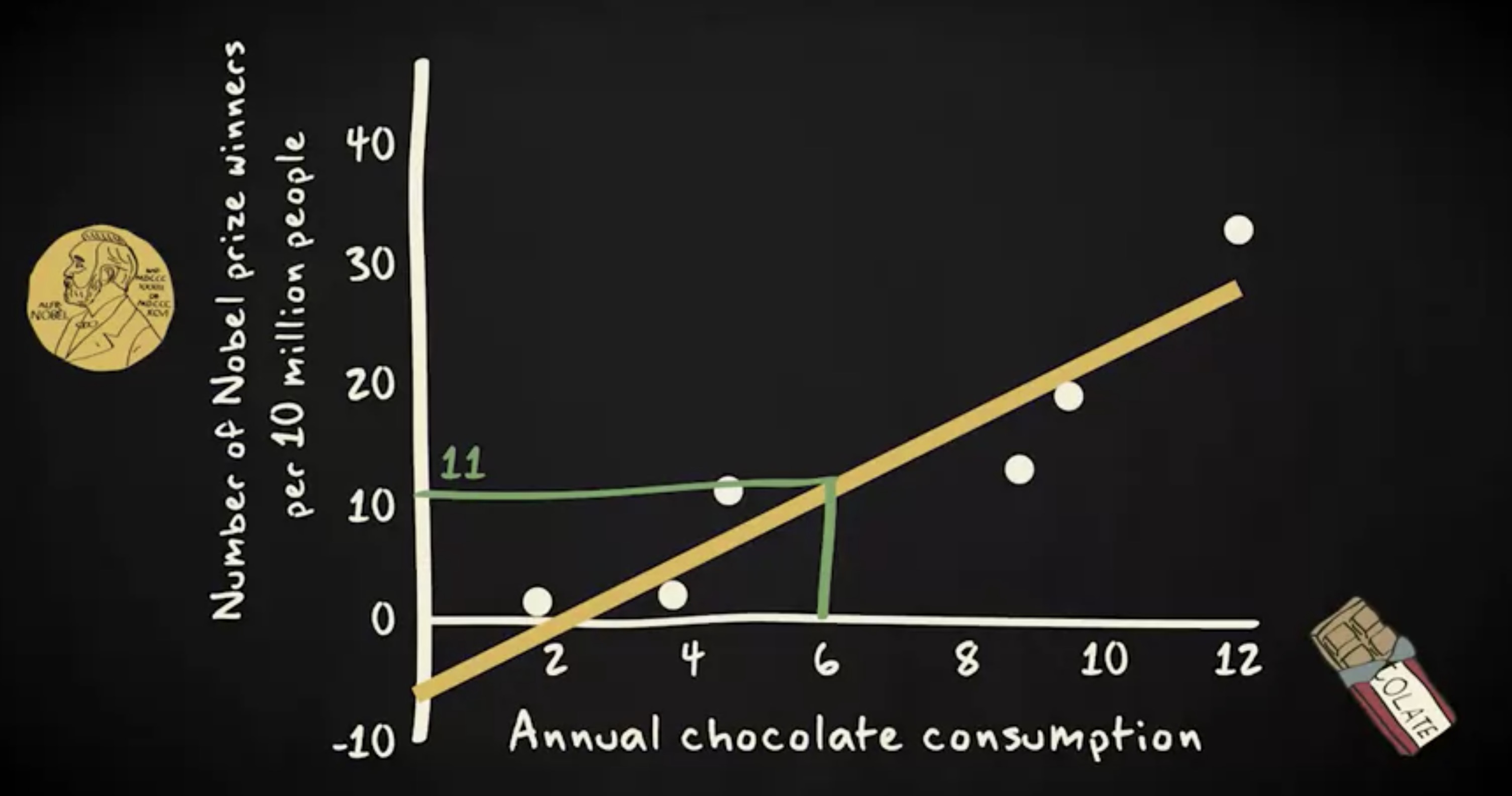
同样,基于同一条线,我们将预测一个每年人均巧克力消费量为 11 公斤的国家,平均每 1000 万人中 会有 25 个诺贝奖获得者。
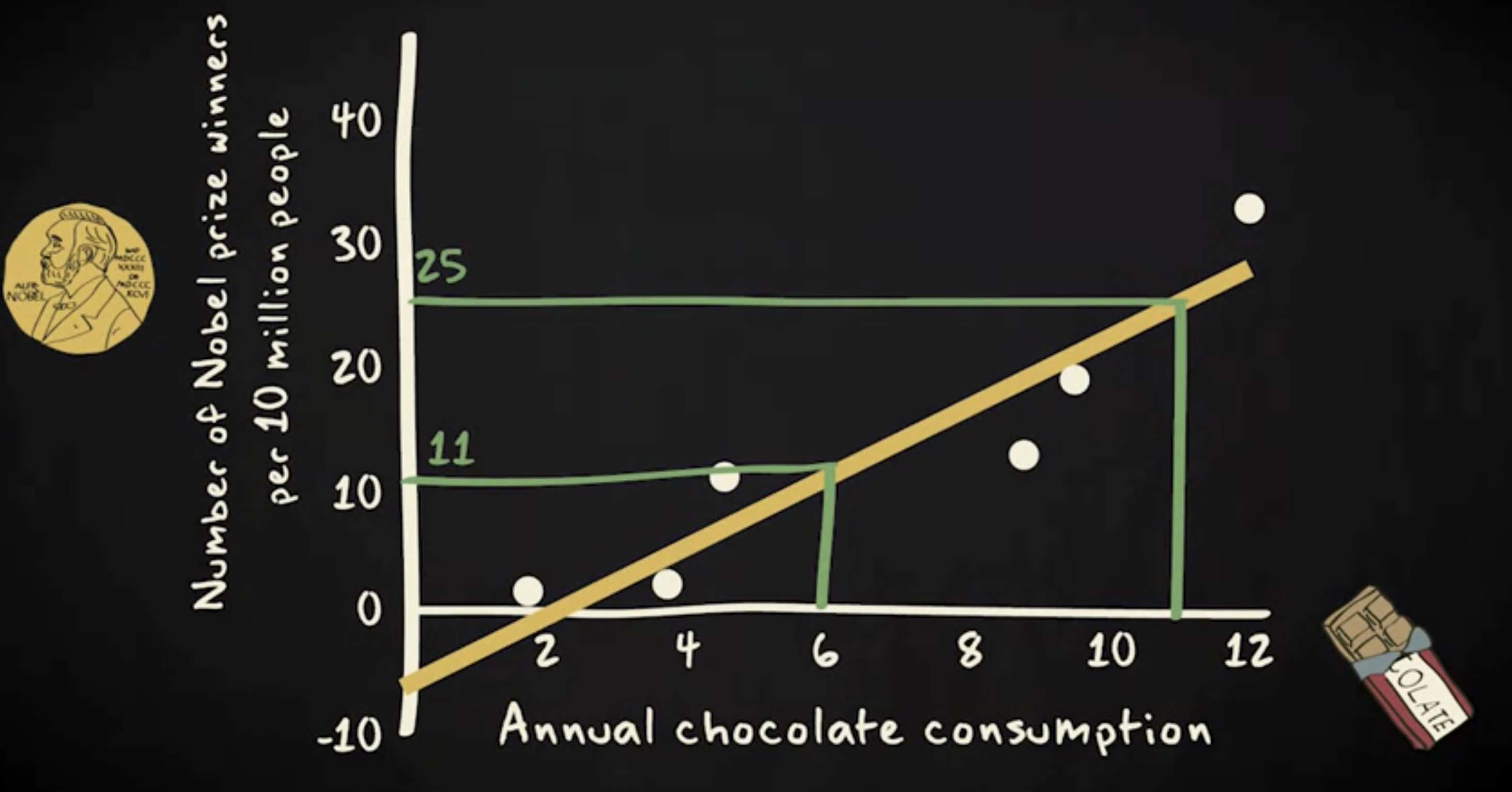
对大多数国家来说,这一预测并不完全正确。毕竟,大多数国家并不恰好在回归线上。然而,这是我们能做出的最好的预测 —— 根据我们掌握的信息。
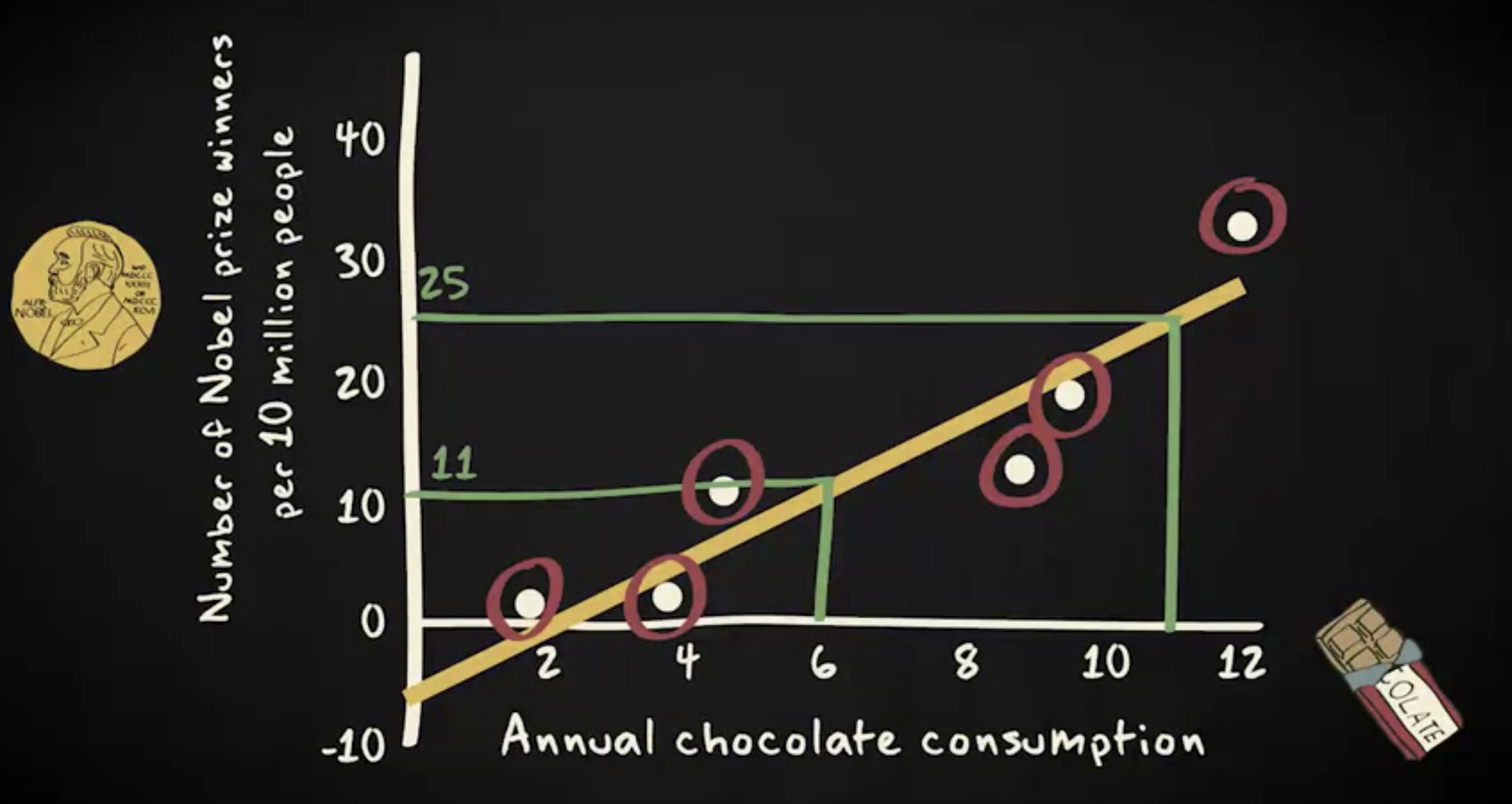
有一个简单的公式,我们可以用它来描述回归线。这就是那个公式。
$\hat y$ 不是 y 的实际值,但它表示 y 的预测值。例如,当 x 等于 12 时, $\hat y$ 等于 28 。 请注意,在这种情况下, y 的实际值为 33 。但是, y 的预测值是回归线上的 y 的值。这意味着,正好在回归线上所有的值是 $\hat y$ 。
a 就是我们所说的 截距 ,它是一个常数。当 x 等于 0 时,它是 y 的预测值。换句话说,当回归线上 y 的预测值与 y 轴的相交时, x 等于 0 。在我们的案例里,它是 -5.63 。请注意,这个值没有实质性的含义。不可能每 1000 万人中有 -5.63 名诺贝尔奖获得者。它只有一个目的:描述回归线的数学性质。
b 就是我们所说的 回归系数 (regression coefficient) 或 斜率 (regression slope) 。 它是当 x 增加一个单位时, $\hat y$ 的变化。在我们的例子中,我们看到当 x 增加一个单位,例如,从 4 到 5, y 的预测值增加 2.80 个单位。
因为是一条直线,回归线的斜率是处处相等的。所以,如果我们看看当 x 从 8 增加到 9 时会发生什么, $\hat y$ 也是增加 2.80 单位。我们案例中的回归系数为 2.80 。这可以推导出下面这个 回归方程 (regression equation)。
请看这两条回归线。它们具有相同的回归系数或 b 值。 当 x 增加一个单位时,第一条线和第二条线的 y 值增长的量是一样的。但是,这些线具有不同的截距,或一个值。毕竟,它们在不同的位置上穿过 y 轴。
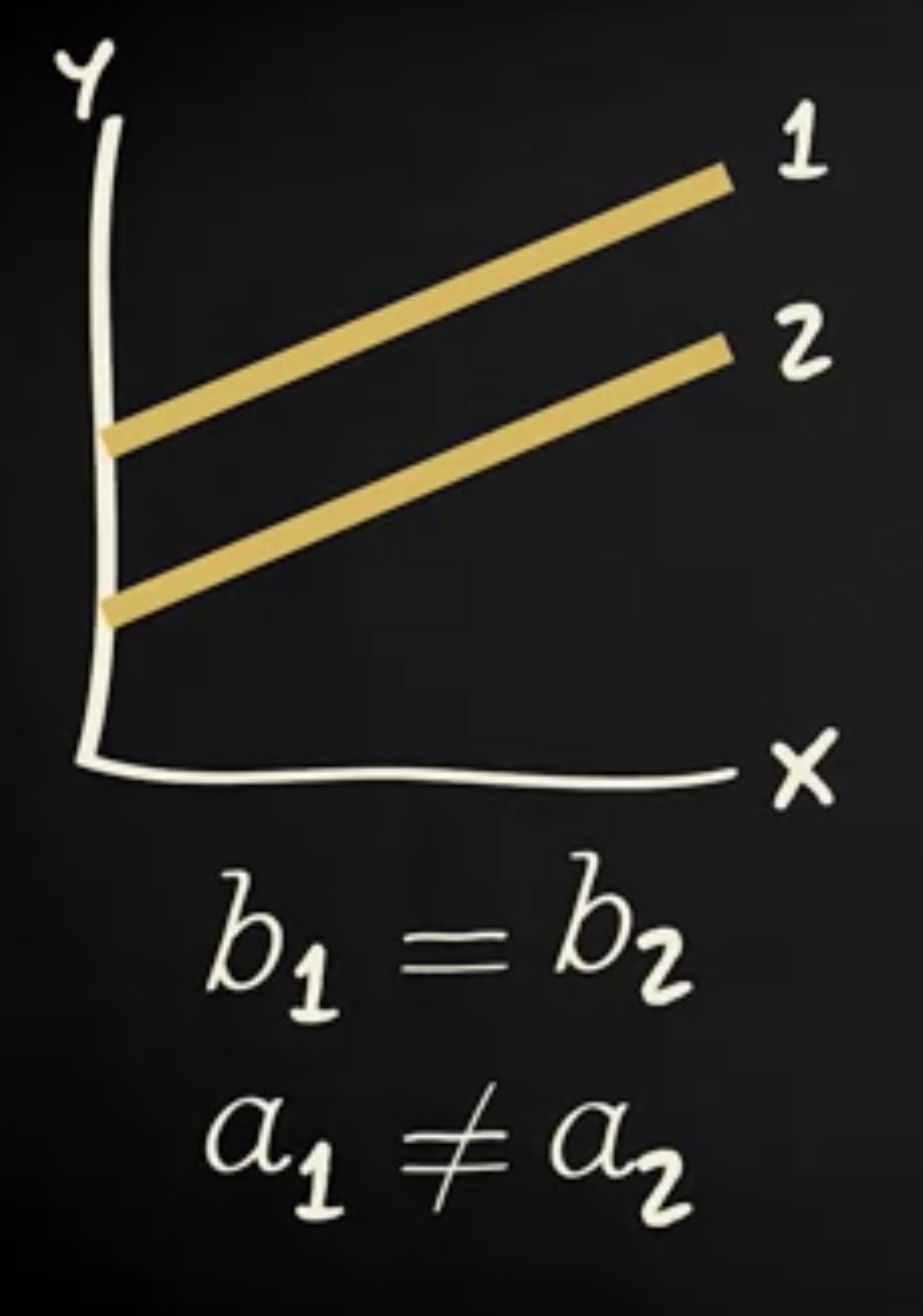
这两条回归线具有不同的回归系数。当 x 增加一个单位时,第一条线上的 $\hat y$ 比第二号线上的 $\hat y$ 增加地更多。然而,这两条线的截距是相同的,因为它们在同一个点穿过 y 轴。
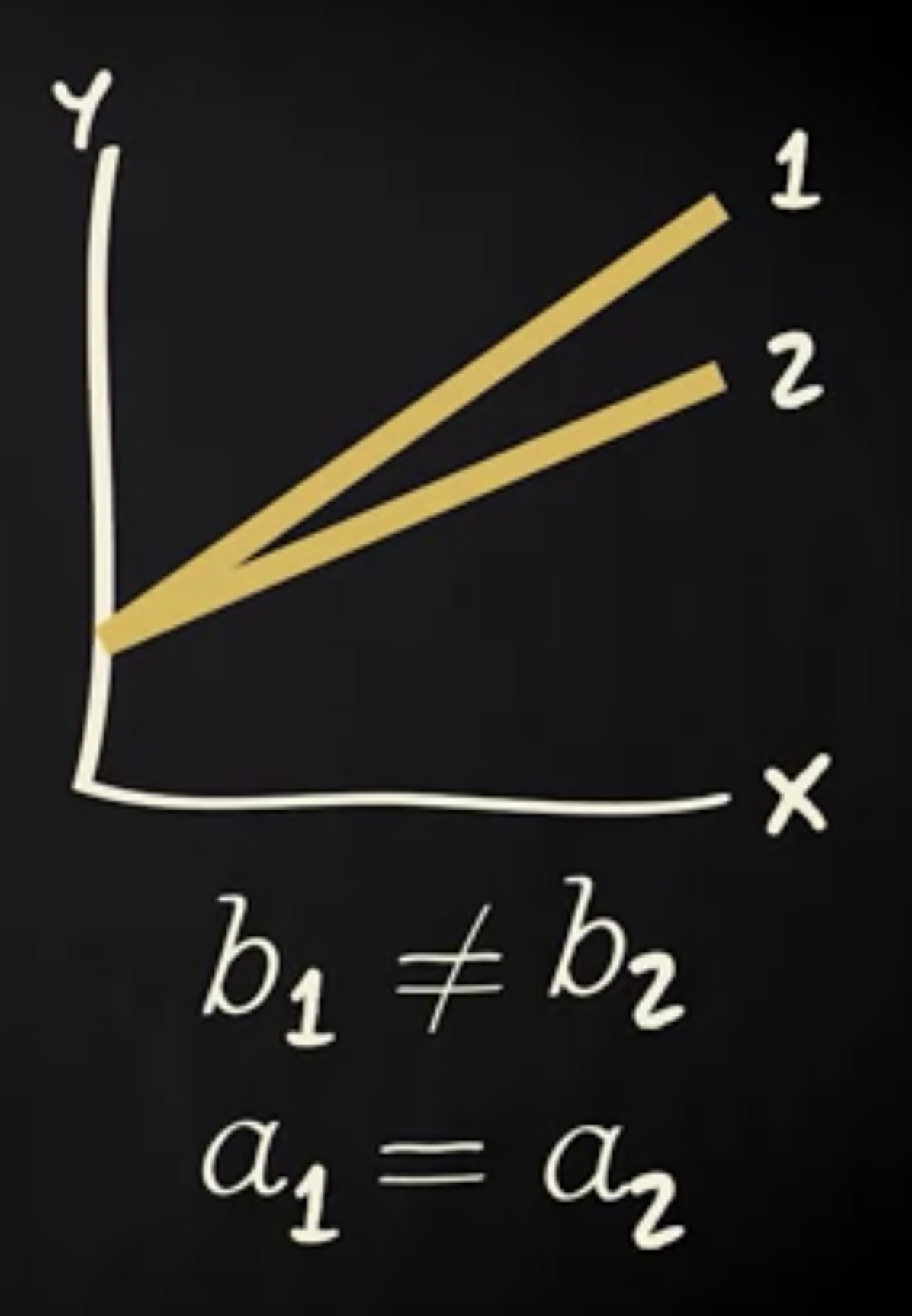
我已经对你说过了,我们可以用回归线来预测 y 值 —— 基于给定的 x 值。我们还可以使用回归公式进行预测。让我们用一个回归公式。 $\hat y = -5.63 + 2.80x$ 。我们可以使用公式预测 y 值。如果 x = 3.5,该怎么办?我们得到 -5.63 + (2.80 * 3.5)。 这就得出了 4.17 。 所以这里的 $\hat y = 4.17$ 。 如果 x = 10.21,该怎么办? 然后你得到 -5.63 + (2.80 x 10.21) 。 这使得 $\hat y$ 等于 22.96 。 当我们只看回归线时,我们得到了相同的值。对于 x 值等于 3.5 时,我们得到的预测 y 值约为 4 。 对于 x 值等于 10.21 时,我们得到的 $\hat y$ 值约为 23 。 你已经可以看到,使用公式有一个巨大的优势 —— 你可以做出更精确的预测。
通常情况下,计算机会为你找到回归线,所以你不需要自己计算。然而,当你知道你的变量的均值和标准差,以及相应的皮尔逊系数,你可以通过两个公式计算回归方程。
第一个公式通过将皮尔逊的回归系数乘以 y 的标准差,再除以 x 的标准差。这表明了回归系数事实上是皮尔逊系数的一个不标准化的版本。当 pearson 的 r 等于 0 时,回归系数等于 0 。当皮尔逊的 r 是一个正数,回归系数也是正数,当皮尔逊系数为负时,回归系数也是负的。
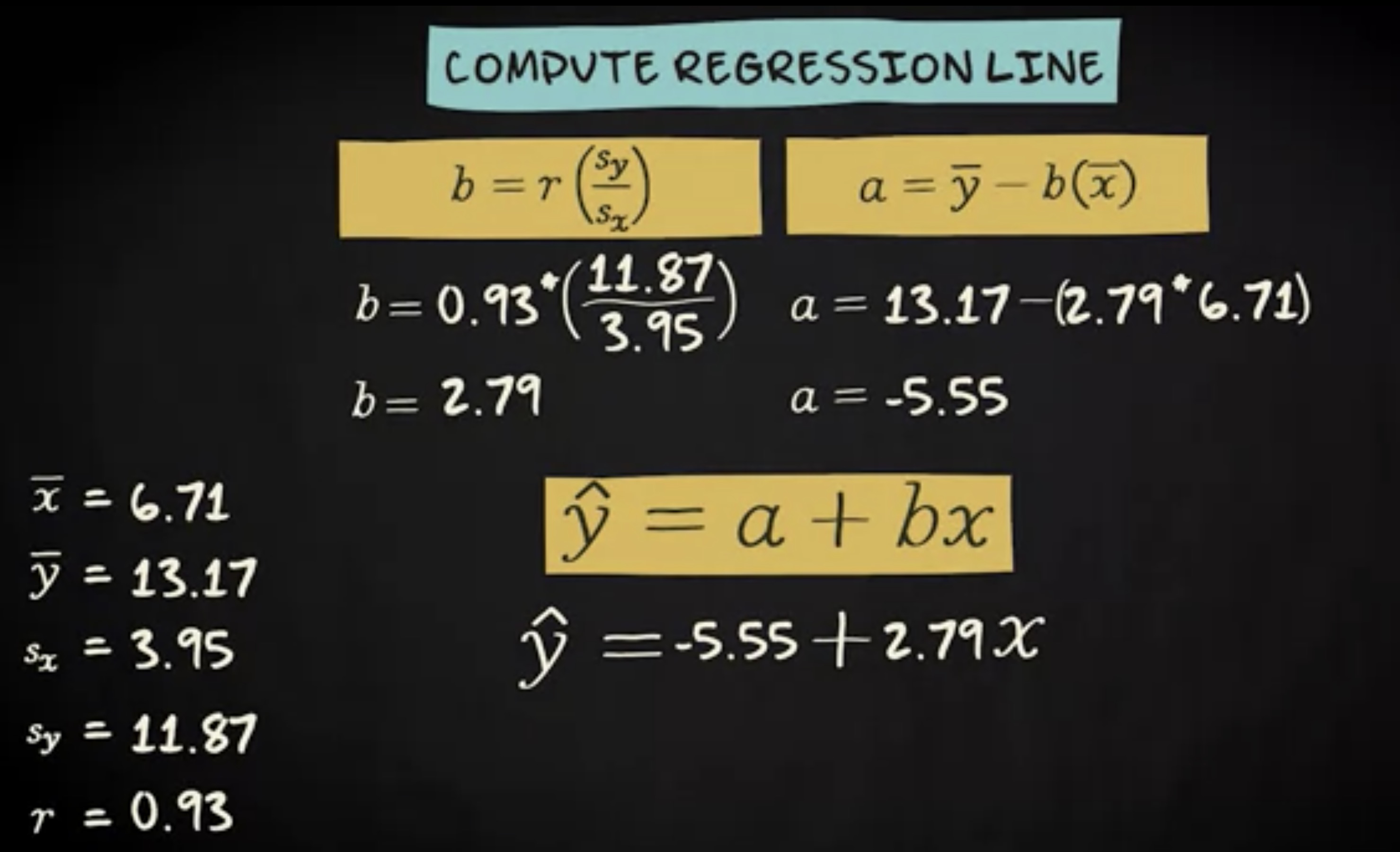
这些是我们的研究的均值、标准差和皮尔逊系数。因此,为了找到回归系数,我们乘以 0.93 * (11.87/3.95),结果是 2.79 。第二个公式用回归系数乘 x 的均值,之后从 y 的均值减去结果来计算截距。
所以 13.17-(2.79 * 6.71) 。 这样就可以得到 -5.55 了。回归方程为 -5.55 + 2.79 x 。
与这一个计算机算出的回归方程的不同是由舍入误差导致的。我用汇总均值、标准差和皮尔逊系数来计算,这导致了一个不太精确的回归方程。因此,在使用这些公式时,尽量减少舍入。恭喜你成功完成了这个教程的上半部分!现在,你可以进行回归分析并计算预测值了。了解回归的基础知识是至关重要的,因为能够了解之后的推理回归过程。
所以多看这篇教程几次。:D
如果自变量 x 是你看这篇教程的次数,并且因变量 y 是你掌握的回归分析的知识,当你这样做时,回归分析的回归斜率将是一个正数。
如果你不明白上面这句话意味着什么,立即重温这篇教程吧。
回归 —— “那根线有多适用?”
在这一节,我们来研究回归线对你的数据有多适用。
为什么需要关注回归线的适用程度呢?因为我们希望知道回归分析预测因变量的准确性有多高。回归线适用数据的程度是用一种称为 R 方 (r-squared) 的方法来表示的。
想象一下,你身处一个有 99 个其他学生的班级,你刚刚参加完一场统计学的考试。你的教授手上已经拿到随机选取的 20 个学生的考试成绩。教授想要分享这 20 个学生的考试成绩,但同时不想让大家知道这些学生是谁。因此,她匿名了这些分数的主人。

这是你看到的分数。因为是匿名的,你无从得知哪个学生拿到哪个分数。注意,最低分数是 0 ,最高分数是 10 。现在,想象你被要求预测你邻桌同学的分数。你怎么预测得到的分数会更靠谱呢?一个显而易见的答案是,用这 20 个分数的平均值,这个值时 6.8 。现在,继续想象教授还给了你这 20 个分数对应学生上一次统计学考试的分数,同样也是匿名的。结果如下:

现在,你会如何预测你邻桌的分数呢?是的,你可以利用到回归分析了。下面是回归线和 回归方程 (regression equation) 的散点图。
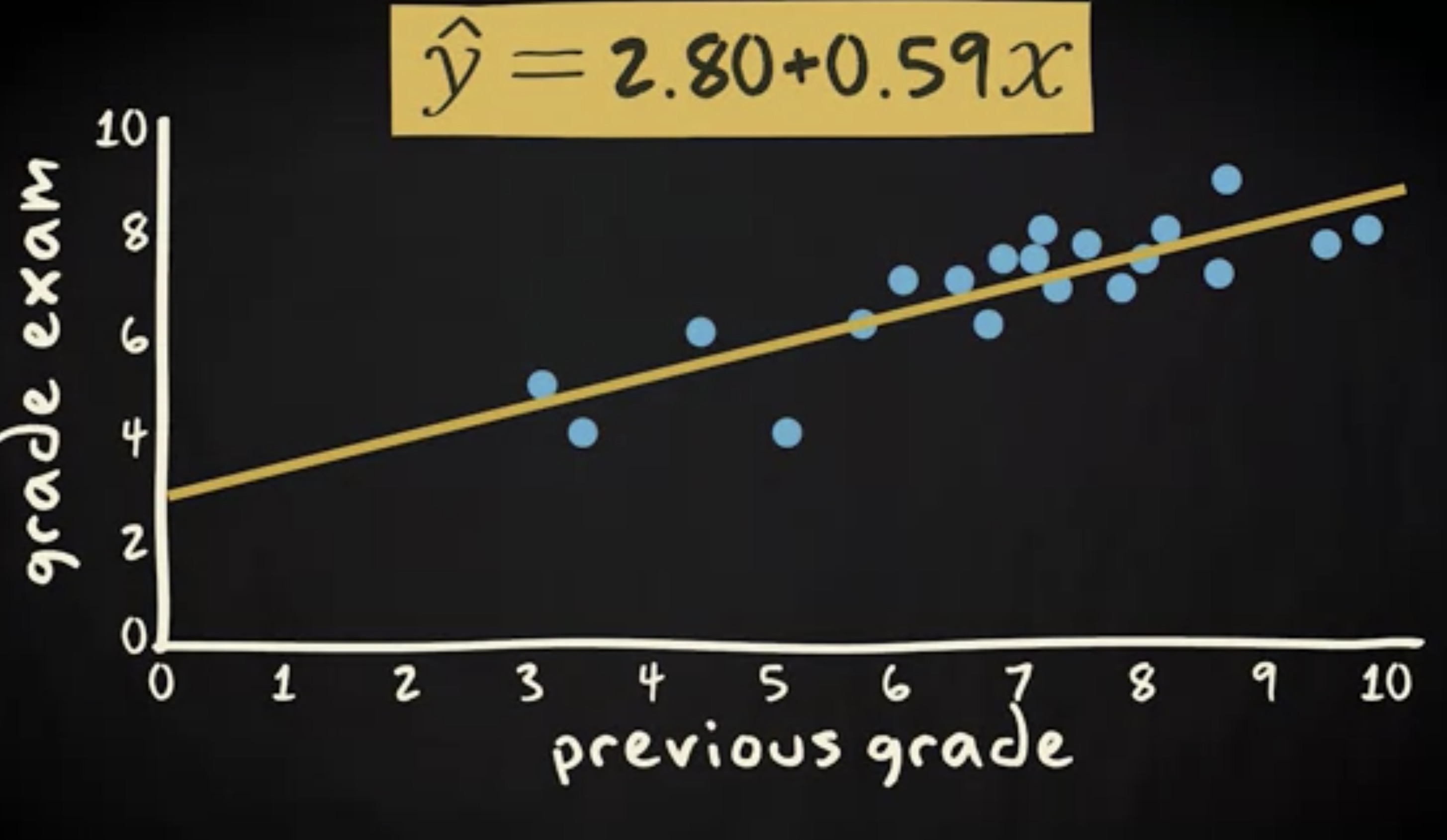
你会发现,那些在之前的考试中取得高分的同学趋向于在这一次考试中也拿到高分。实际上,你可以用这条回归线和对应的回归方程对分数做出预测。当你问到你的邻桌他之前的分数,你可以用回归线预测他这一次考试最有可能的分数。
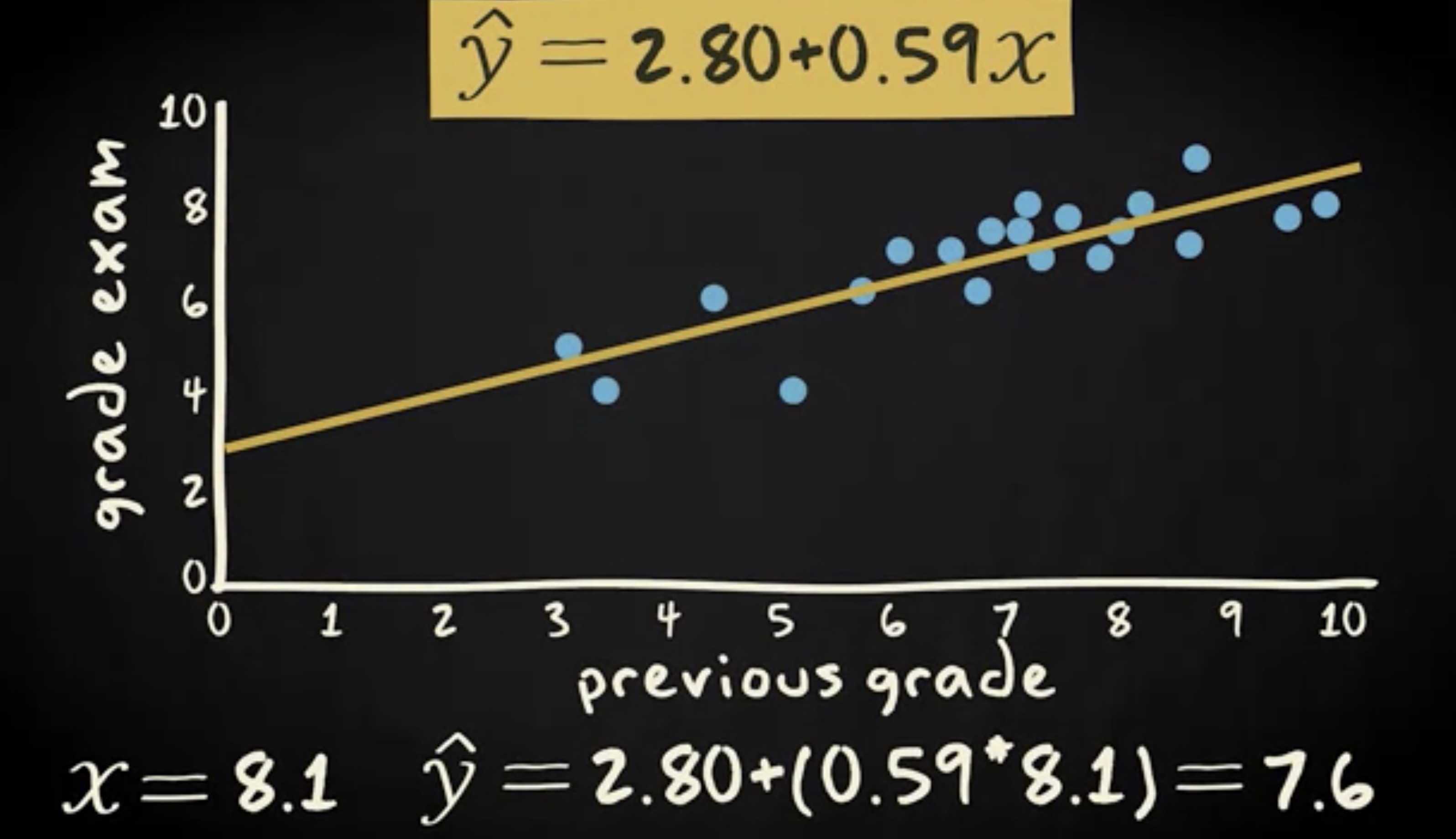
想象上一次分数是 8.1 ,代入回归方程,得到 2.80 加 (0.59 乘以 x),等于 7.6 。因此,这一次的分数最有可能是 7.6 。这是什么意思呢?当你只有一个变量的信息时,你做出的预测的准确性要远远低于你拥有两个相关变量信息的情况。R 方就是一个告诉你用回归线预测因变量而不是平均值这种方式有多适用的程度。
再回到我们的散点图。我加了一根水平线,用以表示这次考试分数的平均值。
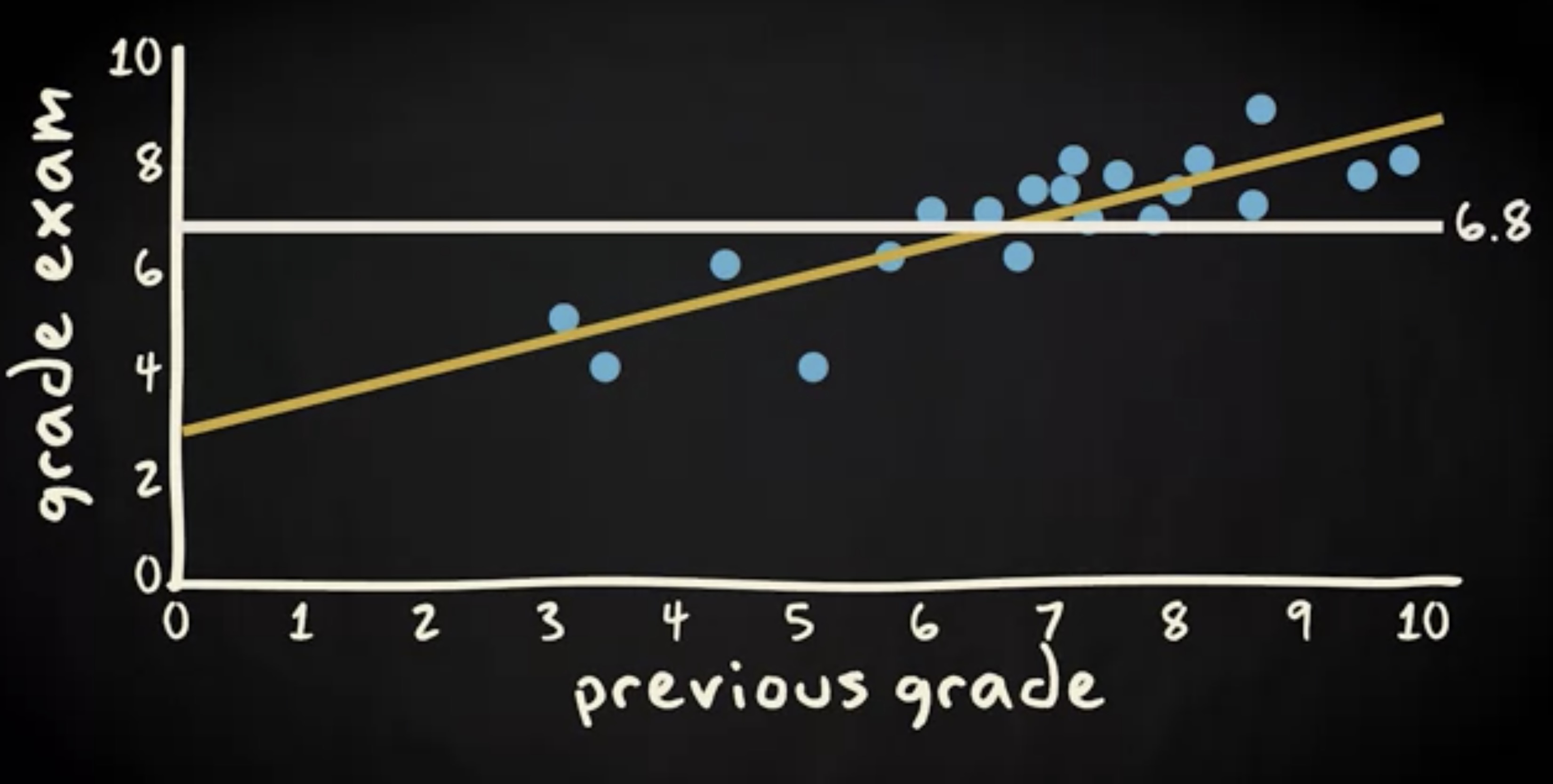
这根线之所以是水平的,是因为平均值是一个定值 6.8 ,它不会改变。可以看到,每个观察值和回归线的残差,相比于它们到平均值的残差,总体要小得多。
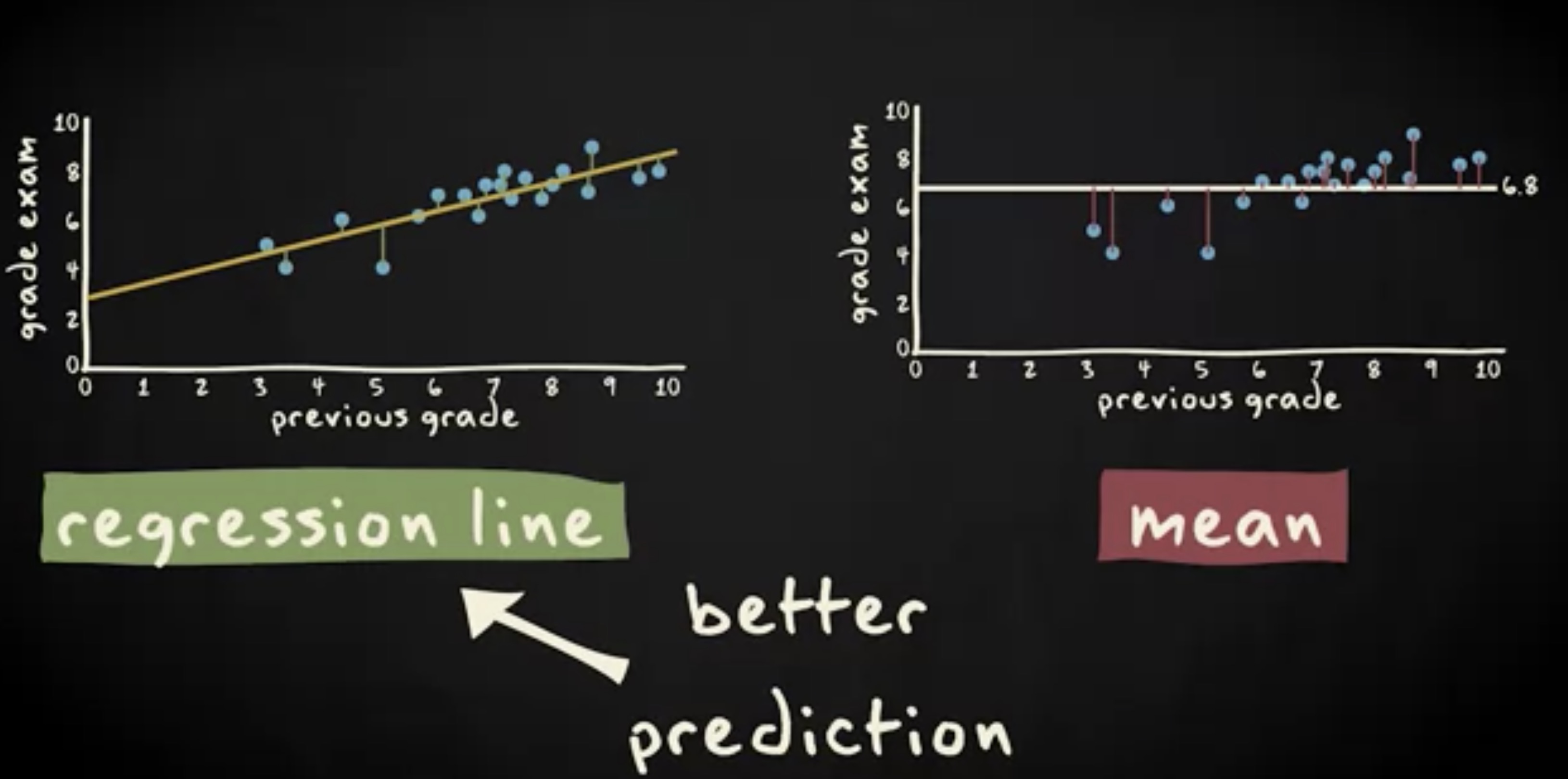
这表明,回归线的预测效果明显好于平均值。
在我们的案例中, R 方是 0.69 。这表示使用回归线预测错误的可能性比你使用平均值要小 69% 。 R 方也经常用另外一种说法来解释 —— 它是指你的因变量的方差,多大程度上可以由自变量的方差来解释。
一个变量的方差告诉你各个观察值相对于平均值的离散程度。因此,在我们的案例中,这一次考试分数的方差中的 69% ,可以被前一次考试的分数预测。用可视化的方式表达这种解释,可以用到两个圆。
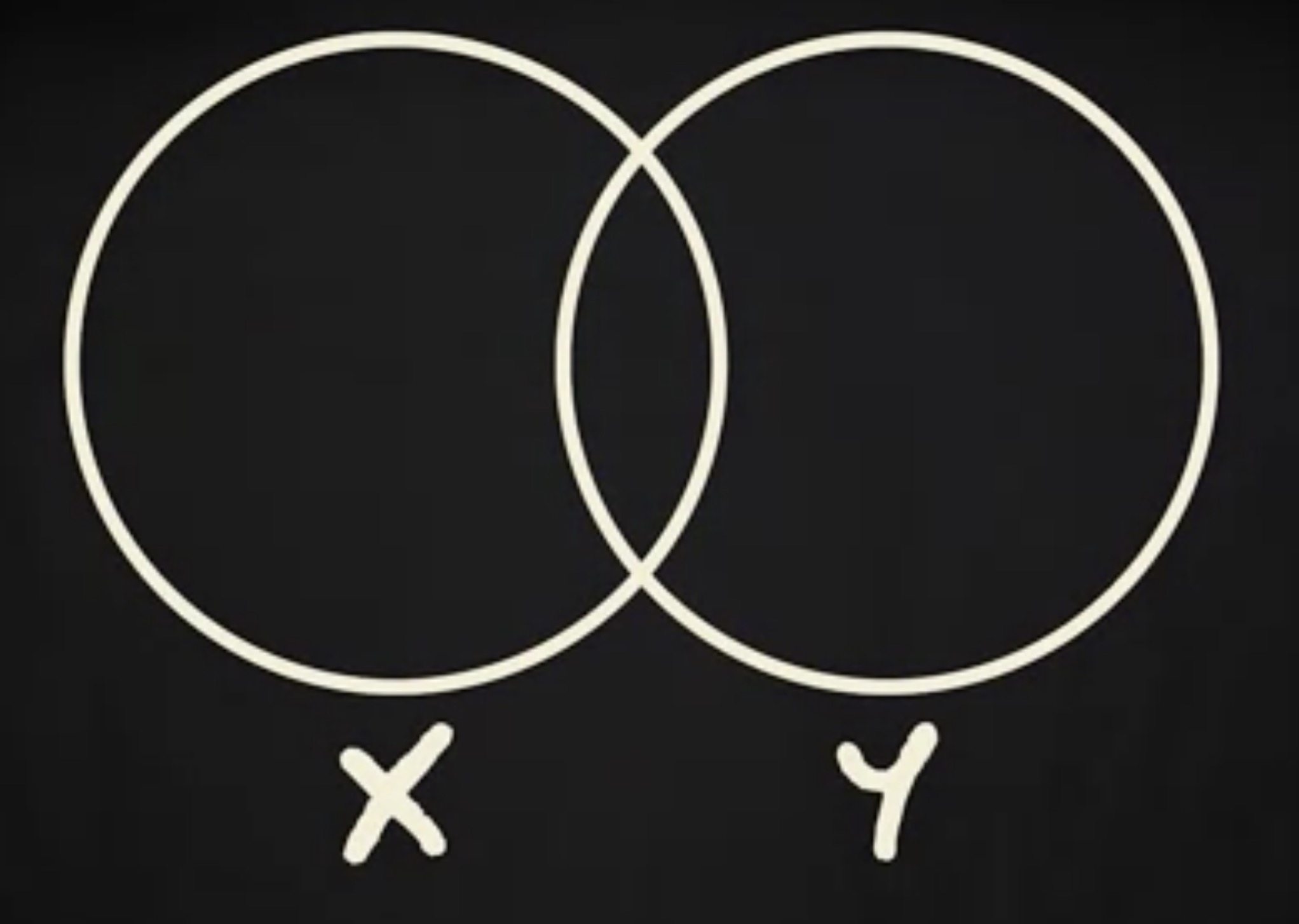
左边的圆表示自变量的方差,右边的圆表示因变量的方差。重叠的部分就是 R 方,或者说 可解释方差 (explained variance) 。当重叠部分很小时, R 方很小,重叠部分很大时, R 方很大。

你需要了解一个很重要的事实 —— R 方和皮尔逊相关系数关联紧密。实际上,正如它的名字指示的, R 方就是皮尔逊相关系数的平方。因此,要计算 R 方,只要算出皮尔逊系数然后平方就行了。
这也说明 R 方总是一个正数。在我们的案例中,皮尔逊相关系数等于 0.83 。平方得到 R 方 0.69 。注意,如果两个变量的线性相关性是完美的,那么皮尔逊相关系数和 R 方都是 1 。如果完全线性无关,那皮尔逊相关系数和 R 方都是 0 。
但是,你需要记住: R 方的含义和皮尔逊相关系数很不同。皮尔逊相关系数告诉你两个变量之间是否存在正的或者负的相关性,以及这种相关性有多强。而 R 方并没有告诉你两个变量之间关联的方向。不过,它告诉你两件事,一是回归线预测相对于平均值预测优胜多少,二是因变量的方差有多少是可以被自变量的方差解释的。

