欢迎关注微信公众号「Swift 花园」
样本和目标总体
几乎所有的统计研究都基于样本。
想象你试图知道伦敦有多少学生以嬉皮士自居,但你几乎不可能去问全部的学生这个问题。所以你决定采样,比方说 200 个调查对象,并估计有多少人把自己看做嬉皮士。
关于统计的一个好处是,它能基于仅仅这 200 个调查对象,即样本,帮助你得出关于伦敦所有学生的结论,即目标总体。这一节中,我将详细解释样本和目标总体。

如果你从目标总体约 300,000 个学生中选择 200 个调查对象作为样本,基本上你正在聚焦于总体的一个子集。如果你测量一组变量,比如性别,年龄,所在学校,等等。你可以做所有的计算,比如单一变量分析,包括众数、平均数和标准差,或者双变量分析,计算皮尔逊相关系数或者做回归分析。所有这些数字性总结都完全是基于样本,它们被称为 统计数字 (statistics) 。通常,这种总结样本数据的方法被称为 描述统计 (descriptive statistics) 。不过,在实际的研究实践中,我们经常对特定样本的总结不感兴趣 —— 我们的实际目标是对潜在的目标总体做出推断。
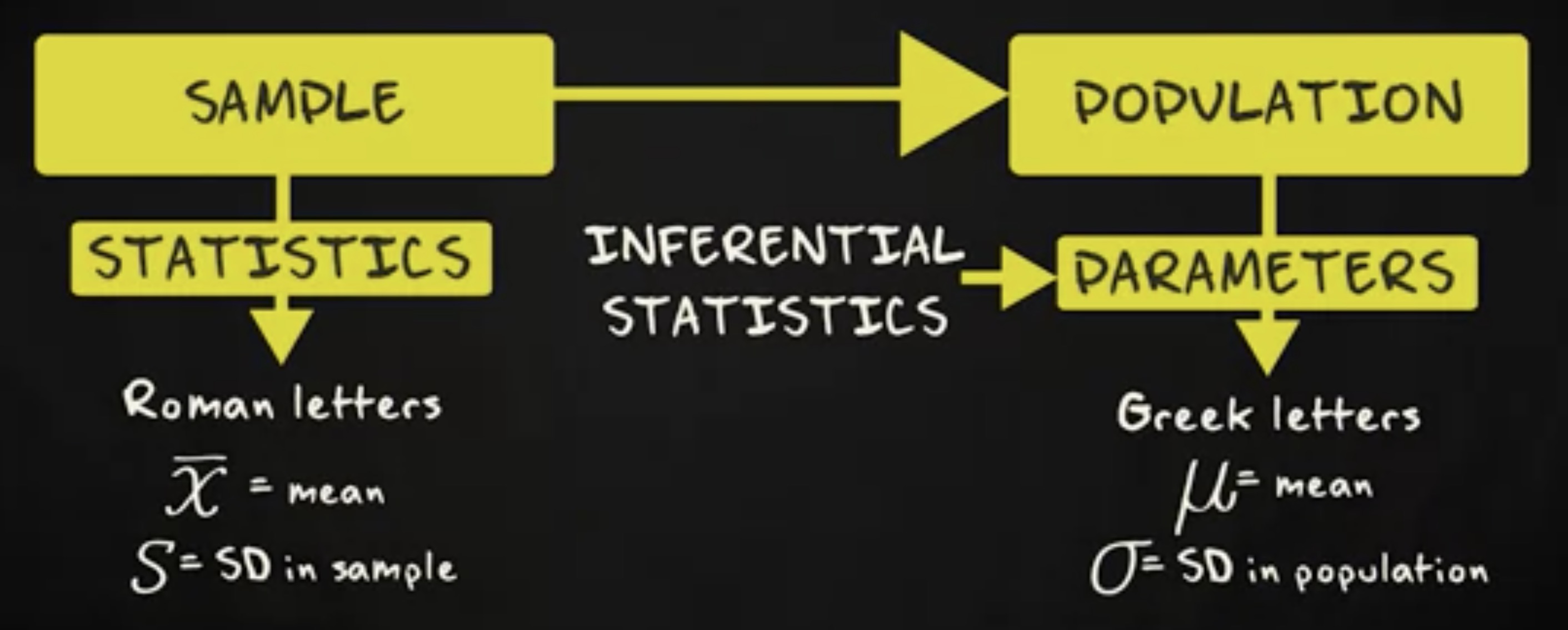
在我们的案例中,所有 300,000 个学生都在伦敦。如果我们借由样本中得到的数据推断关于总体的结论,那我们就是在使用 推断统计学 (inferential statistics) 的方法。 统计数字以罗马字母显示。例如,$ \bar x $ 代表平均数, s 是样本的标准差。 参数则以希腊字母显示, μ 代表总体的平均值, σ 代表总体的标准差。

想象你问这 200 个调查对象他们觉得自己有多大程度上把自己看做嬉皮士。他们可以从 0 到 10 表示自己嬉皮士的程度, 0 代表他 / 她根本不认为自己是嬉皮士,而 10 代表一个人完全将自己视为嬉皮士。
现在想象样本的 “嬉皮士值” 均值是 3.12 ,核心问题变成:目标总体的均值是多少?推断统计学可以帮助我们解答这类问题。
抽样
推断统计学指的是基于样本数据来得出对于总体的结论的一系列方法。可以想象,为了理解推断统计学的方法,学会如何抽取样本是至关重要的。这一节中,我将把好的抽样方法和坏的抽样方法放在一起一同讨论。同时,我会讨论到你在抽样过程中可能遭遇的各种 偏差 (bias) 。
样本是总体的子集,此外再无其他。对于推断统计学的方法来说,并非所有的样本都合用。你需要的是 代表性样本 (representative samples) 。换言之,你需要你的样本是总体的一个微型版本。为了达到这个目的,一个不错的方法是抽取 简单随机抽样 (simple random sample) 。这意味着你确信总体中的每一个对象都有相同的机会被选中。

回到嬉皮士的例子。你决定抽取 200 个调查对象。平均的嬉皮士值是 3.12 ,总体包含伦敦所有的学生,感兴趣的参数是总体的均值,样本包含 200 个被选中的学生。
你将用于推断总体均值的统计数据是样本的统计均值。为了得出结论,我们希望样本是简单随机样本。如何确保这一点呢?
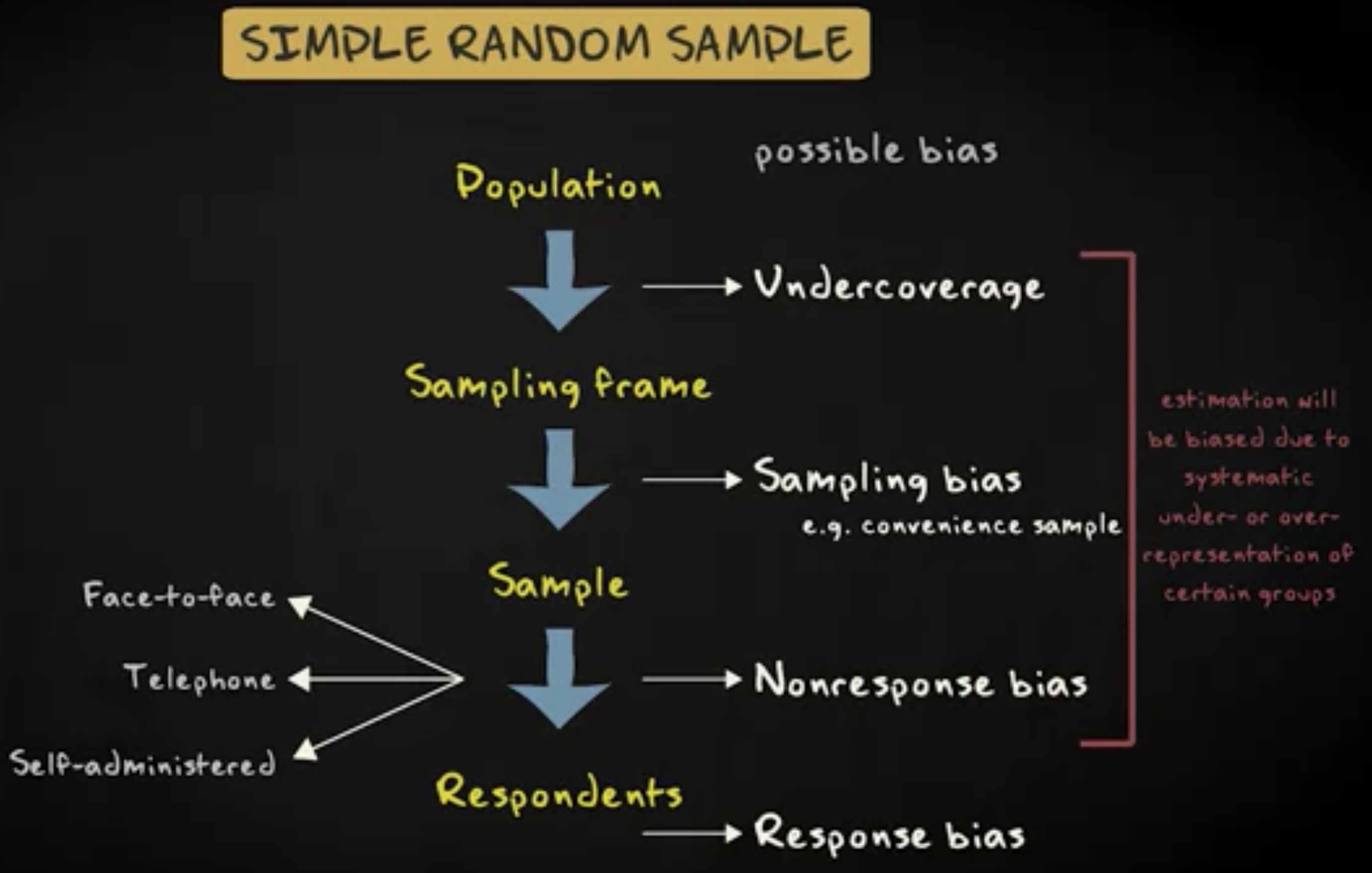
首先,你需要搞清楚总体是怎样的。我们已经知道,总体是全体伦敦学生。
第二步,得到全部主体的名单,我们称之为 抽样框 (sampling frame) 。想象伦敦有一个组织拥有所有学生的概况信息,包括他们的通信录细节。进一步的,这个组织愿意和你共享名单。你让计算机从名单中随机抽取 200 个学生。这样一来,你就得到了一个简单随机样本。
下一步是确定你如何触达你的 200 个调查对象。在面对面的采访中,你和调查对象在相同的房间,面对面提问。这么做到的好处是调查对象比较有可能参与,缺点是这样收集数据太昂贵了。另一个选项是通过电话采访,这么做开销小很多,但通常调查对象在电话上耐心有限,因此采访时间短暂。你还可以让调查对象填写问卷。因为他们可以在线完成调查,所以也是很便宜的选项,缺点是他们很可能不参与。
与此同时,你会遭遇各种形式的偏差。第一个是 覆盖偏差 (undercoverage) ,它指的是采样数据框没有囊括所有的个体。在伦敦学生的例子中,如果学生的清单不完整,就会发生这种偏差。有的学生没有机会被纳入样本。
还有 抽样偏差 (sampling bias) ,它指的是每个个体被纳入样本的机会不是均等的。当你的抽取做不到随机时,这种偏差就会发生。举个例子,如果你选择在街上随机接触人群,我们称为 任意抽样 或者 便利抽样 (convenience sample) 。它并非随机,因为有些人比其他人更少上街,他们被纳入样本的机会就更小。
其三,在你取得样本后,还有一种形式的偏差,它叫 无应答偏差 (nonresponse bias) 。某些被选中的主体可能拒绝参与实验,或者就是无法触达。还有些同意参与的调查对象只愿意回到特定的部分问题。
问题在于,这些不参与的情况可能不同于总体样本。无论它是覆盖偏差,抽样偏差或者无应答偏差。因为这些个人没有机会被抽样或者被抽样的机会更小,抑或这些个人拒绝回答某些问题,我们可能高估或者低估调查的目标。
简言之,我们的判断 (estimation) 会因某些分群的 表达不足 (under-representation) 或者 过表达 (overrepresentation) 出现偏差。
最后,还有 反应偏差 (response bias) 。在这个案例中,实际给定的反应是有偏差的。有可能,因为调查者问了某些前置的其他问题或者调查对象认为某些答案是社会不能接受的。有可能某个学生认为自己是个嬉皮士,但他认为调查者不喜欢嬉皮士于是就告诉调查者他不是。在我们的案例中,评估可能因为某些回应的 系统性误表达 (misrepresentations) 而出现偏差。
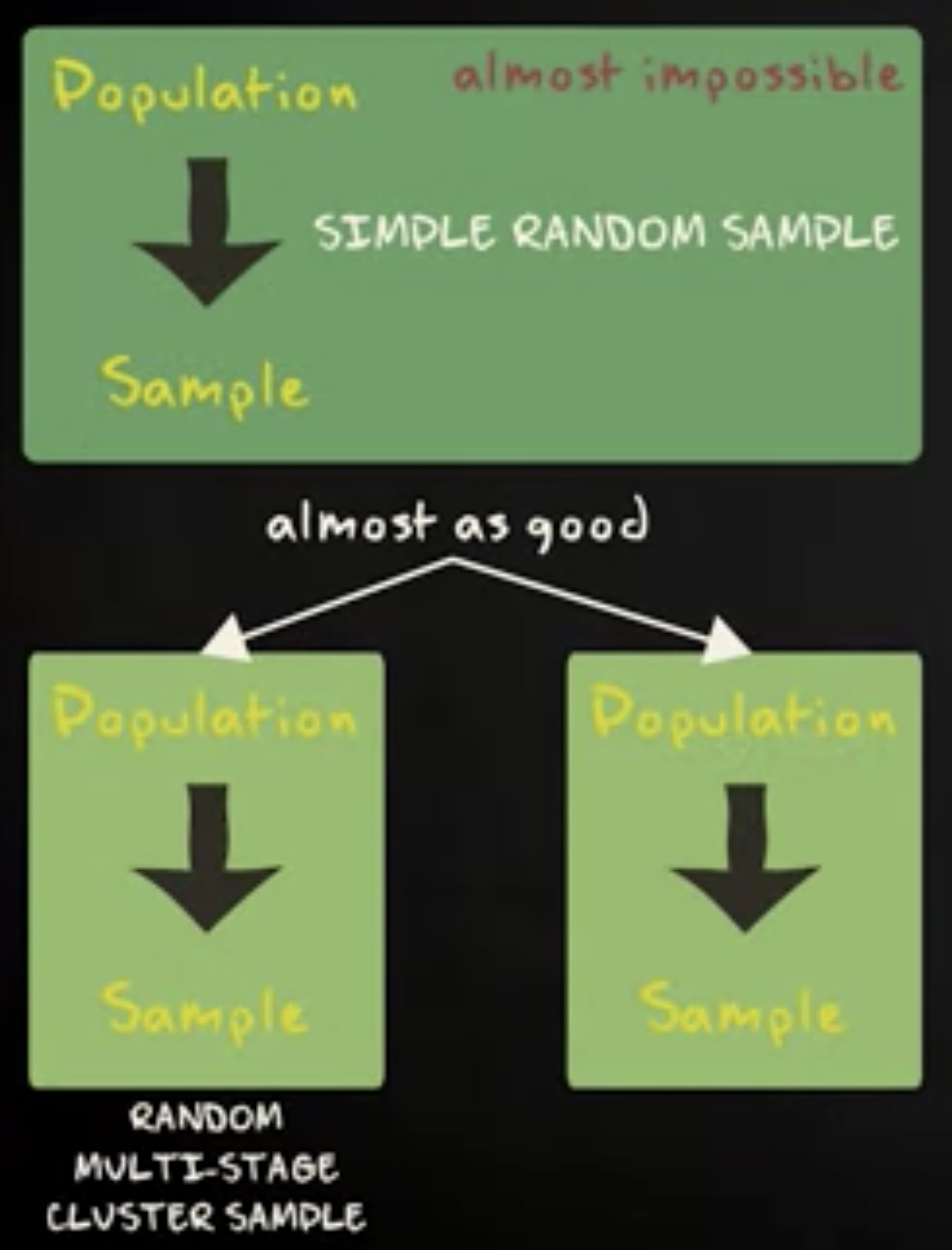
因此,在抽取样本时,你需要确保抽样是简单随机抽样,尽可能将各种形式的偏差降到最低。不过,很多情况下我们几乎不可能做到简单随机抽样。所幸,有另外两种随机抽样方式一样奏效。
在介绍它们之前,让我们先重温一下简单随机抽样的工作方式。如果你的总体中包含了所有的伦敦学生,你打算抽取 200 个学生的样本。你把所有学生的名字写在纸上。你把所有的纸放进箱子里,然后随机抽 200 张纸。这就是简单随机抽样。
第一个替代方案是 随机多阶段整群抽样 (random multi-stage cluster sample) 。它的工作方式如下:首先,你在总体中标识出大量的 整群 (cluster) ,比如,根据学生注册的不同的教育程序,每种程序用一个桶表示。把学生的纸按照注册的教育程序放入不同的桶中。接下来,你随机选几个桶,然后从这些桶中选取代表学生的纸,这样就得到了样本。多阶段整群抽样在你无法拿到很完整抽样数据框,或者简单随机抽样太昂贵时是一个很好的替代方案。
第二个替代方案是 分层随机抽样 (stratified random sample) 。现在,你将总体分成独立的组,这些组我们称为 层 (strata) 。例如,伦敦的各所大学,每个大学用一个盒子表示。你把学生的名字按照他们注册的大学放进不同的盒子里。接下来,你从每个盒子里随机挑出名字。所有这些名字就构成了你的样本。这种方法的好处是你可以确信样本中每一层都有足够的个体,缺点是你需要数据框,你还需要知道每个调查对象属于哪一层。
有一个重要的警告。大样本无法弥补糟糕的抽样步骤。如果你的样本不够随机,尽管你可以一直增加抽样数,你的样本也永远不会变得更好。假设你的样本是随机的,那大样本理论上总是更好的。不过,一旦你超过了某个临界点,样本量的增加对于总体参数评估准确度的影响就微乎其微了。

