欢迎关注微信公众号「Swift 花园」
抽样分布
研究人员经常会用样本来推断样本所处的总体。为了做这件事,他们需要用到统计世界中非常重要的一种概率分布 —— 抽样分布 (sampling distribution) 。
这一节中,我将向你解释抽样分布是什么。需要特别注意的是,抽样分布是帮助研究人员基于仅仅一个样本得出关于总体结论的桥梁。另外说明,在这节教程中,我们假装自己知道总体是什么样的。因为在研究实践中,我们通过永远都无法得知总体的全貌。这一步对于理解推断统计学至关重要。
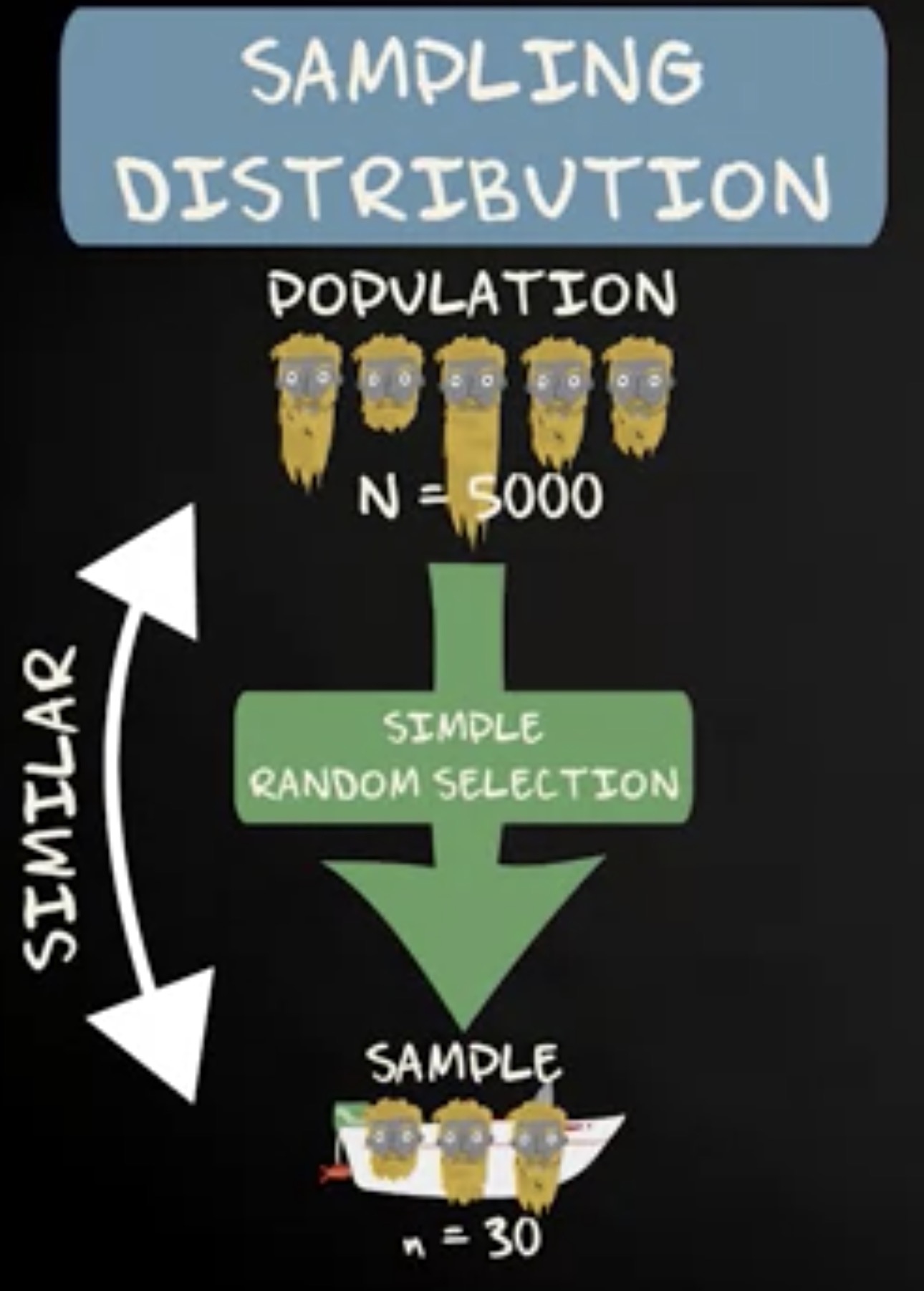
好吧,让我们进入正题。想象有一群北欧的嬉皮士组织了一场胡子节庆典。庆典将在挪威首都奥斯陆附近的一个小岛举行。显然,你能想到庆典的受众是有胡子的男性。组织售出了 5,000 张门票,并且提供了往来小岛的免费运送。

拥有门票的人将在奥斯陆的港口集结。组织将他们随即分装到运送乘客前往该岛的船上,每条船搭载 30 名庆典的粉丝。
现在,有一艘船迷失在挪威的群岛间。雪上加霜的是,手机网络崩溃了,因此组织无法联系上船长,船上的乘客也无法联系上组织。所有组织决定派出一些雇员去搜寻走失的船只。你正是其中的一名雇员。在历经里半个多小时的搜寻后,你看到一艘失事的船,上面有大约 30 个人。Yes,终于找到他们了。你正准备通过对讲机向组织报告失联船只已找到,这时你再看了一眼船上的乘客。你发现乘客都是一些带着小孩的家庭。这很奇怪,去胡子节的船上,不是应该都是一些随机选取的有胡子的成年男人吗?而不是一些带着小孩的年轻家庭。你认定这艘船不太可能是你要找的船,决定继续搜寻。果然,不久之后证明你的决定是明智的。你前面遇到的那艘船是一艘运送人们去另外一个岛上的家庭公园的船。
为什么要讲这个故事呢?这么说吧,如果你理解上面那个故事里 “你” 决策的原因,你就会理解抽样分布背后的基本思想。它是这样的,如果你从总体中抽取一个简单随机样本,那么它是不太可能强烈地区域于样本所处的总体的。在我们的案例中,人们正前往胡子节,他们构成了总体。一艘载有 30 个从总体中随机选取的人的船就是一个简单随机样本。
实际上,所有从奥斯陆港口前往庆典小岛的船都可以看做是一个简单随机样本。当然,每艘船都和其他船不一样,但大部分船都会包含大比例的有胡子的男人。不太可能有一艘船上都是各种年轻家庭。当然,有某些家庭参加胡子节是可能的,但是随机遇到一艘船,全部都是年轻家庭,则是非常不太可能发生的。

假设你决定测量每艘船的平均胡子长度。每艘船有 30 个人。想象 5,000 个庆典参与者的平均胡子长度时 10.3 毫米,即均值是 10.3 毫米。你还知道胡子的长度在总体中服从一个钟形的分布。在一艘船上,你可能遇到胡子平均长度是 9.4 毫米,另一艘则可能是 10.8 。但是,不太可能遇到一艘船,上面的人平均胡子长度是 3.4 毫米,或者 19.2 毫米。因为这些船上的人的胡子的平均值可以看作是样本的均值,我们用 $ \bar x $ 来注记。

现在想象你正看着三艘船,概率分布可能长这样:
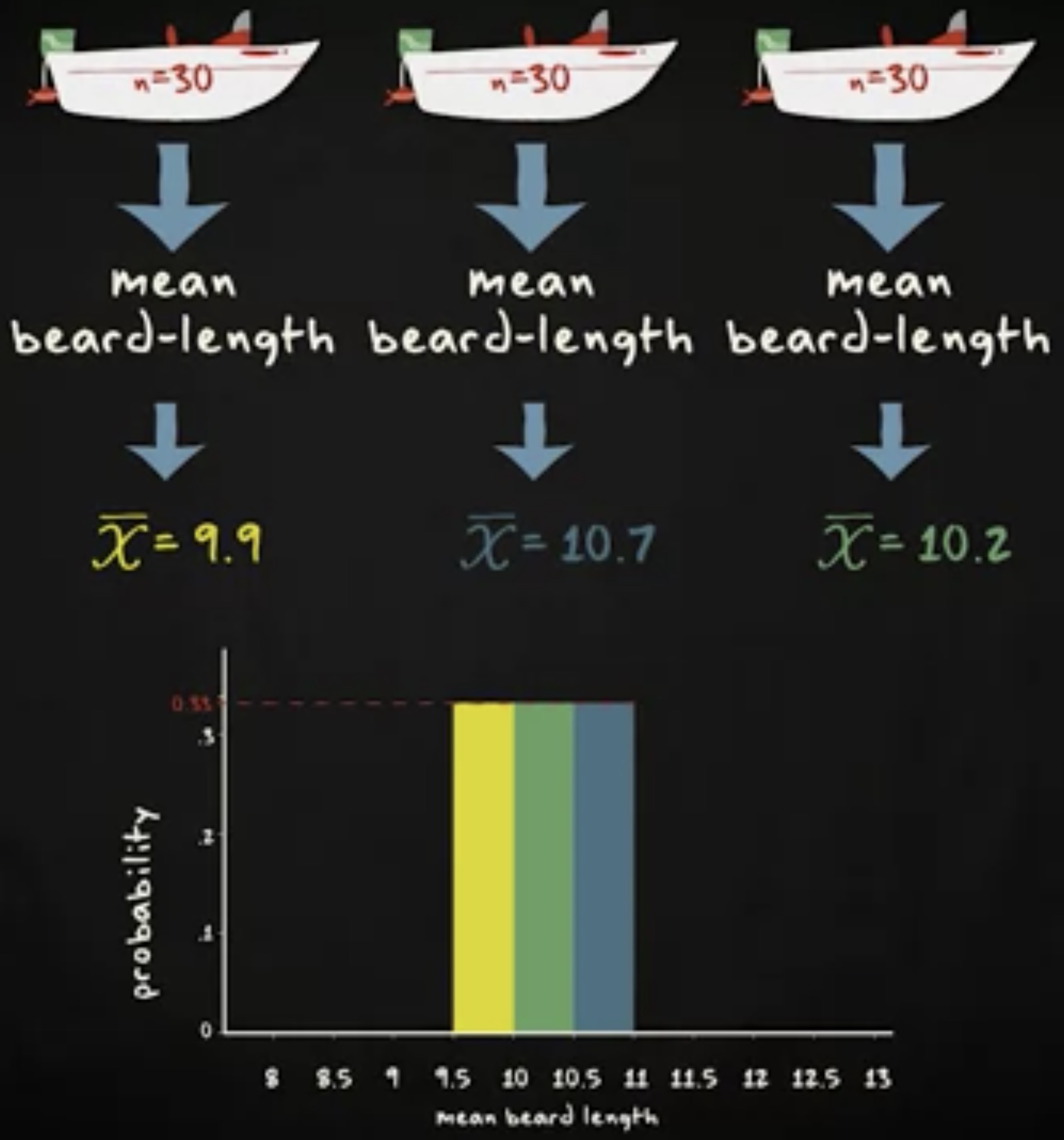
一艘船的均值是 9.9 ,一艘是 10.7 ,还有一艘是 10.2 。我们一共有三艘,所以每个均值的概率是 0.33 。现在想象有 17 艘船,40 艘船,100 艘船,你会发现胡子均值长度的分布会越来越接近钟形分布,并且,你会发现分布的均值接近 10.3 ,跟总体的均值一模一样。
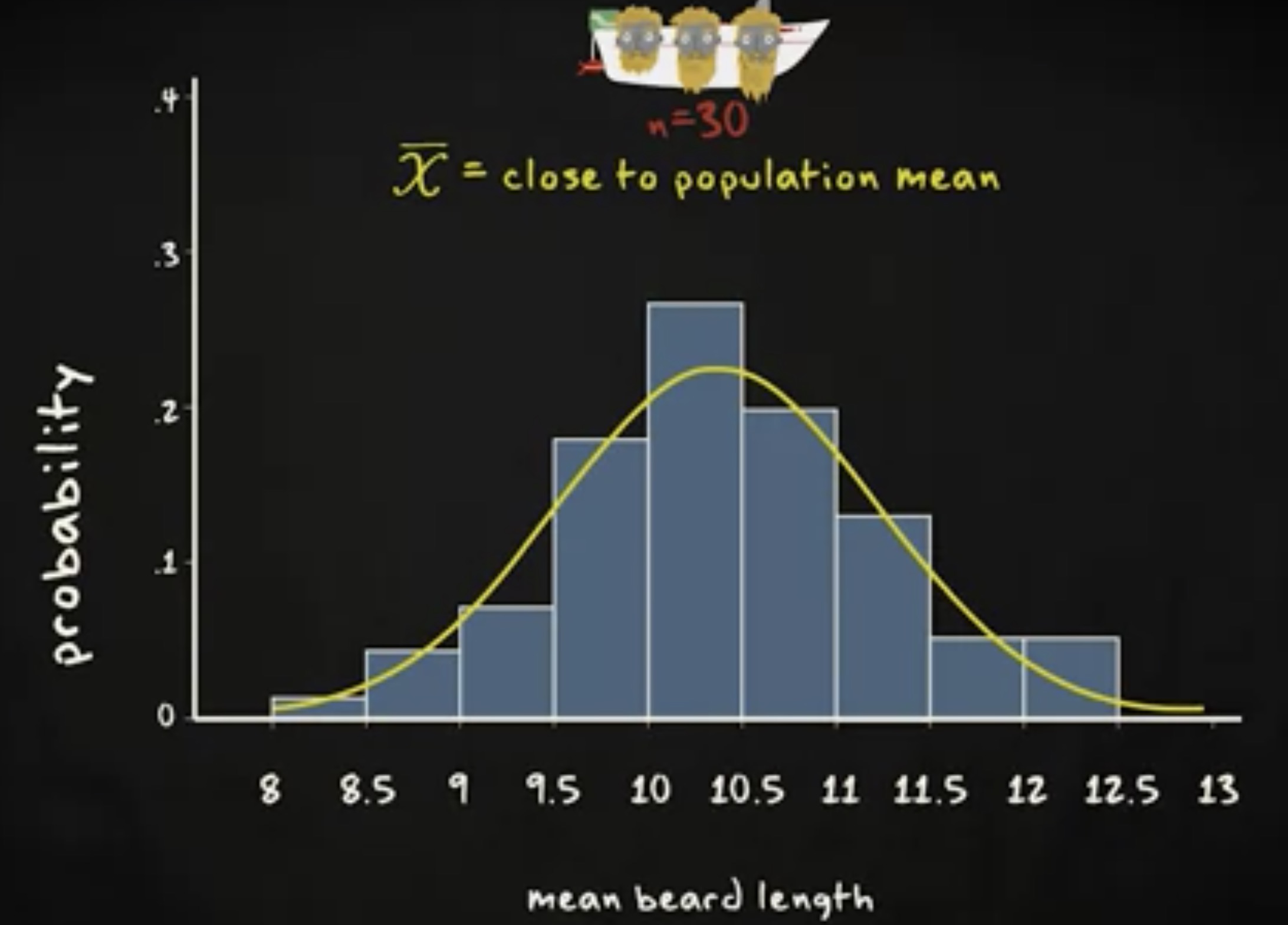
如果你仔细琢磨一下,就发现这并不奇怪。你会期望,在绝大多数情况下,样本的均值和总体的均值接近。某一艘船的均值可能高一点,另一艘船的均值可能低一点。但是,当你看到许多船时,你会期望所有这些不同船的均值的均值,就等于总体的均值。

现在,想象你的总体包含了所有的挪威男人。你知道这个总体的胡子长度均值是 1.22 毫米,并且变量服从一个钟形分布。如果你抽取一个 30 人的简单随机样本,你会发现均值接近总体均值,比如 1.34 毫米。你再抽取另一个随机样本,均值可能是 1.19 毫米,也很接近总体均值。如果你重复五次,你会得到五个不同的值,但是都很接近总体的均值。
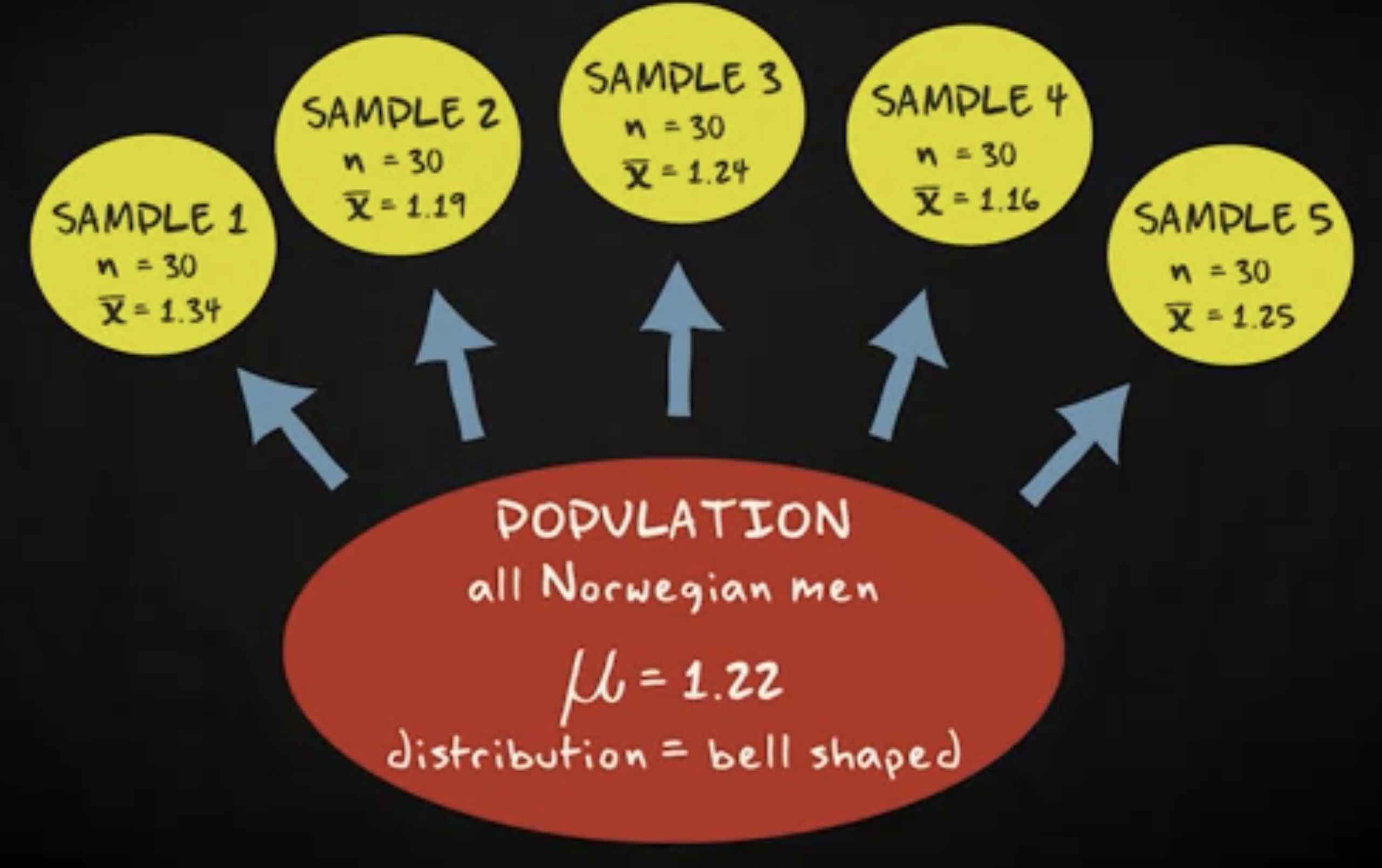
当我们可以抽取无限多个样本时,分布将会是一个完美的钟形,均值是精确的 1.22 毫米,跟总体均值一样。我们把这种分布称为 样本均值的抽样分布 (sampling distribution of the sample mean) ,它是这样一种分布:你从总体中无限抽取样本,计算所有样本的均值。

目前为止,你应当意识到,在实际的研究中,我们不可能从某个总体中抽取无限多的样本。但是,你需要知道,如果我们能这么做,这个分布的均值将等于总体的均值,这正是我们把这个分布称为样本均值的抽样分布的原因。不要把这个和样本或者数据分布混淆在一起,这只是实际抽取的一个样本的分布,只针对实际收集的数据而言。
中心极限定理
如果你从钟形分布的总体中取无限个样本,来自这个无限个样本的均值分布将会是钟形的。并且这种样本均值的分布将会和总体均值完全一样。我们将此分布称为样本均值的抽样分布。
在这一节中,我将讨论 中心极限定理 (central limit theorem) —— 推理统计学中,最重要的公式之一。

中心极限定理表明,假设样本量足够大,样本均值 $ \bar X $ (x 的均值) 的抽样分布近似正态分布,即使这个变量在总体中并不是正态分布。这不是很神奇吗?不用理会变量在总体中是如何分布的,样本均值的抽样分布总是如此,总是近似正态分布,只要样本量足够大。作为足够大的指导,通常使用 30 或更大的样本。
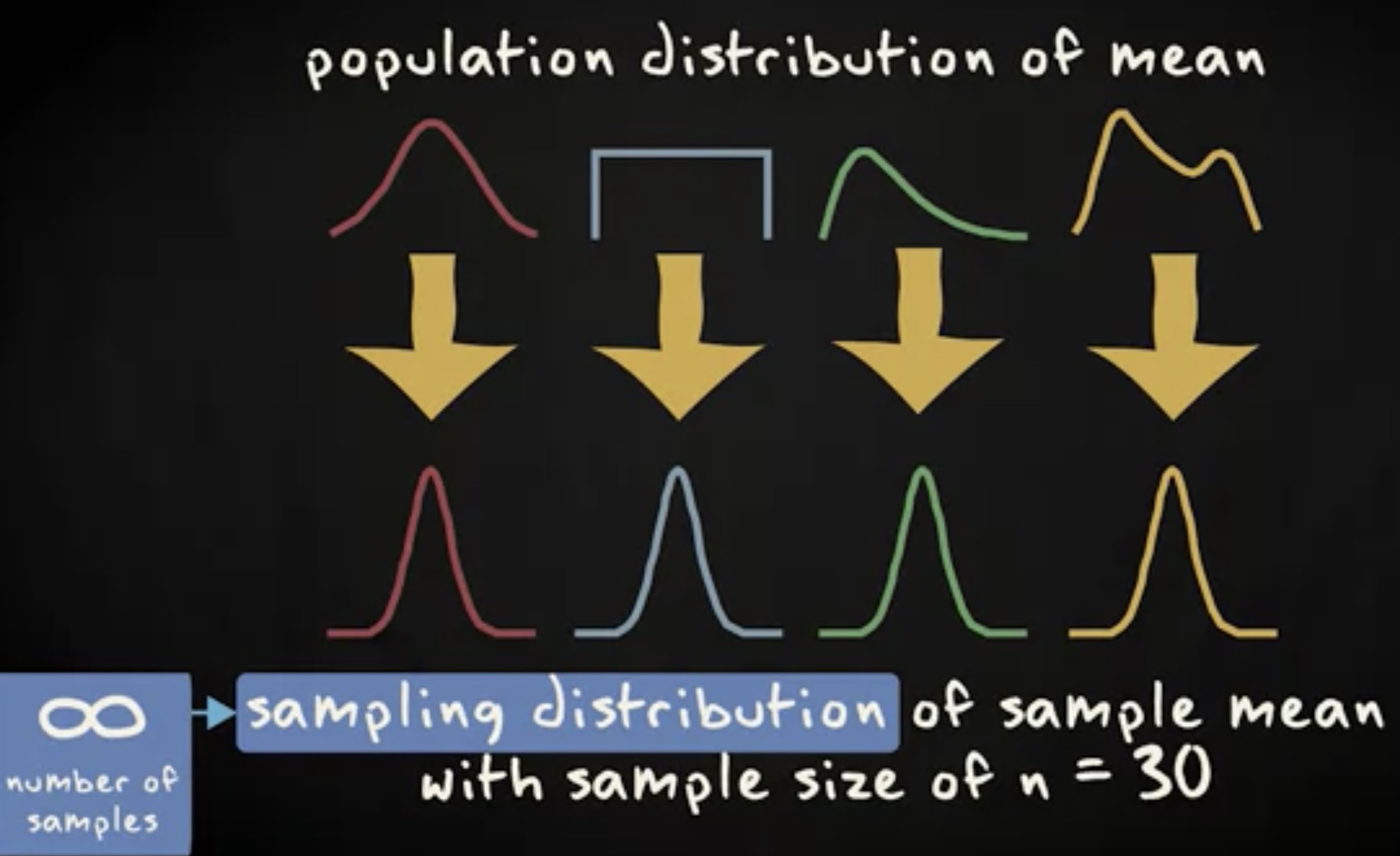
你们可以看这些总体分布可能的形状。这是当你取样本容量 n=30 时,样本均值的抽样分布图。记住,这意味着你从总体中抽取了无数个由 30 个调查对象组成的随机样本,在分布中显示所有生成的样本均值。
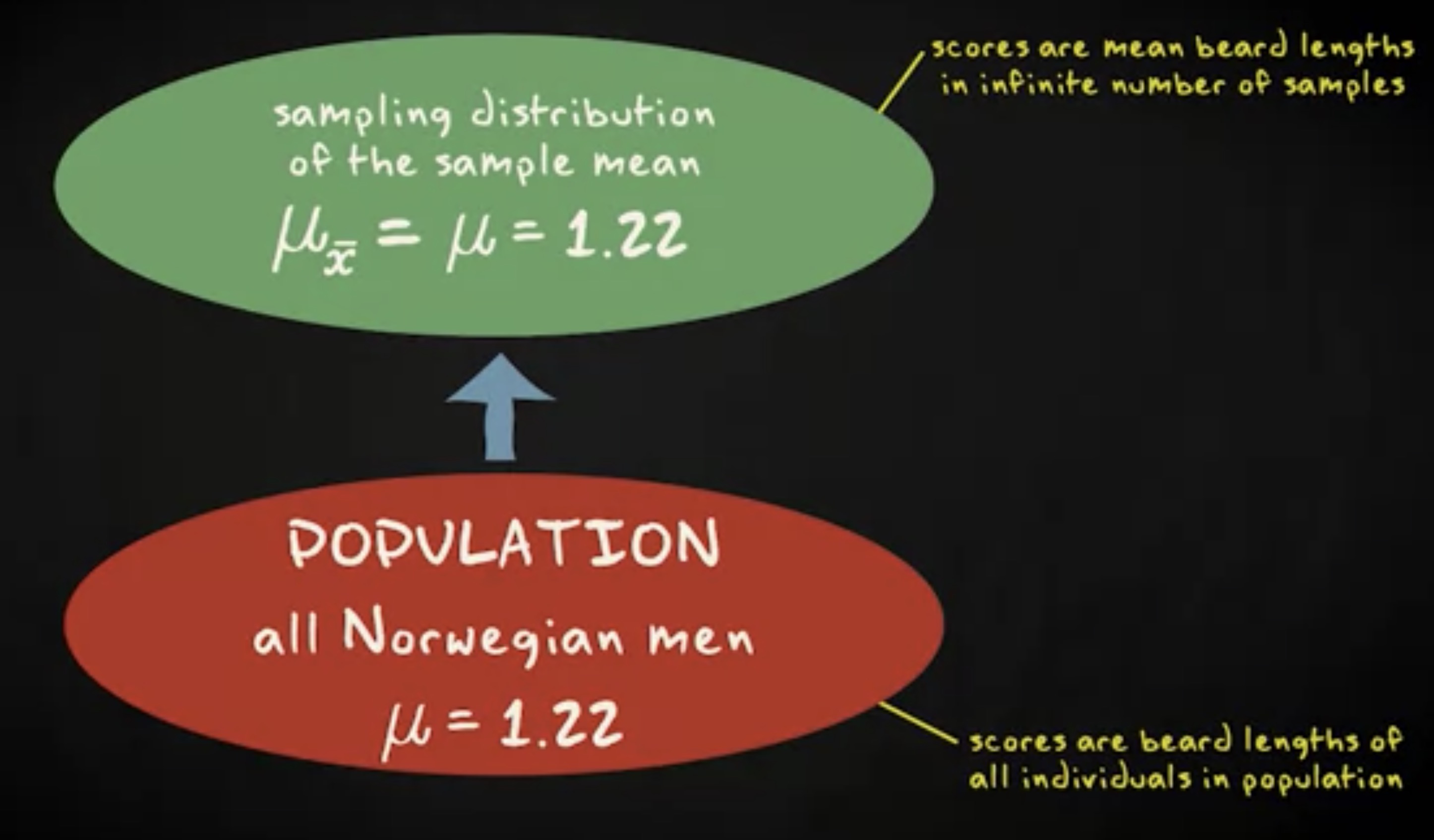
你应该意识到,在实践中,根本不可能抽取无数个样本。但是,好消息是根本不需要抽取多个样本来确定样本分布的形状。 因为如果它是正态分布,你可以通过两个参数来描述它的形状,即均值和标准差。因此,估计这两个参数就足够了。正如我之前告诉你的那样,抽样分布的均值等于总体分布的均值。我们可以这样表示,$ \mu{\bar x} = \mu $,$ \mu $ 代表总体的均值,$ \mu{\bar x} $ 代表样本均值的均值。
想象你对挪威男人的平均胡须长度感兴趣。总体包括所有挪威男子,$ \mu $ 是总体的平均胡须长度。我们假设它是 1.22 毫米。对于样本均值的均值,如果我们从总体中抽取无数个样本,并记下每个样本中的平均胡须长度,我们就会得到这个分布的平均值,等于总体均值 1.22 。$ \bar X $ 是用来强调抽样分布中的分数是样本均值,而不是个体的分数。换句话说,总体分布的平均值是所有挪威男性的胡子长度得分的平均值。抽样分布的均值是从该人群中抽取的无限多个样本的样本平均值。
如果我们知道总体分布如何,我们可以轻松的计算出样本的标准差。抽样分布的标准差的符号化是 $ \sigma_{\bar x} = \frac {\sigma}{\sqrt {n}} $ 。添加 $ \bar x $ 下标是为了表明我们正在谈论抽样分布的标准差,其中分数是样本均值,或者换句话说,$ \bar x $ 的 $ \mu $。$ \sigma $ 代表总体的标准差, n 代表样本的大小。此公式表明抽样分布的标准差受两个特征影响。首先,它受总体标准差的影响,假设 n 等于 30 ,你的总体标准差是 1 ,你的抽样分布的标准差等于 1 除于根号 30 ,等于 0.18 。如果你的总体标准差增加至 2 ,样本的标准差变成 2 除于根号 30 ,即 0.37 ,如果你的总体标准差变成 3,样本的标准差变成 0.55 ,等等。
所以,如果总体分布的的标准差增加,抽样分布的标准差也会增加。换句话说,总体方差越大,样本均值的方差越大。这在直觉上是合理的,对吧?如果你从人群中胡须长度差异很大的人群中抽取 30 个受试者的各种样本,你可以预期这些样本的相互之间的差异比你从几乎没有差异的总体中抽取各种样本的差异更大。你的抽样分布的标准差,也会受到样本容量的影响。再看看这个公式。假设总体标准差等于 2 。现在,如果 n=30 ,$ \sigma{\bar x} $ 等于 2 除于根号 30 ,等于 0.37 。 如果 n=100 ,你的抽样分布的标准差将变为 2 除于根号 100 ,等于 0.2 。如果 n = 500 ,你的 $ \sigma{\bar x} $ 变为 0.09 。
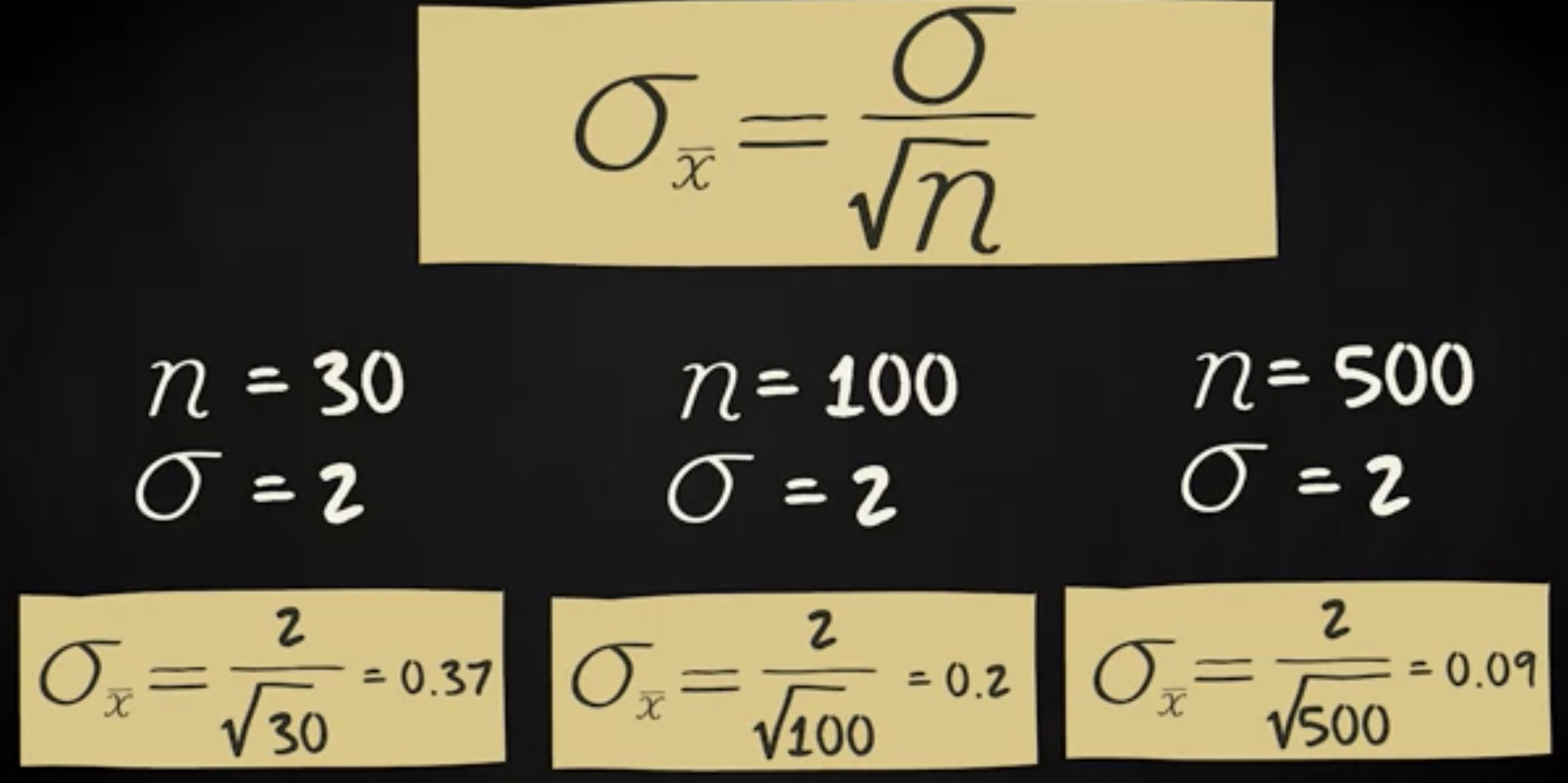
这表明,一个更大的样本量导致抽样分布的标准差更小。这在直觉上也是合理的。如果总体中的挪威男性的平均胡子长度为 1.22 毫米,你只有两个受访者作为样本,找到一个更高的平均值并不奇怪。如果你抽取了五个样本,你的样本均值是看起来像这样。
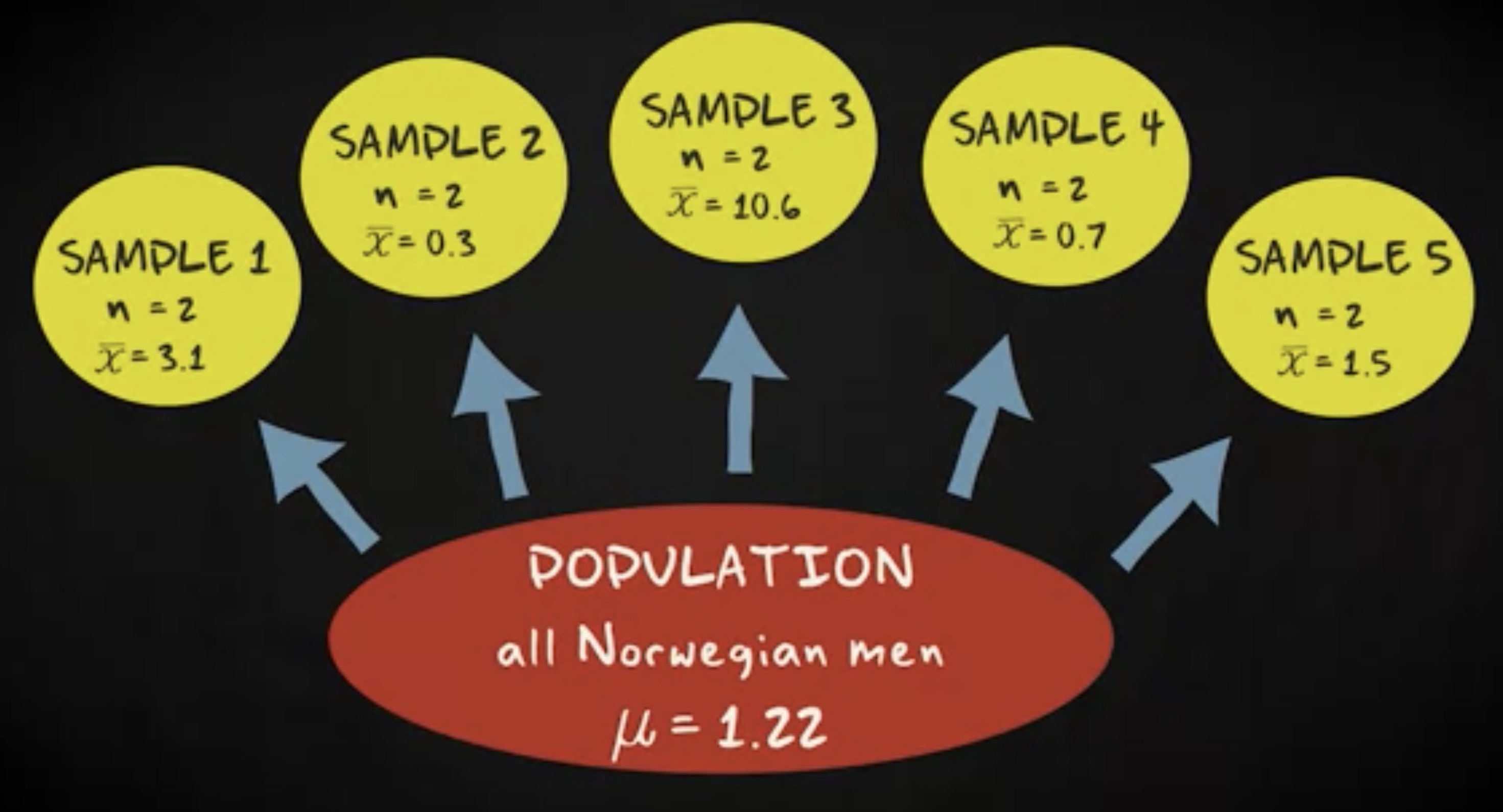
现在,想象一下你抽取了一个 1000 个受试者的样本,这个样本的均值不太可能是 5 或者 10 毫米。毕竟,长胡子的人会被完全没有胡子的人抵消。如果你抽取五组样本,样本均值可能看起来像这样。
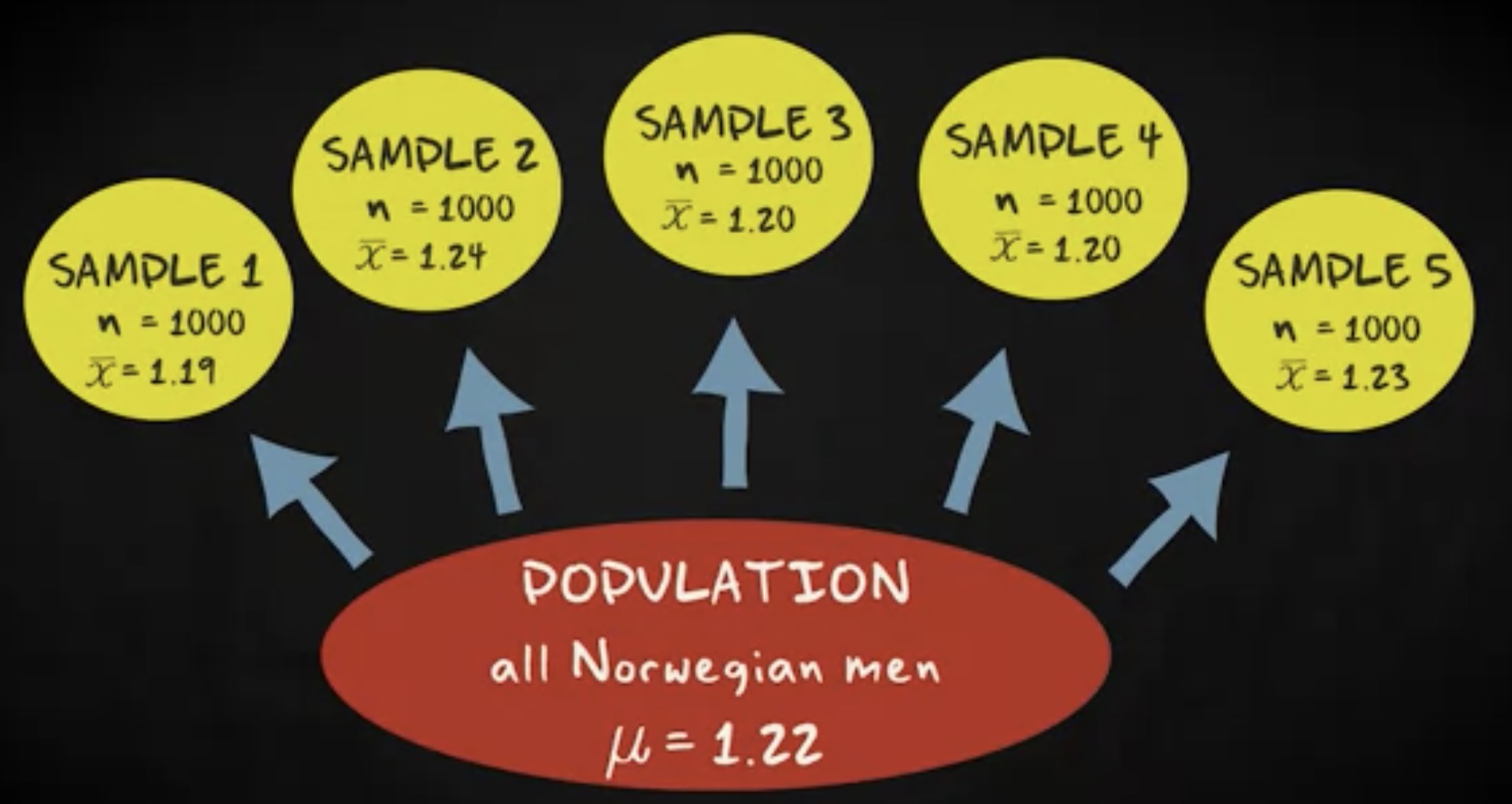
它们都将非常接近总体平均值 1.22 毫米。所以你的样本容量越大,样本均值越接近总体均值,样本分布的标准差越小。
小结
- 中心极限定理告诉你:无论变量在总体中分布如何,只要样本容量至少为 30 ,样本平均值的抽样分布都近似正态分布。
- 抽样分布的均值 $ \mu{\bar x} $ 等于总体均值 $ \mu $ ,抽样分布的标准差 $ \sigma{\bar x} $ 等于总体分布的标准差 $ \sigma $ 除于 $ \sqrt {n} $。
三种分布
许多社会的、政治的以及宗教的团体有它们自己的神圣文字。嬉皮士,也有它们自己的 “圣经”,这是一本名叫 “On the Road” 的书。这一节中,我们对于纽约市的嬉皮士花了多少时间读这本书感兴趣。
假设我们知道总体,所有嬉皮士读这本书的平均时长是 943 分钟。我们还知道,总体的标准差等于 212 分钟。你从总体中做简单随机抽样抽取了 200 个受试者。这个样本中的平均阅读时长是 867 分钟,标准差 188 分钟。
这一节,我将介绍对于研究项目十分重要的三种分布 —— 总体分布 (population distribution) ,样本分布 (sample distribution) , 抽样分布 (sampling distribution) 。我将向你展示,如果计算针对特定分数的选择性个体的概率。
第一个分布,总体分布,它看起来像这样,近似钟形,均值 943 分钟,标准差 212 分钟,主体是纽约的嬉皮士们。
第二个分布,数据分布或者是样本分布,它是样本数据的分布,看起来像这样。它跟总体分布一样,近似钟形,均值 867 分钟,和总体均值 943 分钟相差不大。标准差 188 分钟。
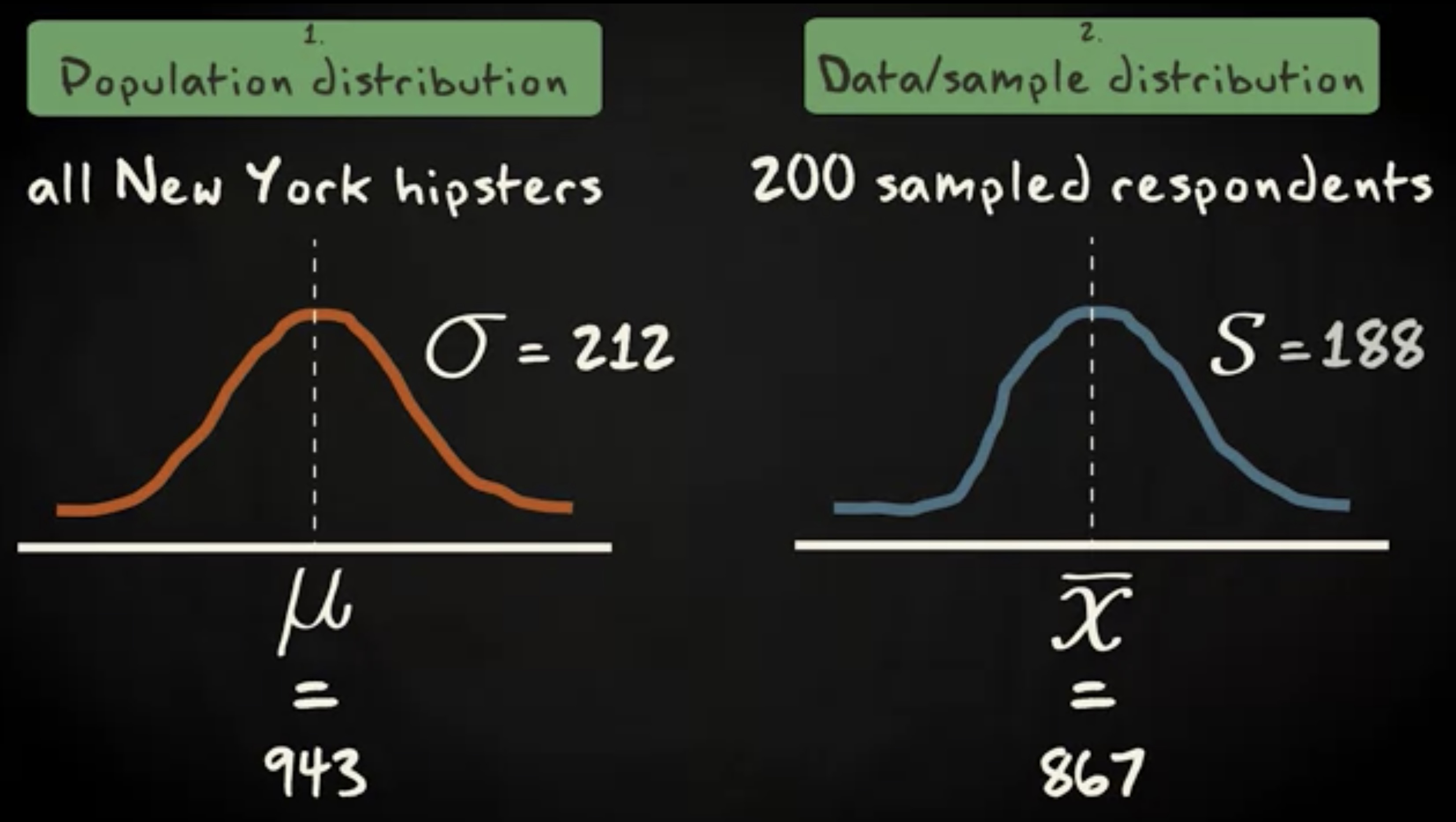
注意,样本统计里采用罗马字母注记,而总体里采用希腊字母注记。
第三种分布,样本均值的抽样分布,它就像下面这样:
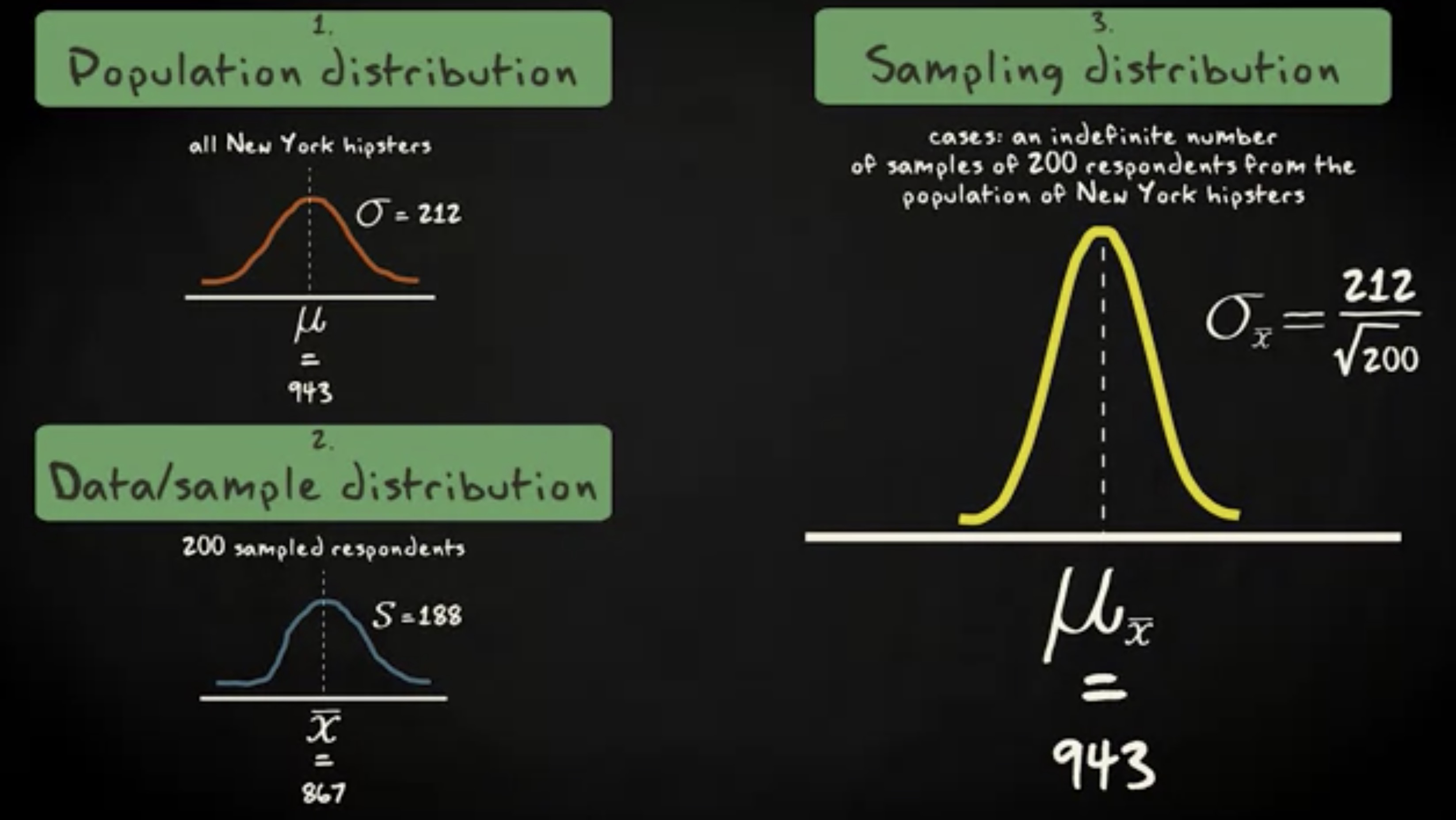
根据中心极限理论,它是正态分布的。在这个分布中,主体不是分布中的个体,而是来自纽约嬉皮士的 200 个受试者样本的一个不确定的数字。样本均值的抽样分布的均值,是这些不确定样本均值的均值。具体的数值,等于总体分布均值的数值,即 943 分钟。为了说明我们正在讨论的是抽样分布,我们添加 $ \bar x $ 下标来表明是样本均值的均值而不是个体分数的均值。抽样分布的标准差,等于总体标准差,除以 n 的平方根,即 212 ,除以 200 的平方根,得到 15 。
你需要记住的是,第三个分布是一个理论上的分布。我们并不实际地收集无限多的样本。那是不可能做到的,也不必做到。因为只要我们知道总体的均值和标准差,我们就能知道抽样分布长什么样。正态分布的一个大好处是,我们可以通过把原始分数变换成 z 分数,以及引入 z 表格,找出概率。
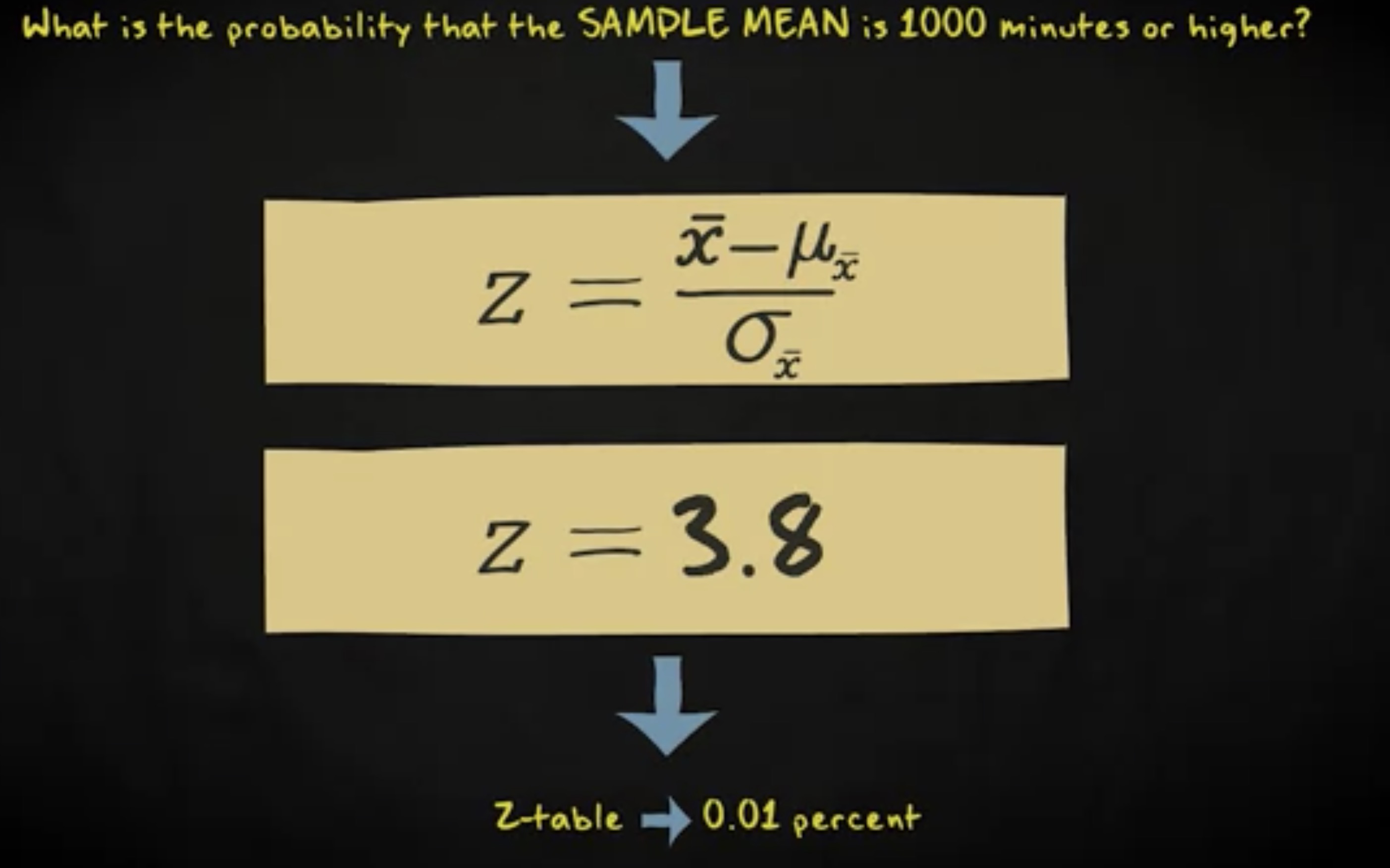
现在,想象你从总体中选择一个随机样本,这个嬉皮士阅读时长大于等于 1000 分钟的概率是多大呢?
首先,我们需要知道一个嬉皮士阅读那本书的时长等于 1000 分钟距离均值有多少个标准差。我们在总体中计算这个人的 z 分数,z 分数是 1,000 减去 943 ,除以 212 ,等于 0.27 。我们感兴趣的是这个值右边的区域。查询 z 表格,我们发现选中一个阅读时长大于等于 1,000 分钟的嬉皮士的概率是 39% 。现在,想象我们抽取 200 个嬉皮士。这个样本均值大于等于 1,000 分钟的概率是多少?千万注意,这是一个完全不同的问题。我们不是在讨论从总体中选取一个特定的人,而是在讨论基于总体中的特定样本的统计学。因此,我们不用总体分布,而是样本均值的抽样分布。通常,过程是相同的,只不过我们用的是不一样的均值和标准差。这里, z 分数计算过程如下。我们从感兴趣的均值,即 1000 ,减去抽样分布的均值,即 943 ,然后除以抽样分布的标准差,即 212 除以 200 的平方根,即 15 。因此, (1000 - 943) / 15 ,最后得到 z 分数是 3.8 。查询 z 表格,我们发现抽取一个样本的平均阅读时长均值大于等于 1,000 分钟的概率是 0.01% 。
小结
- 决定选用哪种分布时,需要十分小心。如果你是对选择的独立个体感兴趣,应当使用总体分布;但如果你是对选择的样本感兴趣,应当使用抽样分布。在实际的研究实践中,混淆总体和抽样分布几乎不可能发生。因为你永远无从知道总体的全貌。你唯一可以确定的是你的样本长什么样。
接下来,我们会学习如何在缺少总体分布信息的情况下,利用好抽样分布。

