欢迎关注微信公众号「Swift 花园」
抽样分布比例
想象你住在巴黎,你知道所有的学生中有 0.10 的比例把自己看做嬉皮士。你想要知道这个比例的抽样分布是什么样的。注意,在这里计算总体均值是没有什么意义的。因为你感兴趣的变量是一个二元标量。学生们可以选择认定自己是或者不是嬉皮士。均值和这样一个二元变量无关。
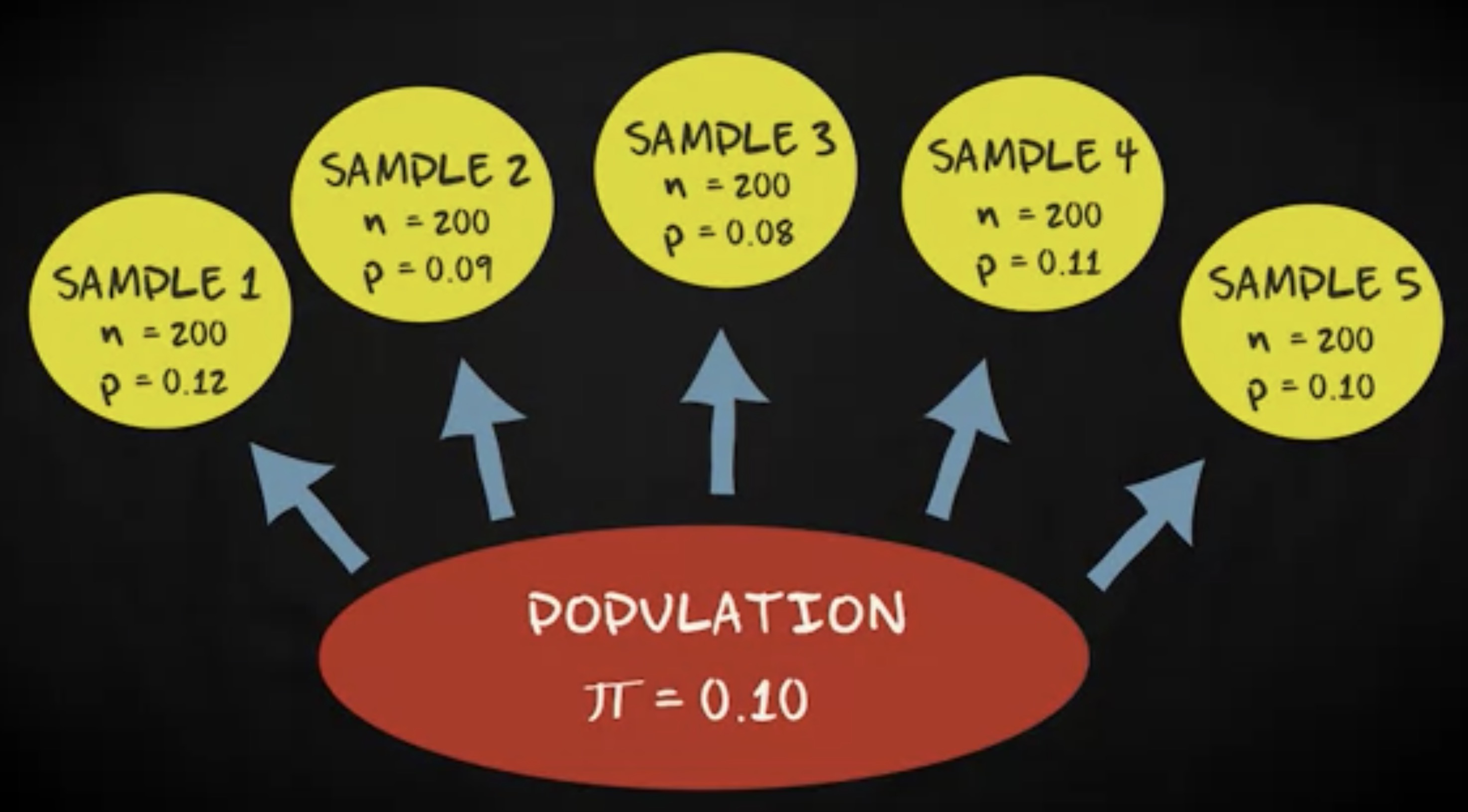
在本节教程中,我将解释一个总体比例的抽样分布是长什么样。你知道巴黎有 10% 的学生认为自己是嬉皮士,这意味着总体比例,用 $ \pi $ 注记,等于 0.10 。现在想象我们从这个总体中抽取 200 个学生。样本的比例,用 $ p $ 注记,将会是一个接近 0.10 的数字,比如 0.09 或者 0.12 。
如果抽取了 5 组样本,样本比例可能如下:
这样样本比例的直方图可能如下:
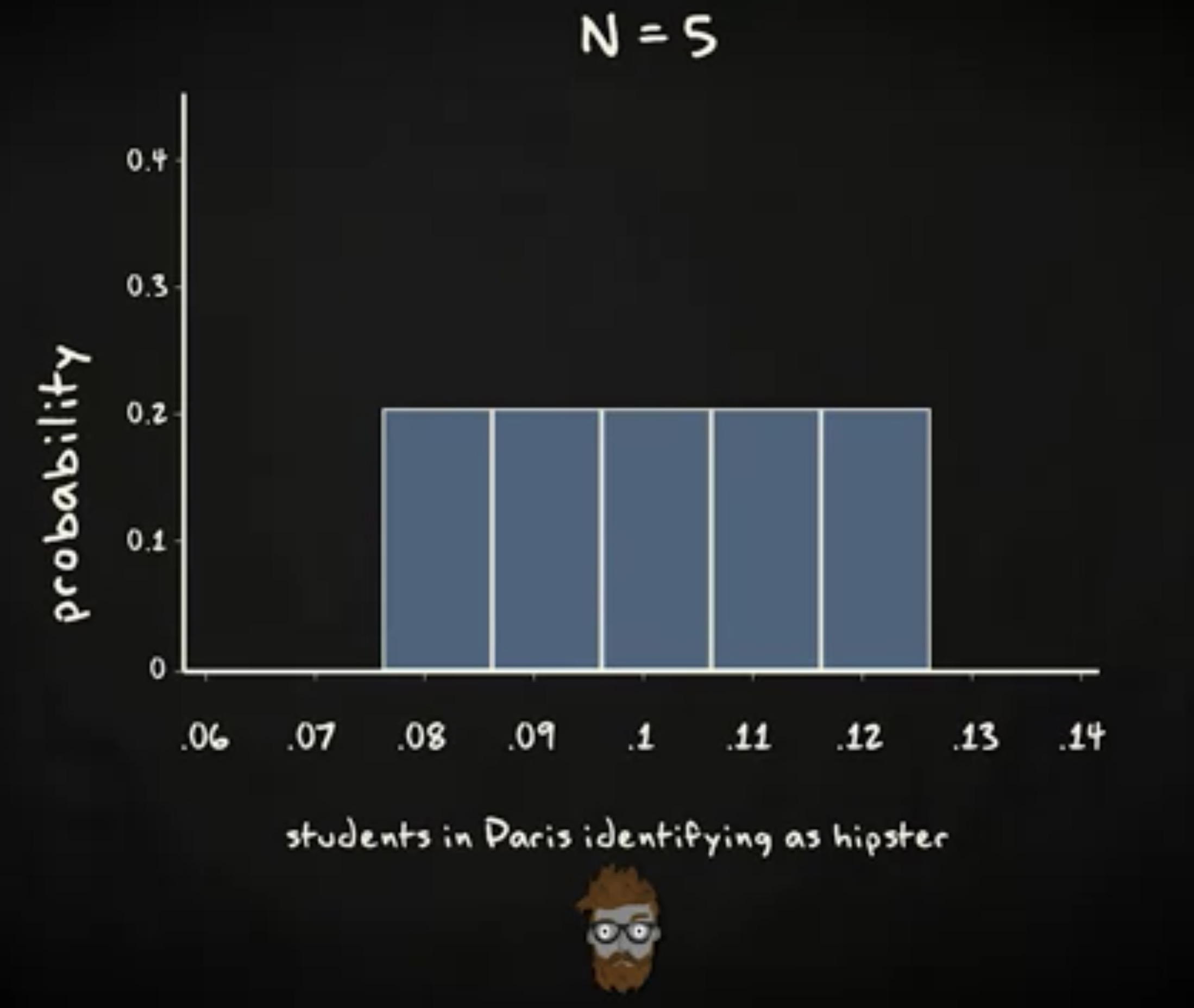
有五个值,全部都出现一次,它们的概率都是 0.2 。现在,你抽取 25 组样本,分布可能如下:
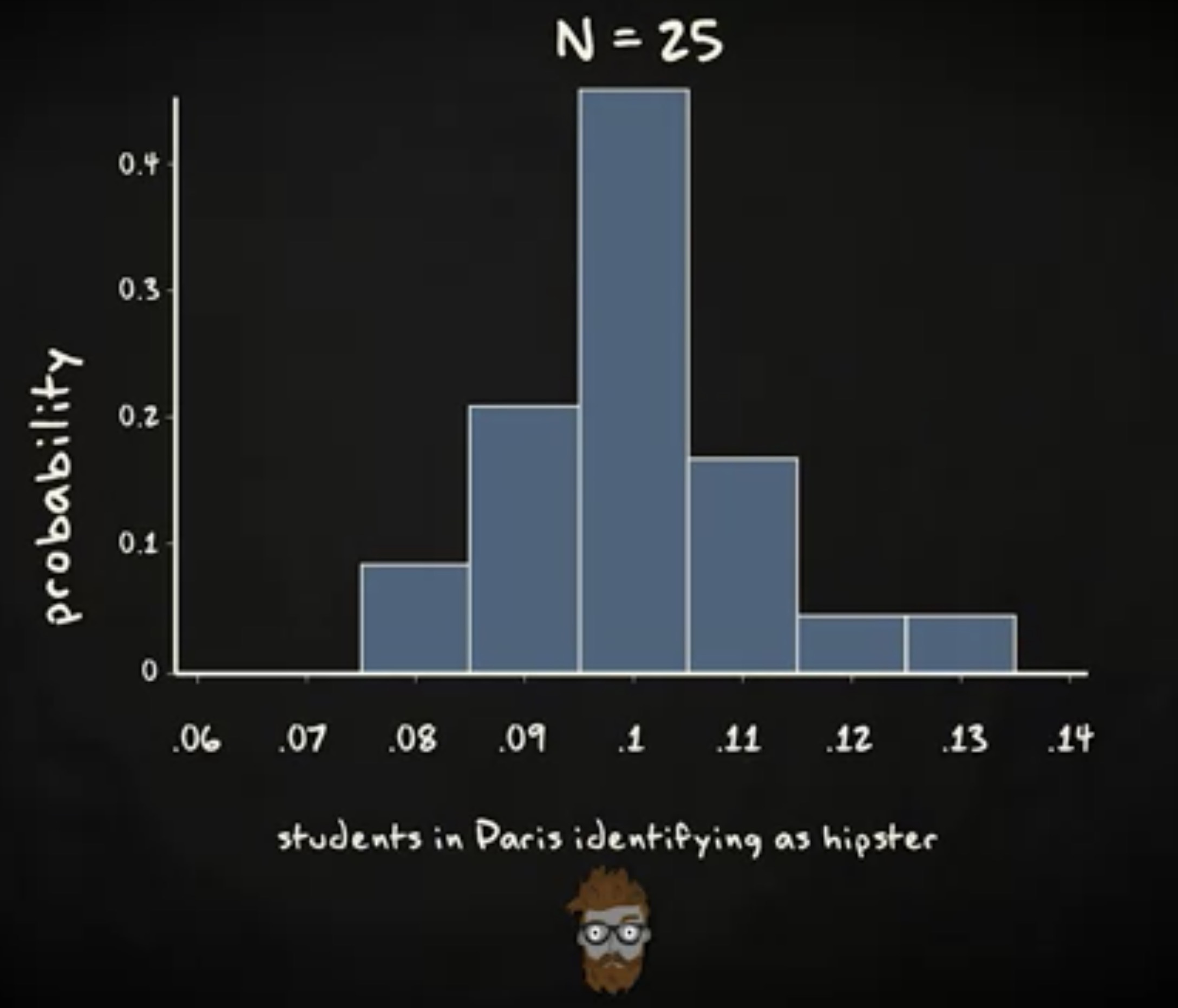
抽取 50 个样本,分布如下:
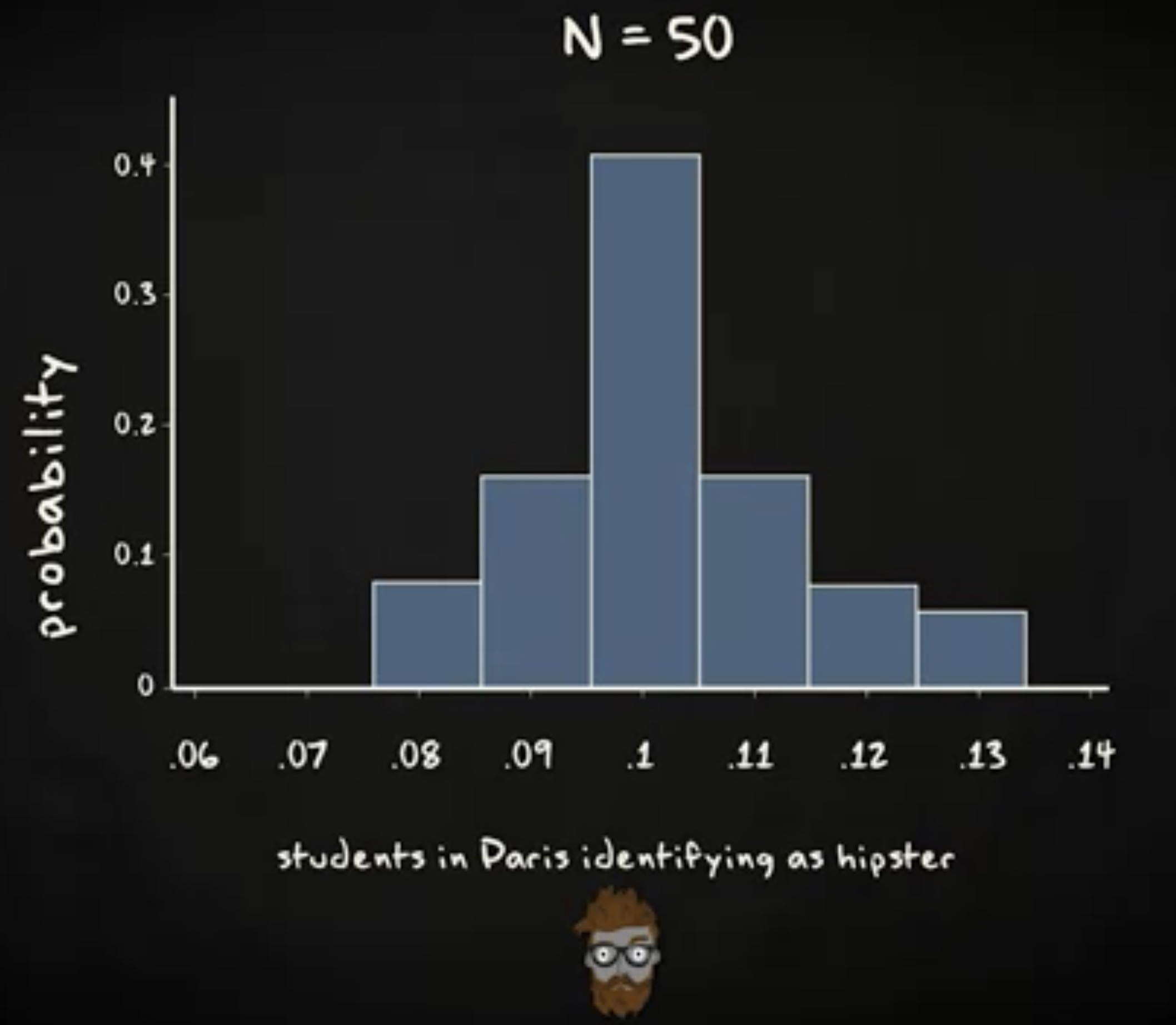
无限多组样本,分布如下:
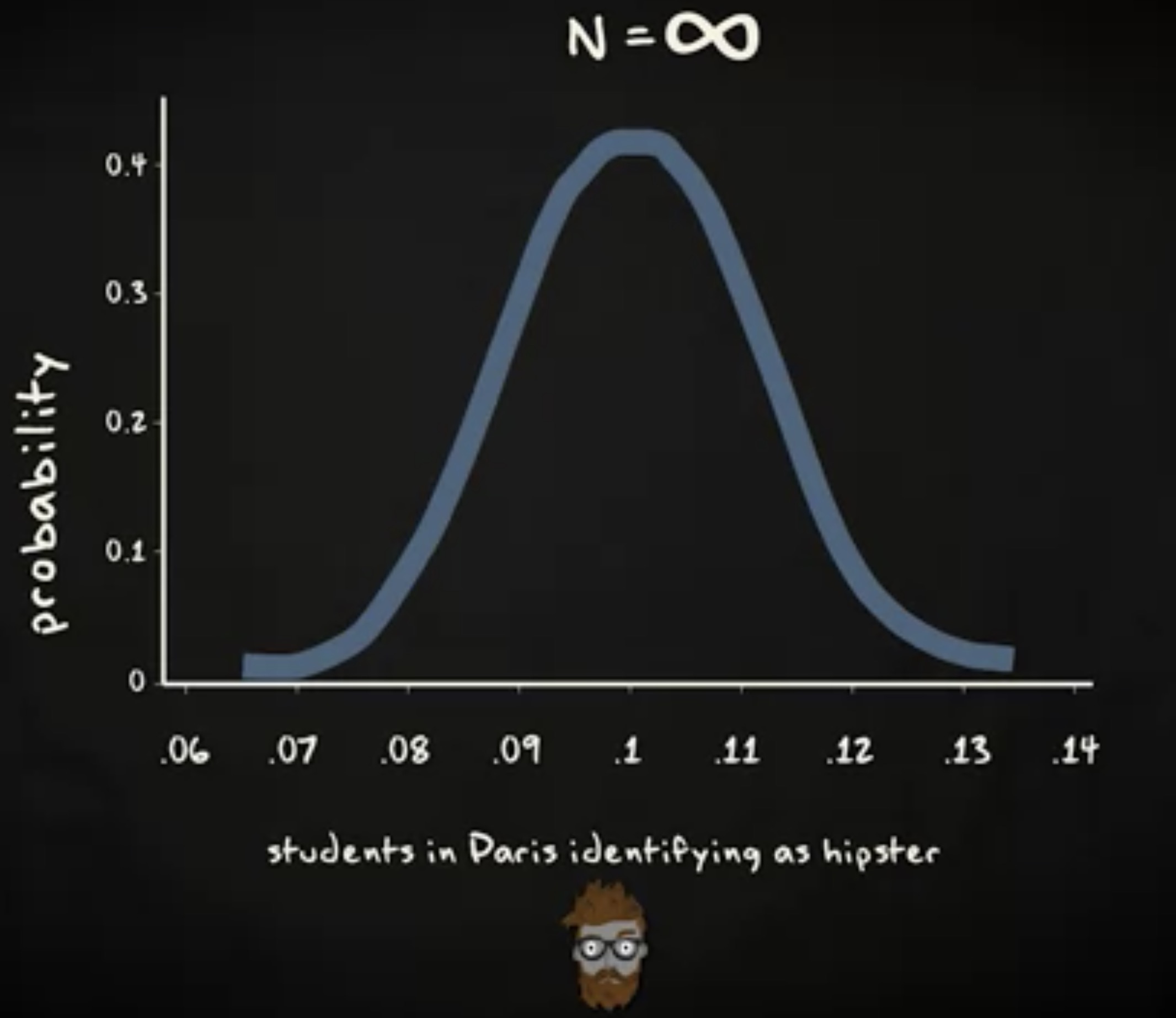
这是样本比例的抽样分布,分布的均值是 0.10 ,等于总体的比例。为了表明我们是处理抽样分布的均值,均值被注记为 $ \mu_p $ ,下标 p 是为了说明我们正在处理的分布的分数不是个体的分数,而是样本比例。如你所见,逻辑上和样本均值的抽样分布一模一样。
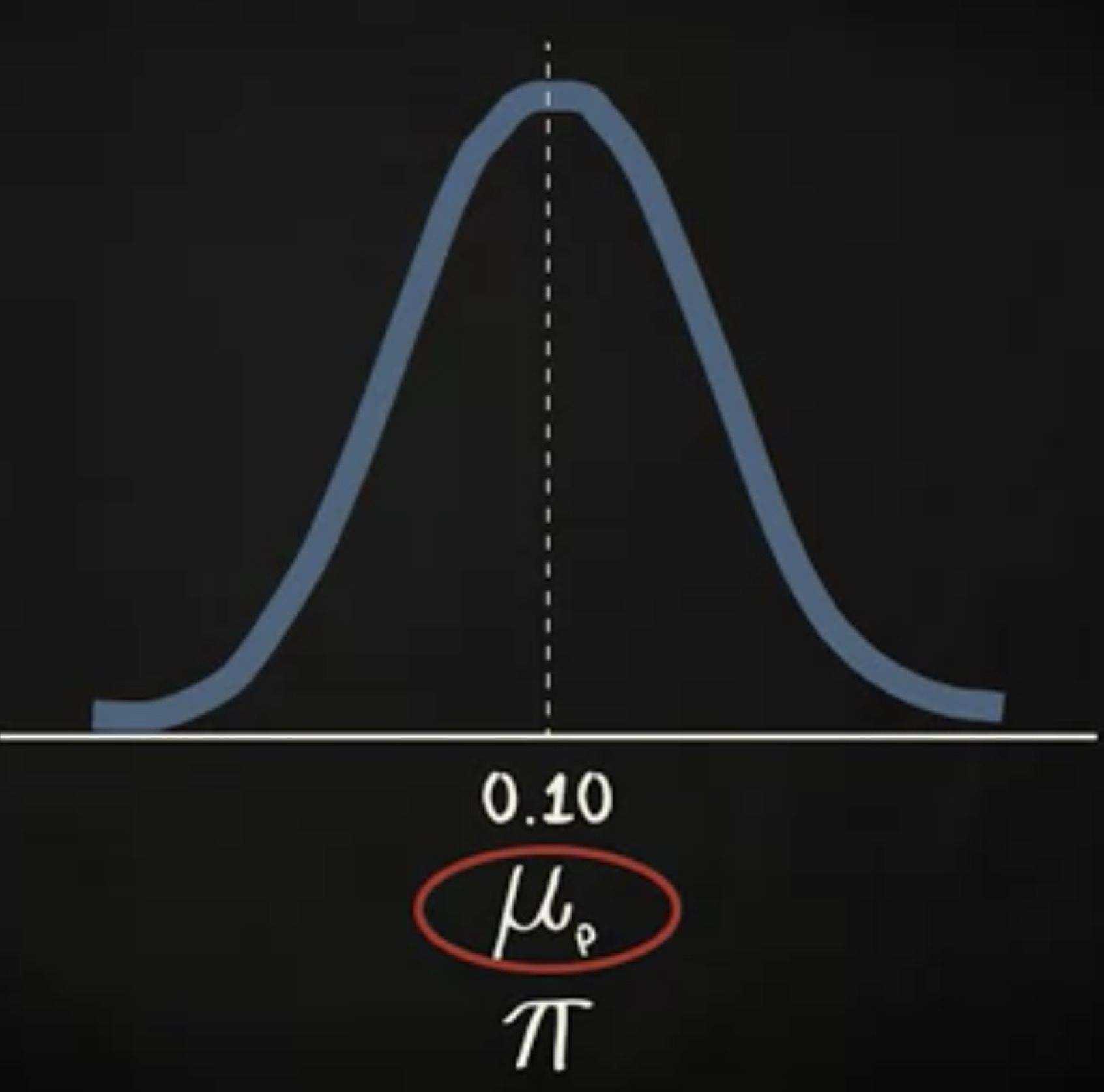
在样本均值的抽样分布案例中,如果总体本身是正态分布或者样本容量足够,那抽样分布是近似钟形的。通用最小需要 30 个样本数。在样本比例的抽样分布中,只有当你拥有至少 15 个正向的 case 以及至少 15 个负向 case 的前提下,你才能确信分布是钟形的,即至少 15 个嬉皮士和 15 个非嬉皮士。公式表达如下:
这对于我们的例子意味着什么呢?首先,样本容量和总体比例的乘积必须大于等于 15 。在我们的案例中,即 200 乘以 0.10 ,等于 20 个嬉皮士。其次,总体比例和 $ 1 - \pi $ 的乘积必须大于等于 15 。在我们的案例中,即 200 乘以 (1-0.10),等于 200 乘以 0.90 , 等于 180 个非嬉皮士。 因此我们可以下结论,抽样分布将会是钟形的,因为 20 和 180 都大于 15 。有一个相当直接的公式可以计算样本比例的抽样分布的标准差。我们以 $ \sigma_p $ 注记标准差,你知道 $ \sigma $ 代表标准差,而添加的 p 则表明我们正在讨论的是样本比例的抽样分布。 为了计算这个标准差,公式如下:
在我们的案例中,标准差算出来是 0.02 。
小结
- 对于二元类别变量,计算总体均值和标准差没有意义。取而代之的是,我们计算分类变量的比例。对于二元变量,我们只有总体的比例 $ \pi $ 。
- 相似的逻辑也适用于样本。我们也只有样本比例 p 。对于样本比例的抽样分布来说,我们的确有均值和标准差。只要知道总体的比例,抽样分布的这些参数也很容易计算出来。

