欢迎关注微信公众号「Swift 花园」
分步计划
比较以下两种期望。一,你期望超过半数的持证美国潜水者有超过 35 小时的潜水经验。二,所有持证美国潜水者的平均潜水时长超过 35 小时。第一眼,两个期望看起来很相似。但是,在第一个例子中,你面对的是比例,你感兴趣的是潜水经验超过 35 小时的潜水者的比例。而第二个例子中,你关心的是均值。你想知道潜水时长的均值。因此,当实施显著性检验时,你需要特别注意你的方法。
这一节中,我将以分布计划的方式来引导你。想象你问了一个容量是 500 个持证潜水者的简单随机样本,他们的潜水时长是多少个小时。假设你发现 0.57 的比例有超过 35 小时的潜水经验,时长均值是 35.5 小时,均值是 8 小时。在我们的样本中,
潜水经验的变量分布近似正态。下面是分布计划全图:
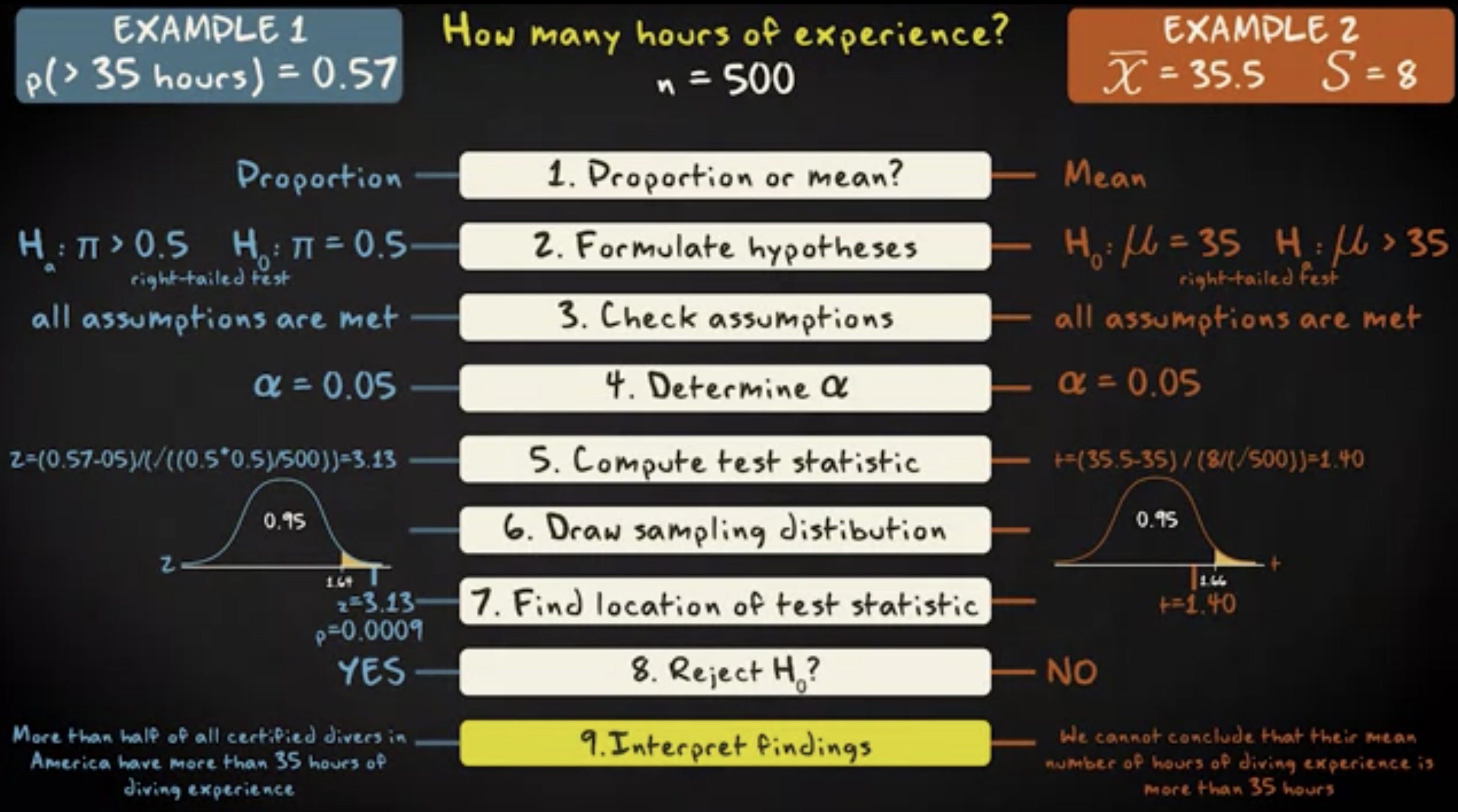
第一步,评估你面对的是比例还是均值,这个我们已经讨论过。第一个例子是比例,第二个例子是均值。
第二步,形式化你的假设。在比例的例子中,零假设是:$ \pi = \pi_0 $ ,在均值的例子中,零假设是 $ \mu = \mu_0 $ 。我们可以有三种类型的备选假设:如果你做双尾检验,是 $ \pi\neq\pi_0 $ 或者 $ \mu\neq\mu_0 $ ;如果你做单尾的右尾检验,是 $ \pi\geq\pi_0 $ 或者 $ \mu\geq\mu_0 $ ;如果你做单尾的左尾检验,是 $ \pi\leq\pi_0 $ ,$ \mu\leq\mu_0 $ 。我们零假设是: $ \pi=0.5,\mu=35 $ ,备选假设是 $ \pi\geq0.5,\mu\geq35 $ 。因此我们需要实施右尾检验。
第三步,检查你的假定是否满足。在两个例子中,随机化都是必要的。你的样本必须通过随机抽样的方法收集,或者说,随机化的实验。在比例的例子中,根据零假设的比例,样本容量乘以比例以及 1 减去样本容量再乘以比例,必须等于或者大于 15 。均值的例子则要求总体分布近似正态。但实践中,这一点只有样本容量很小,且做的是单尾检验时才重要。对于我们的例子,所有的假定都满足。
第四步,确定显著性水平 $ \alpha $ 。常用的显著性水平是 0.05 。我们的检验将基于 $ \alpha=0.05 $ 。
第五步,计算检验统计量。在比例的例子中,公式是 $ z = \frac {p-\pi_0}{se_0} , se_0 = \sqrt {\frac {\pi_0 (1-\pi_0)}{n}} $ ,在均值的例子中,公式是 $ t = \frac {\bar x-\mu_0}{se_0} , se_0 = \frac {s}{n} $ 。注意,在比例的案例中,我们使用 z 分布,而在均值的案例中,我们使用 t 分布。
第六步,抽取相关的抽样分布,展示零假设和检验统计量,补上拒绝域和对应的临界值。在比例的案例中,
第七步,评估你的检验统计量是否落在拒绝域内。
第八步,决定是否拒绝零假设。
第九步,解释你的发现。
在下结论之前,值得提醒的是,不拒绝零值假设并不暗含你就可以接受零值假设。在第二个例子中,我们不拒绝零值假设,即潜水时长等于 35 小时的假设,但并不能得出潜水时长就等于 35 小时的结论。
显著性检验和置信区间
假设你问样本容量为 500 的水肺潜水者他们潜水了多少个小时,均值是 36 小时,标准差是 8 小时,变量的样本分布近似于正态。基于样本信息,你希望推断总体的参数 $ \mu $ ,这是我们所知的推断统计学 —— 基于样本信息得出样本所在总体的结论。
推断统计学有两种方法。其一,通过均值的置信区间来推断区间估计。其二,用显著性检验来推断点估计。在这一节中,我将向你展示这两种方法其实关联密切。

假定你预期潜水时长的均值不是 35 小时,你将做一个显著性检验。我们对均值感兴趣,检验统计量如下:

零假设是: $ \mu = 35 $ ,备选假设是: $ \mu \neq 35 $ 。我们的假定满足,分析基于简单随机样本并且样本足够大,并且样本近似正态分布。检验统计量等于 36 减去 35 ,除以 8 除以 500 的平方根,等于 2.80 。抽样分布看起来是这样的。
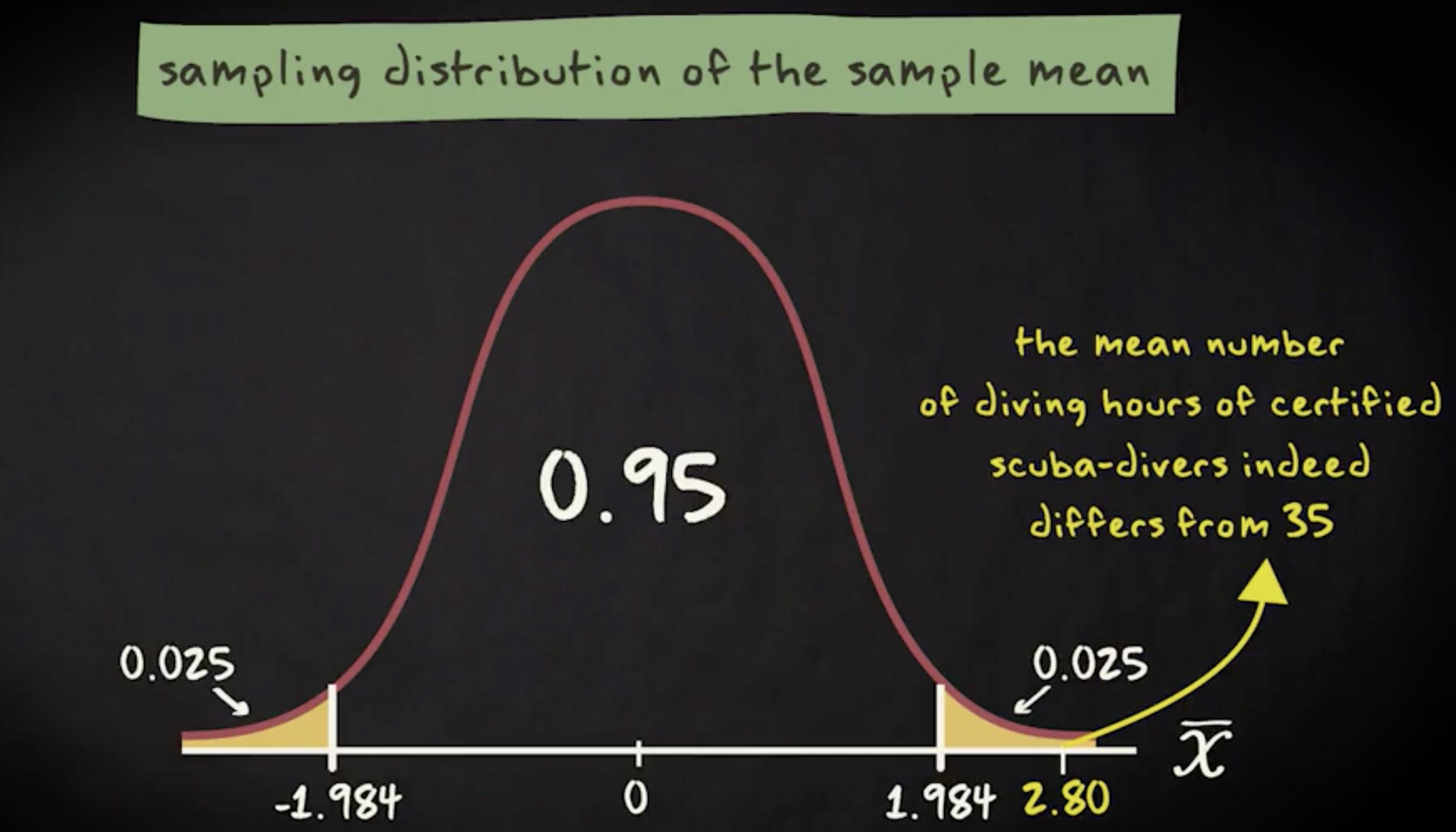
我们可以通过查询 t 表找到对应双尾检验显著性水平 0.05 的临界点是 $ \pm1.984 $ 。因此我们的检验统计量落在拒绝域内。我们将拒绝零假设,得出潜水时长不等于 35 小时的结论。
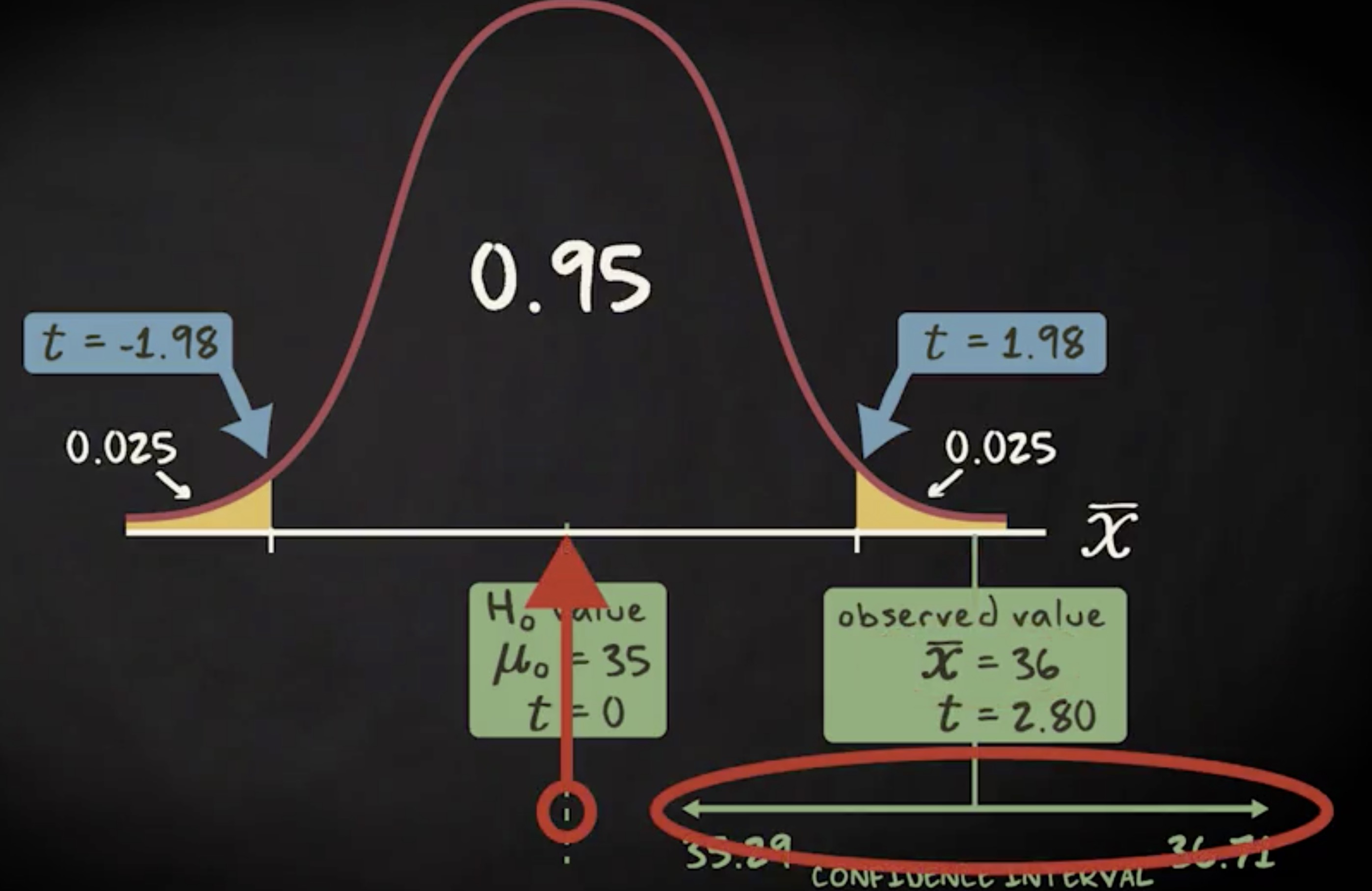
现在,如果我们构造 95% 的置信区间,会发生什么呢?公式如下:样本均值,加减 95% 置信水平对应的 t 分数,乘以标准误差,这个标准误差等于标准差除以样本容量的平方根。相关的 t 分数是 1.984 ,代入公式,得到置信区间是 35.29 到 36.71 。由此我们有信心说,通过无限重复的抽样, 95% 的情况下区间会包含实际的总体均值。这个区间给了我们关于总体均值的一个有说服力的范围。和显著性测试一样,这个置信区间也告诉我们,总体的样本均值不是 35 。通常,双尾显著性检验的结果与置信区间的结果是一致的。

更准确的说,如果双尾显著性检验的 P 值等于或者小于 0.05 ,那么 95% 置信区间也不包含零假设的值。类似的,如果双尾检验的 P 值大于 0.05 ,那么 95% 置信区间将包含零假设的值。

这听起来很合理,对吧?它以下图表示。你会看到,观察值 36 落在拒绝域内,而对应的置信区间也不包含零假设的总体均值。
现在假设观察到的均值是 35.5 ,而不是 36 ,这样的话,我们的检验统计量将变成 1.40 ,它不落在拒绝域内。我们因此不拒绝零假设,相似的,置信区间的两个端点编程 34.79 和 36.21 ,则包含了零假设的均值 35 。
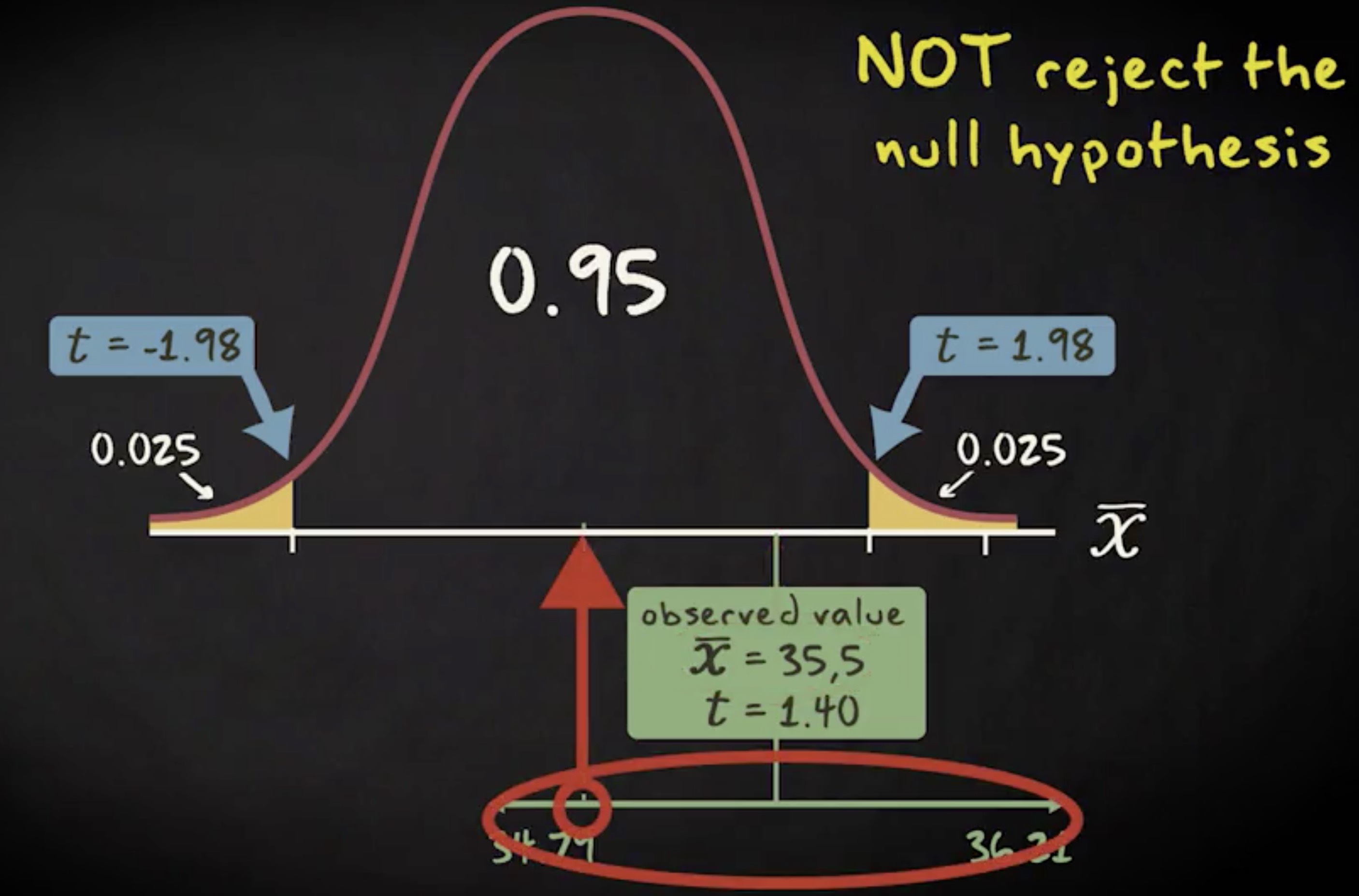
我们可以有信息说,通过无限重复抽样, 95% 的情况区间会包含实际的总体均值。这意味着零假设有说服力,我们不该拒绝零假设。也说明了,构建置信区间的方法和双尾假设检验的方法虽然看起来不同,但是数学上是相关的,彼此一致。


