欢迎关注微信公众号「Swift 花园」
第一类错误和第二类错误
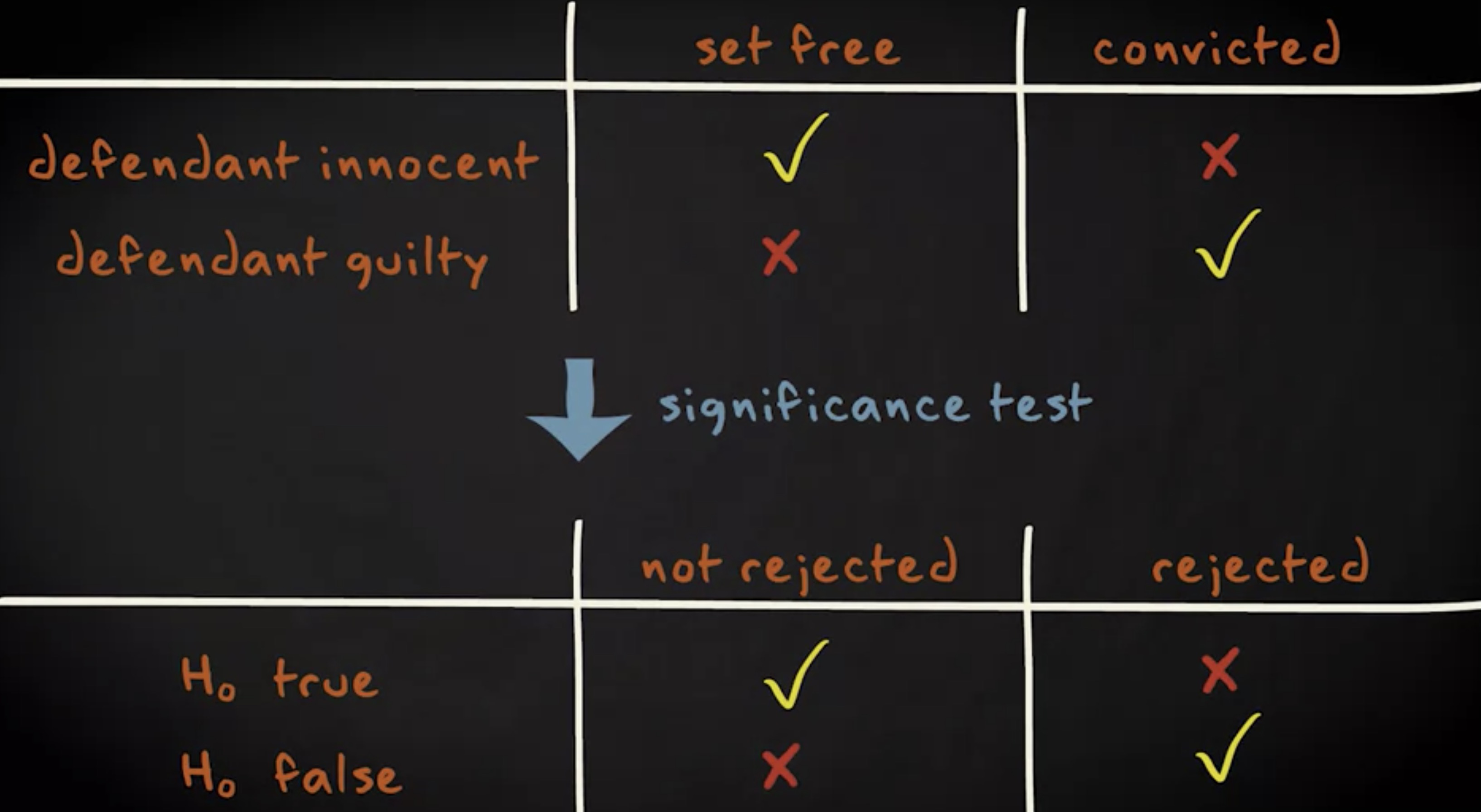
回忆一下此前提到过的庭审的例子。被告方的辩护律师的观点是被告是无辜的,公诉方则试图说服陪审团和法官被告是有罪的。举证有罪的责任在于原告。被告只有在原告提供有力证据驳斥被告假定无罪的情况下才能被认定为有罪。
在审判时,有四种可能的结果。一,被告确实有罪且被判有罪,这是个正确的决定。二,被告确实无辜且被判无罪,这也是正确的决定。三,被告实际上是无辜的,但被判有罪,这是错误的决定。四,被告实际上有罪的,但是被判无罪,这也是错误的决定。
这也是我们在实施显著性检验时会发生的情况。辩方观点类似零假设为真,而被告有罪则等效于零假设为假。判被告有罪类似拒绝零假设,而无罪释放则等同于不拒绝零假设。这会导致四种可能的情形。其中的两种,你做了正确的决定,包括零假设的确为真并且你没有拒绝它以及零假设的确为假并且你拒绝了它。但也有两种你做了错误的决定,包括零假设为真而你拒绝了它以及零假设的确为假而你没有拒绝它。第一个错误我们称为 第一类错误 (type I error) ,或者说 伪阳性 (false positive) 。第个错误我们称为 第二类错误 (type II error) ,或者说 伪阴性 (false negative) 。
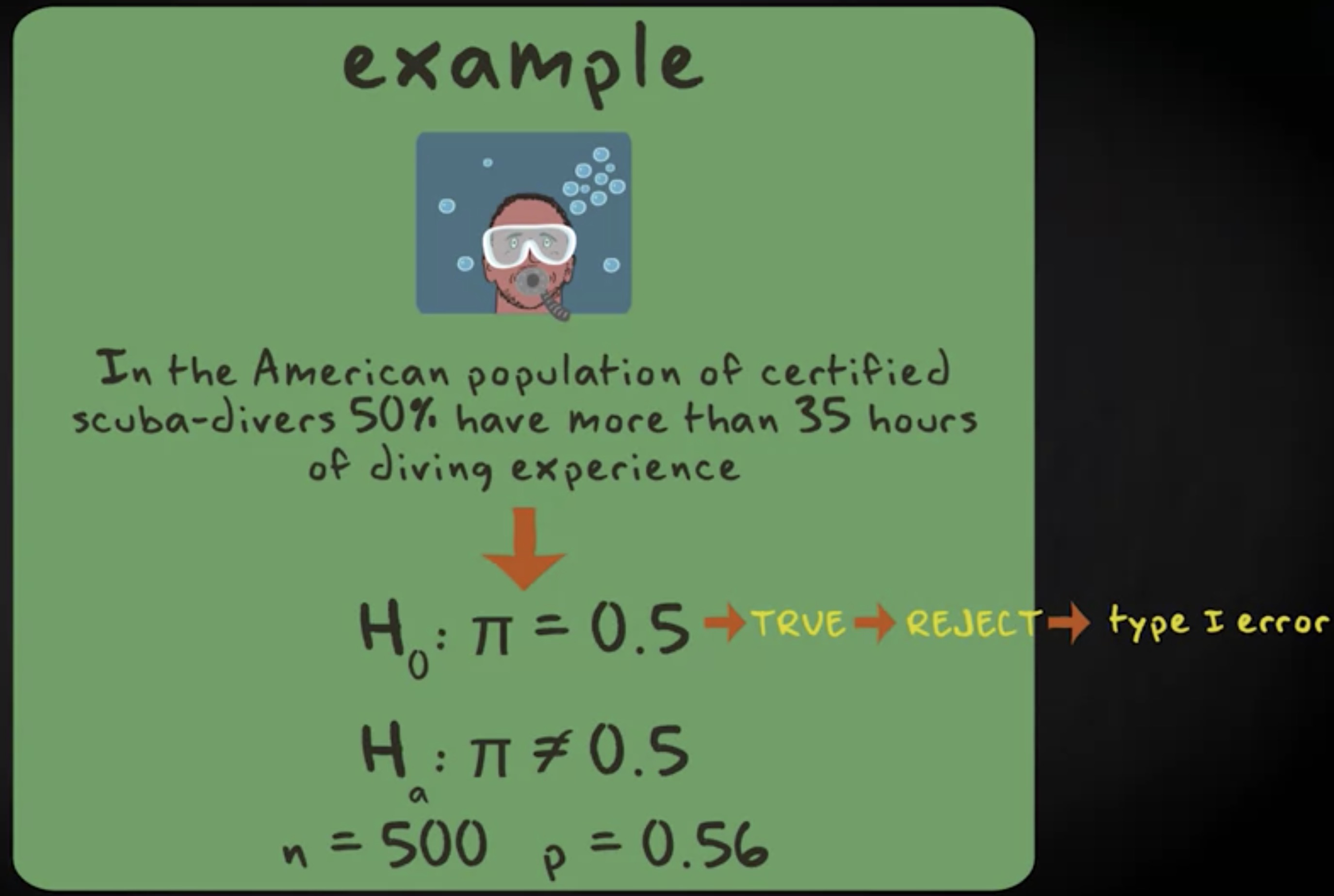
让我给你举个例子。想象你的零假设是:美国的持证水肺潜水者总体, 50% 有超过 35 小时的潜水经验。换言之, $ \pi = 0.5 $ 。备选假设是它是另外一个百分比,换言之, $ \pi \neq 0.5 $ 。你问了一组简单随机抽样的 500 个美国潜水者,你发现有 0.56 的比例有超过 35 小时的潜水经验。现在,假定你的零假设实际上是真的,当你决定基于你的样本数据拒绝零假设时,一个第一类错误就出现了。
如果零假设为真,抽样分布是像下面这样的:
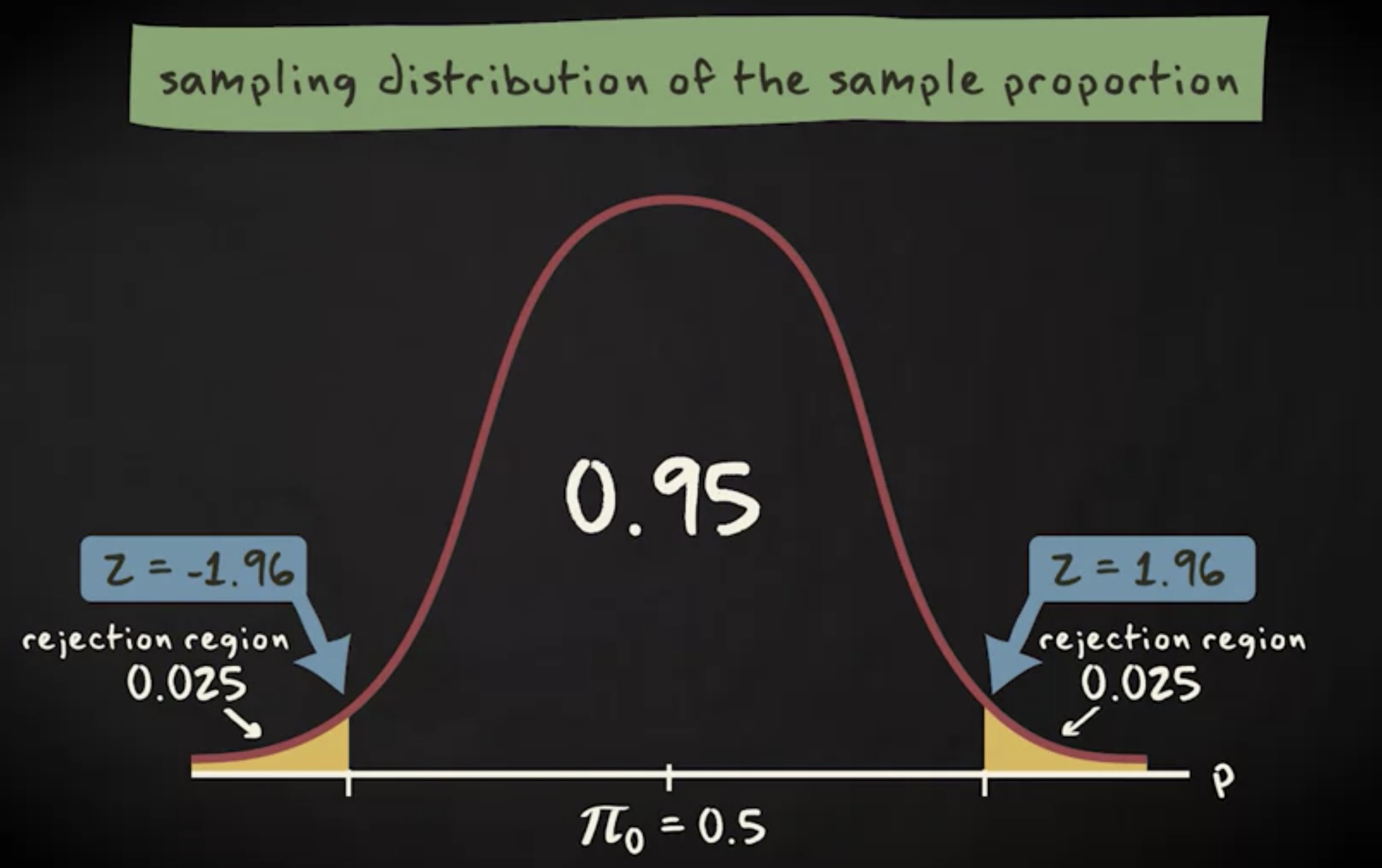
如果你的显著性水平 $ \alpha $ 等于 0.05 ,通过查询 z 表得到临界值是 -1.96 和 1.96 。你的检验统计量落在拒绝域内。换言之,你要拒绝零假设。这件事情发生的概率是 0.025 加上 0.025 ,等于 0.05 。意味着第一类错误发生的概率等于显著性水平。
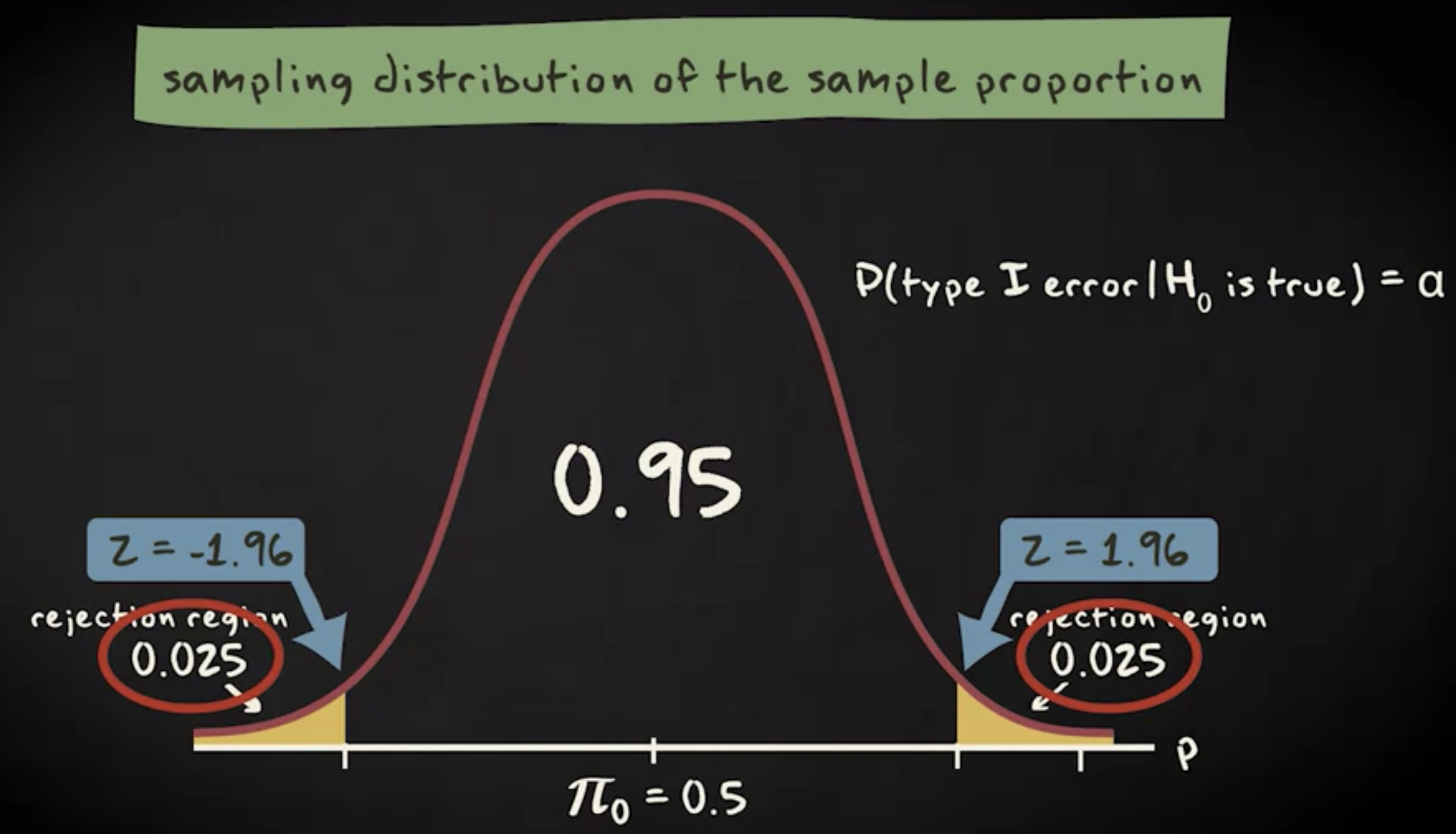
由此,你可能想到要降低显著性水平。
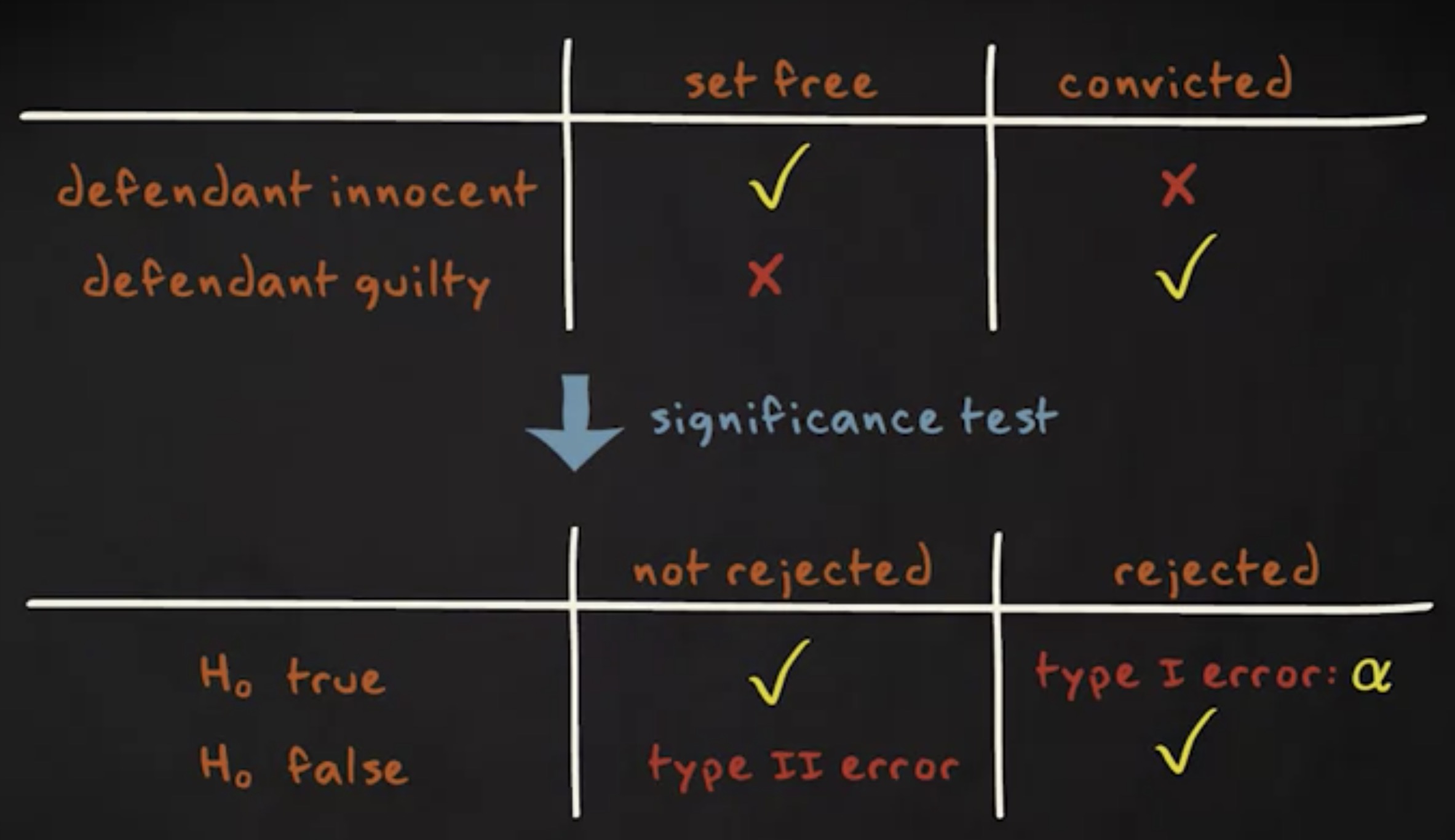
但是,这不一定是个好主意。如果你在零假设实际为真时降低了错误地拒绝它的概率,你实际上增加了零假设实际为假而你错误地没有拒绝它的概率。

犯第二类错误的概率我们称为 $ \beta $ 。
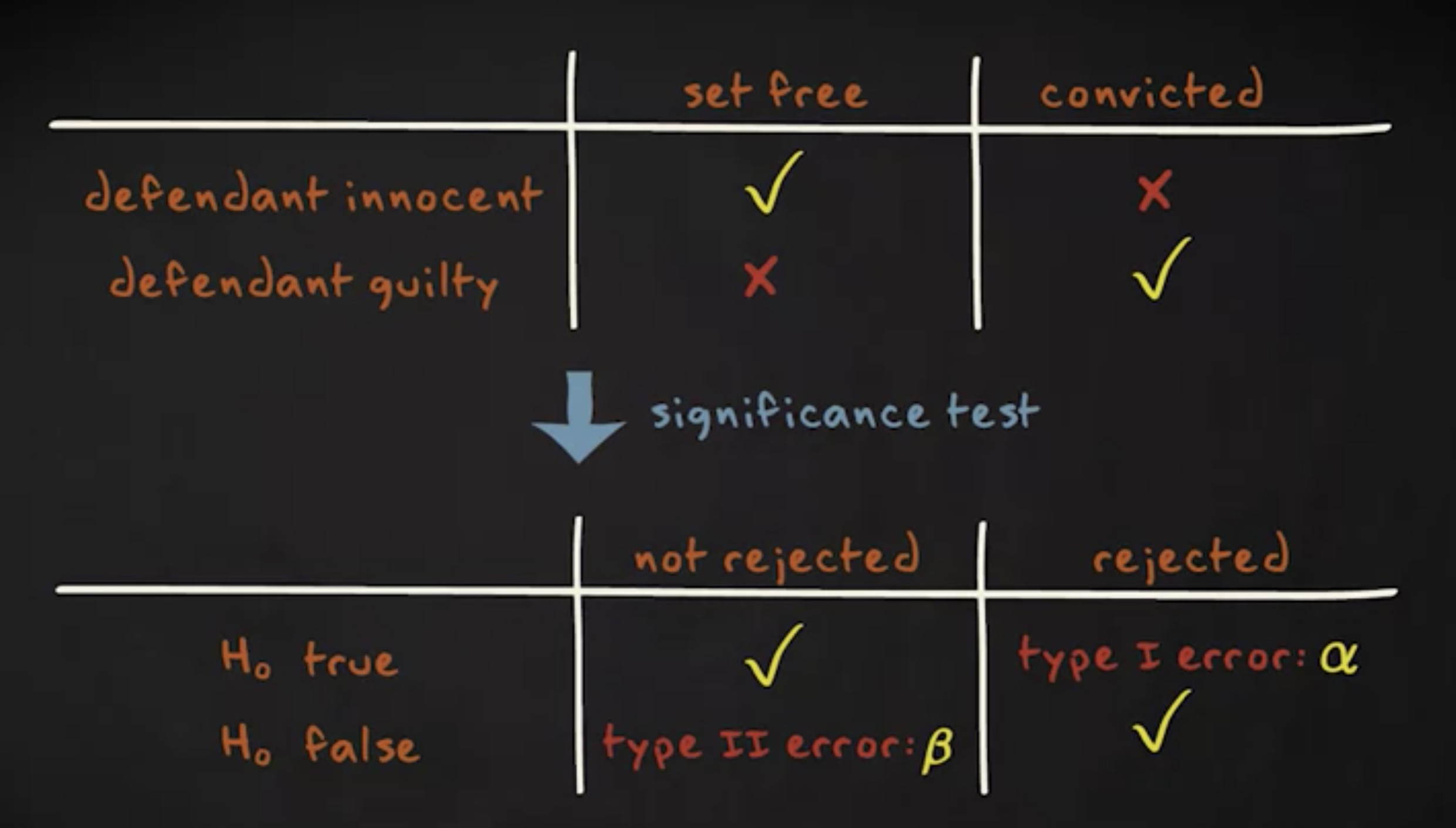
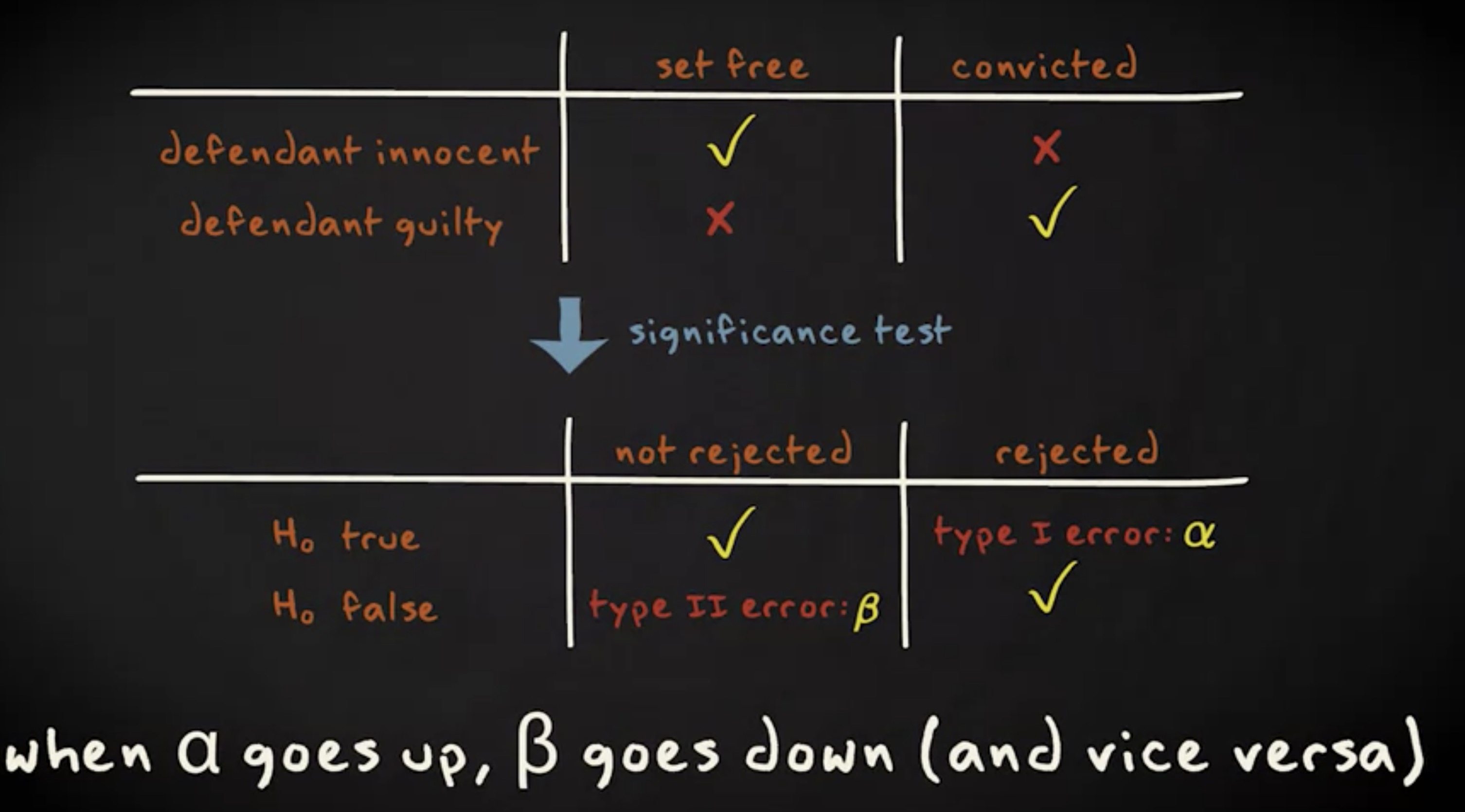
计算 $ \beta $ 相当复杂,它依赖各种因素,例如 $ \alpha $ 的值,样本容量以及参数的真实值。基于这个原因,我们并不会去计算 $ \beta $ 的值,但重要的是你需要意识到,当我们试图降低某一类错误的概率时,另一类错误的概率会上升。
当零假设为假时,并且你实施了检验,你希望检验的 功效 (power) 是高的。检验的功效是拒绝零假设的概率,给定它为假,换言之,一个检验的功效等于 1 减去第二类错误的概率,也就是 $ 1 - \beta $ 。
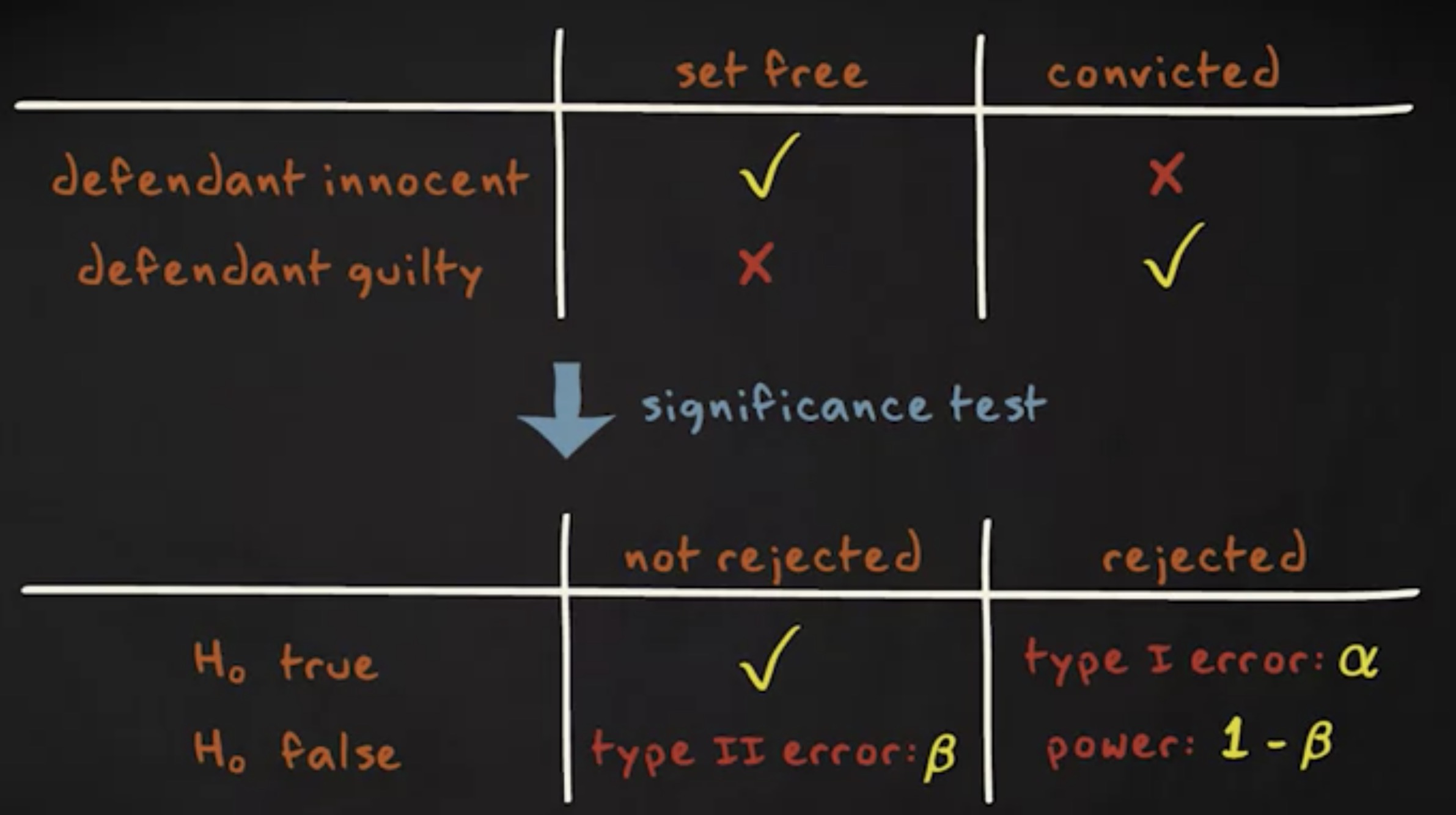
为什么功效这么重要呢?是这样的,当你要实施一项研究之前,它可以帮助你确定你需要多少的参与者。在你实施完研究之后,它能帮助你确定结论不是统计显著的。
最后一个提示,在实践中,你永远无从得知某个决定正确与否。我们唯一能做的是控制做出不正确决定的概率。
例子
想象你是一个对鲸鲨感兴趣的潜水者,你想要知道这些巨大的动物平均的身长有多少。我们还假设你已经花费了很多年在世界各地研究了这些生物。这些年你已经测量了 258 头鲸鲨。因为你已经测量了世界各地的鲸鲨,我们假定这 258 头鲸鲨可以被看作一个简单随机样本。平均的长度等于 8.3 米,样本标准差是 3.4 米,并且鲸鲨长度的分布也近似正态分布。

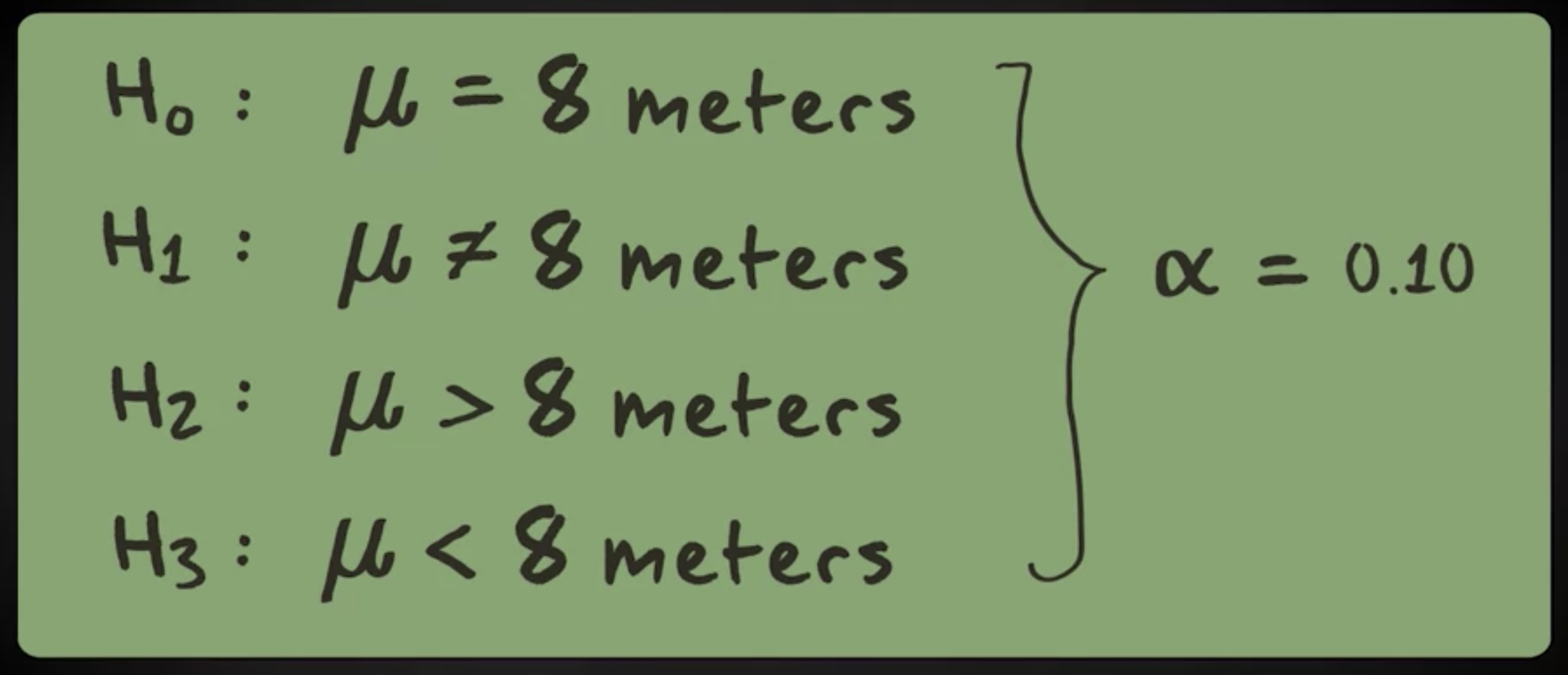
在这一节中,我们将检验三种备选假设和一种零假设:鲸鲨总体的长度均值等于 8 米。第一个假设是总体均值不是 8 米。第二个假设是均值大于 8 米,第三个假设是总体均值小于 8 米。所有这几种情况中,我们都把显著性水平设为 0.10 。
首先,我们得检查我们的假定。如我之前说过的,鲸鲨的选择可以看作是简单随机抽样,并且我们也看到鲸鲨身长的分布近似正态。因此,我们没有理由预期总体分布会和正态分布差异巨大。再者,这也不是个问题,因为我们的样本量相当大。
现在,让我们计算检验统计量,它的值对于几个假设都是一样的,毕竟,样本均值和零假设一样。

代入公式, 8.3 减去 8 ,除以 3.4 除以 258 的平方根,等于大约 1.42 。
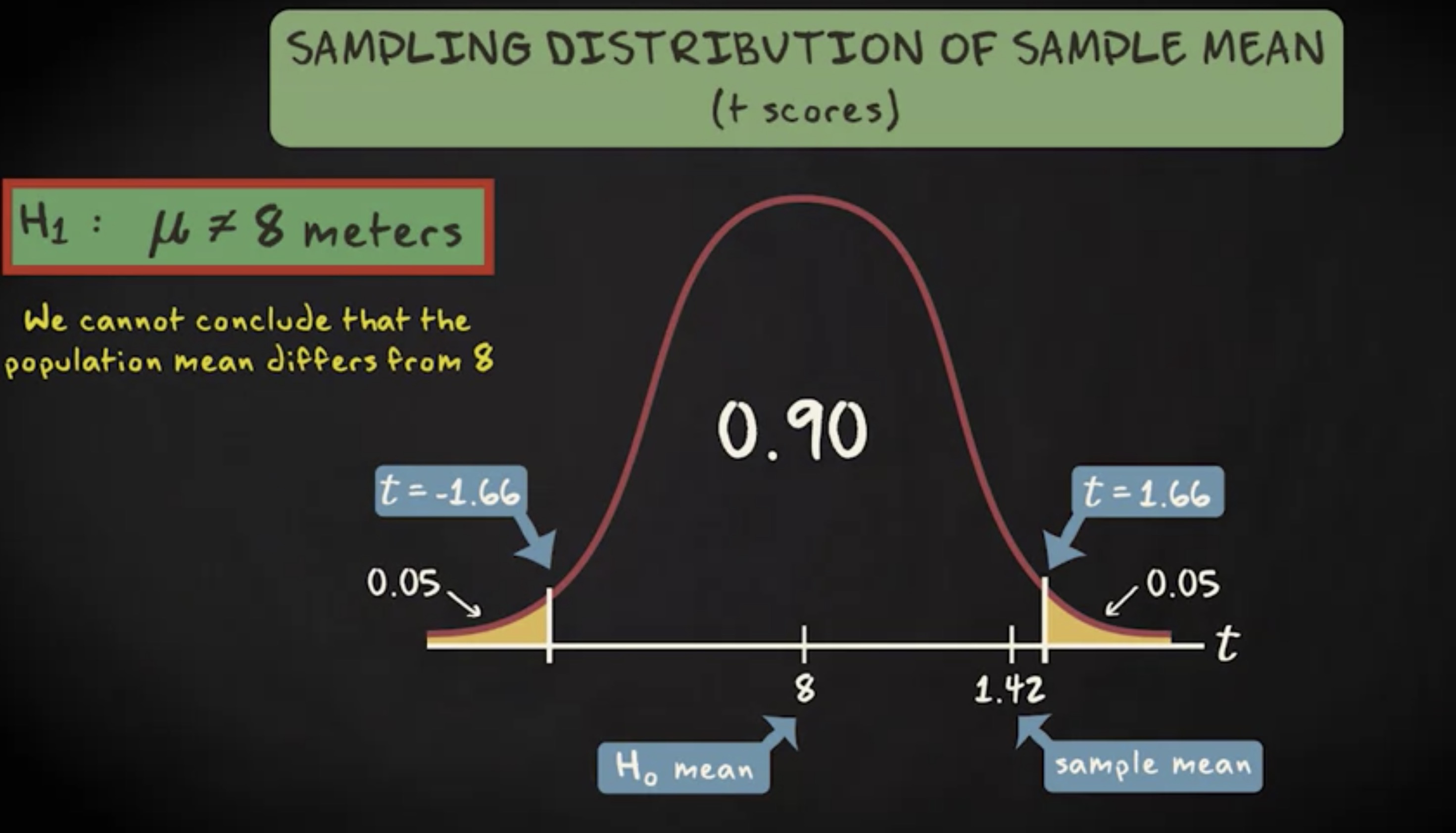
现在,我们开始第一个备选假设,它断言总体均值不是 8 米。我们画出相关的抽样分布,并显示零假设的值。我们需要基于 0.01 的显著性水平做双尾检验,查询 t 表格得到临界值 -1.66 和 1.66 ,检验统计量等于 1.42 不在拒绝域内因为我们不拒绝零假设。这意味着基于 0.10 的显著性水平,我们不能得出总体均值不是 8 的结论。
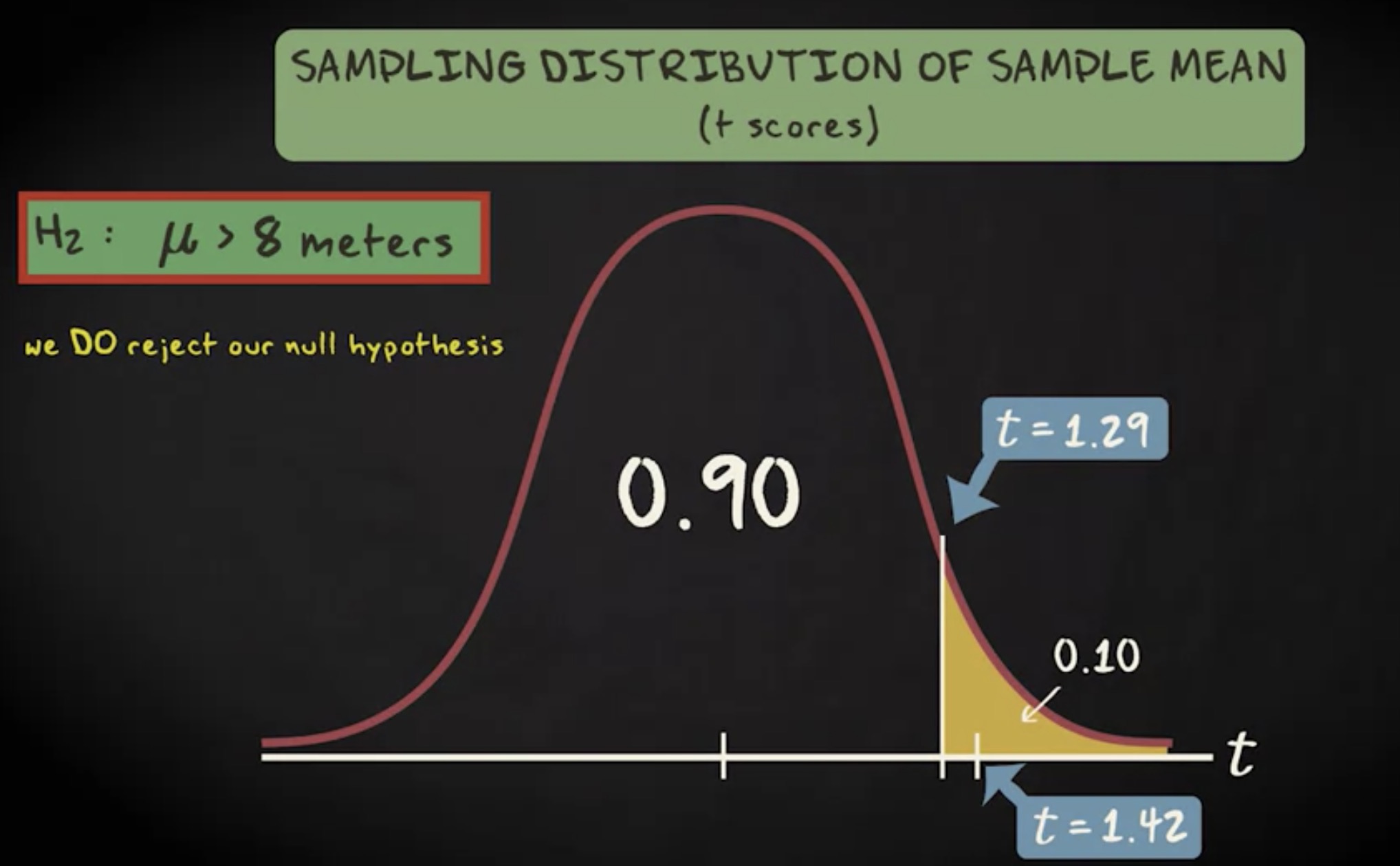
第二个备选假设是总体均值大于 8 。抽样分布一样,但这一次我们做右尾检验。查询 t 表格得临界值是 1.29 ,这一次检验统计量是落在拒绝域内。因此在这种情况下,我们拒绝零假设,并且下结论总体的均值的确大于 8 。
最后的备选假设是总体均值小于 8 。在这种情况下,我们做左尾检验,它是右尾的镜像,所以相关的临界值是 -1.29 。现在我们的检验统计量是 1.42 ,对于临界值时一个极端值,但它在分布的另一边。这意味着,它也不在拒绝域内,因此我们也不拒绝零假设。
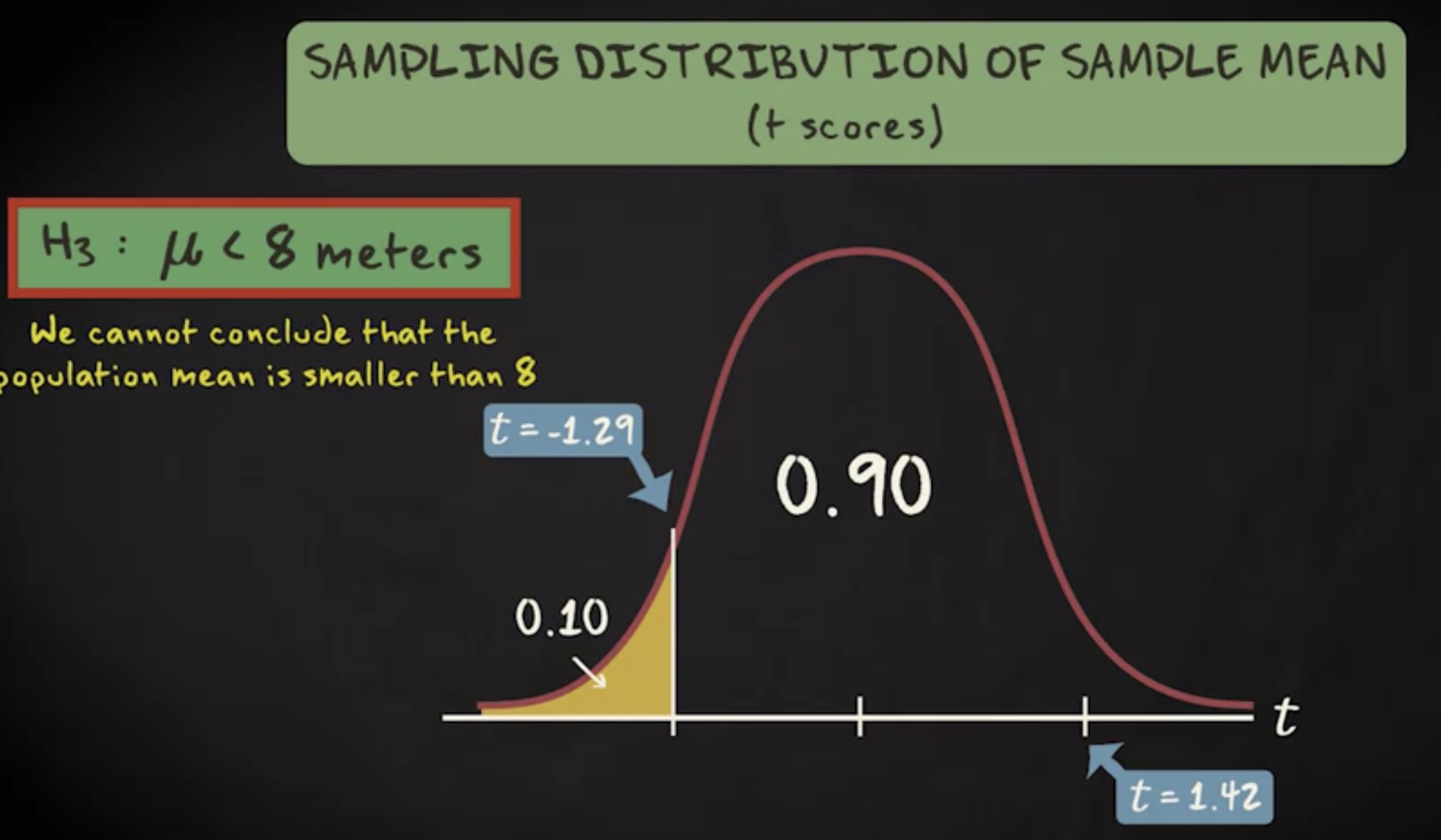
最后的例子显示,画出抽样分布很重要。否则,你可能会无法注意到检验统计量相对于临界值处于分布的另一边。不论检验的结果如何,有两件事是可以确定的。第一,鲸鲨真的很大。第二,教程即将结束,我要放假啦~感谢阅读!

