欢迎关注微信公众号「Swift 花园」
通俗解释 z-score ,即 z-score 是对某一原始分值进行转换,变成的一个标准分值,该标准分值可使得原来无法比较的数值变得可比。
Z-score
本教程中我们还继续沿用前面教程中足球队的例子。

你在这里看到的是所谓的球员纹身占比,以纹身占身体的百分比表示。点图和标准差表明,第二队的分布比第一队的变化更大。
有时研究人员会问:一个特定的观测结果是常见还是特例。为了回答这个问题,研究人员会用 一个数与平均数的差再除以标准差 。这个数字就是我们所说的 z 分数。在这篇教程中,我将解释如何计算 z 分数,以及它们的用处。
我们先来看看第一队的分布情况。平均数是 15 ,标准差是 2.5 。为了计算 z 分数,我们使用这个公式:
这个公式不是很复杂,它告诉你如何计算感兴趣的数值。该数值与平均数之差,再除以标准差。
来看看纹身占比是 10.8% 意味着什么。该值的 z 分数是 10.8 减去 15 再除以 2.5 等于负 1.68 。所以 z 分数是负 1.68 。你可以为所有数值进行如此计算。如果这样做,这些就是结果。

请注意,最终会得到负 z 分数和正 z 分数。负 z 分数表示低于平均数的值;正 z 分数表示高于平均数的值。因为平均数是分布的平衡点,所以负的和正的 z 分数相互抵消。换句话说,如果将所有 z 分数相加,结果为 0 。
好的,不过如何知道某个 z 分数是低还是高呢?
这取决于分布和前后关系。有一个黄金定律:如果变量的直方图是钟形的,那么 68% 的观测值在 z 分数 -1 和 1 之间, 95% 在 z 分数 -2 和 2 之间, 99% 在 z 分数 -3 和 3 之间。这意味着对于这种类型的分布, z 分数大于 3 或小于 -3 ,可以被认定是特例。
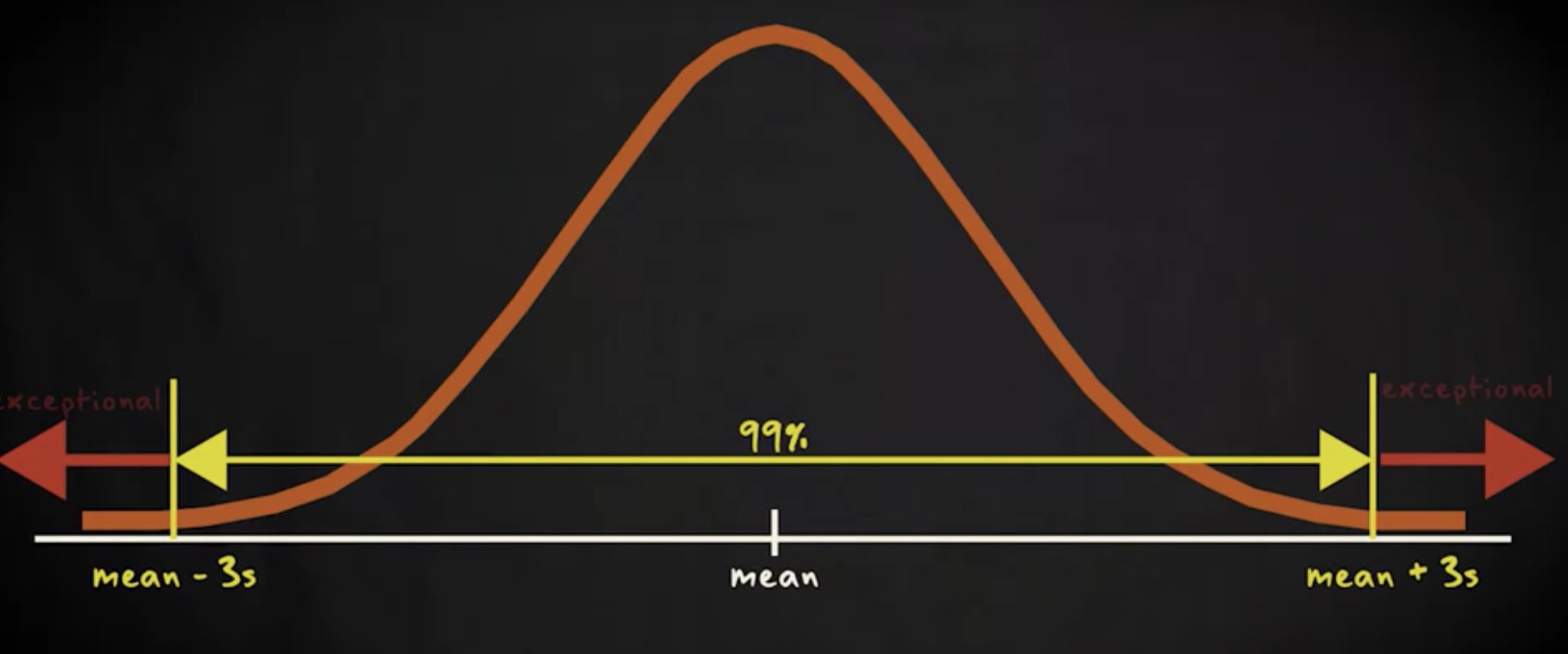
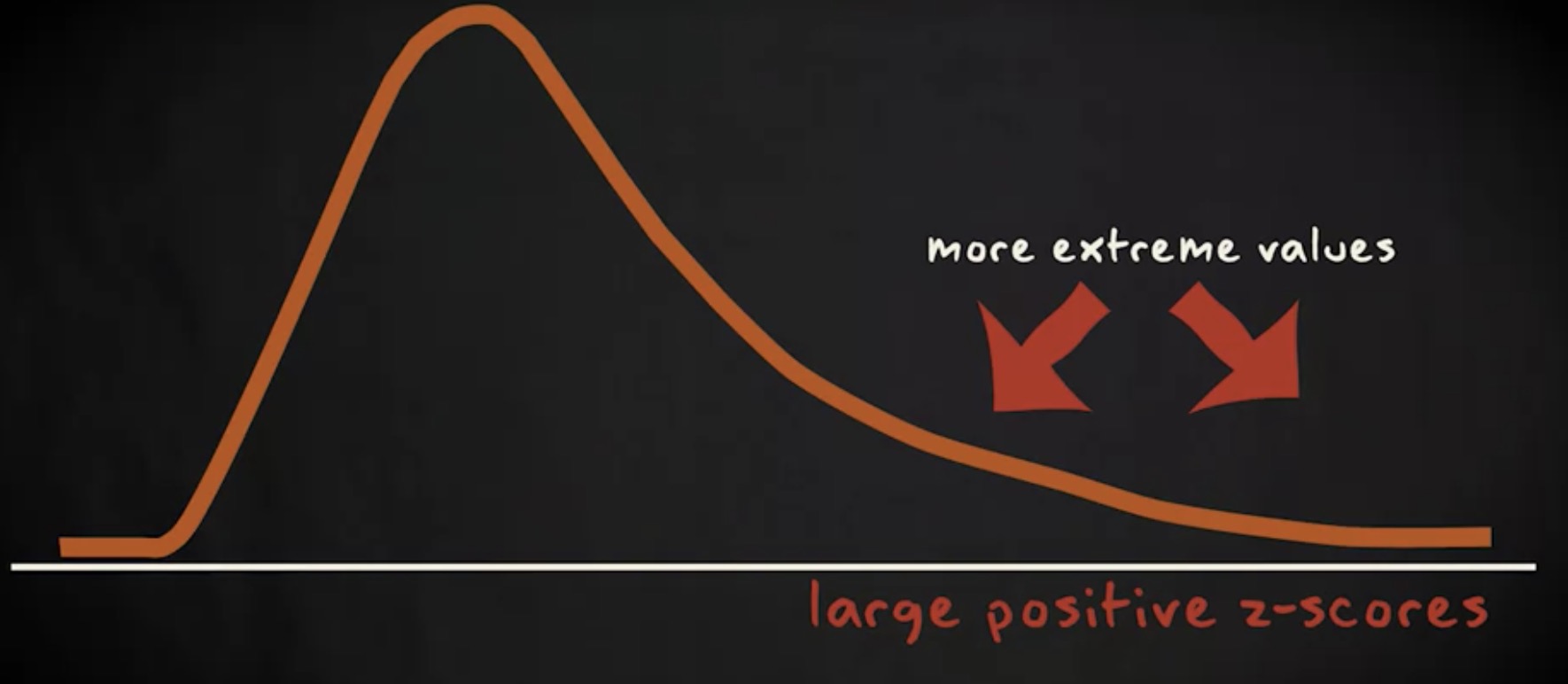
但是,如果分布严重偏向右侧,如下图所示,较大的正 z 分数会更常见,因为分布的右侧有更多极值。
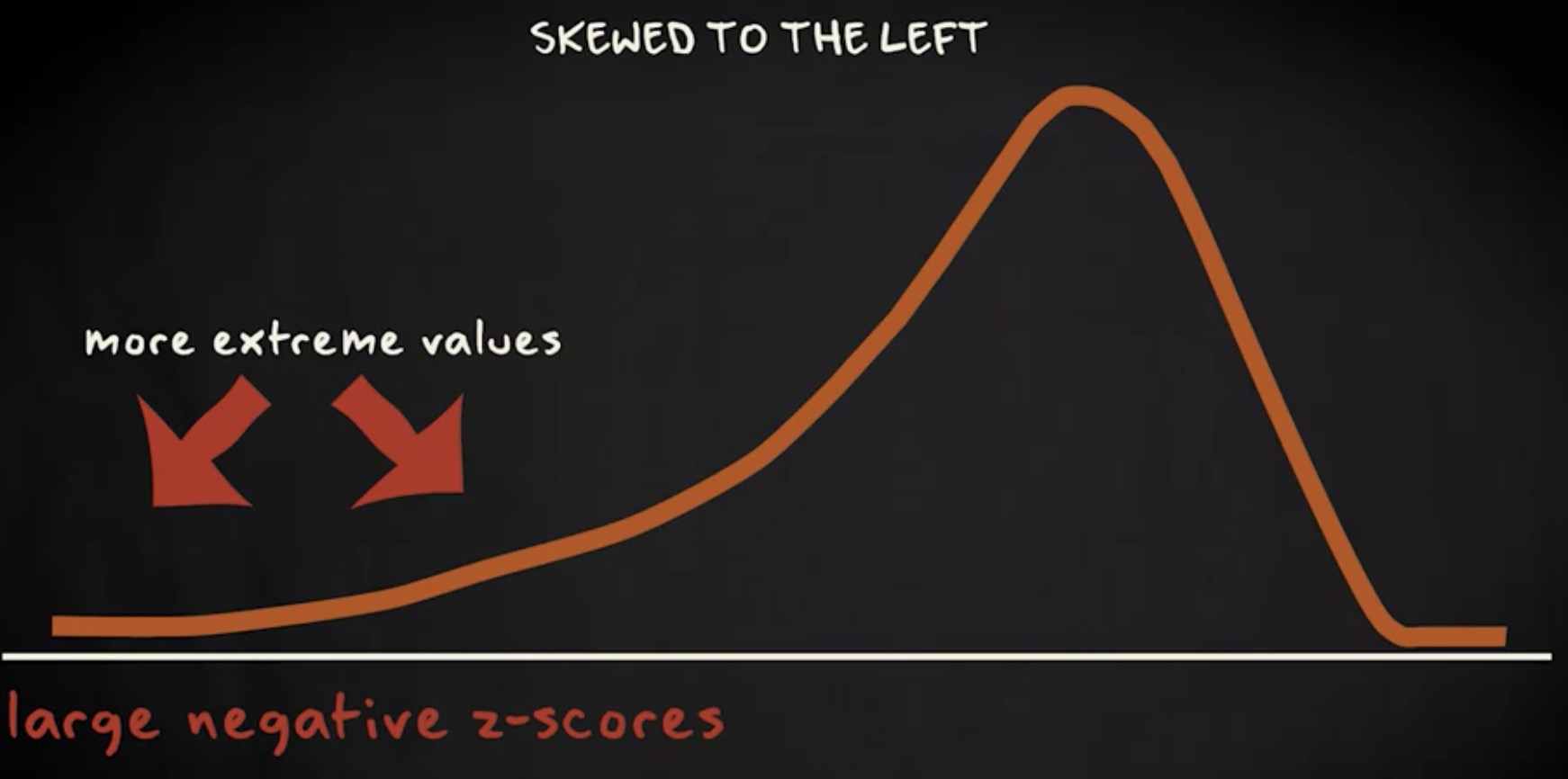
类似,如果分布严重偏向左侧 则较大的负 z 分数会更常见,因为分布的左侧存在更多极值。
无须考虑形状,适用于任何分布的规则。 75% 的数据必须落在 z 分数正负 2 之内。
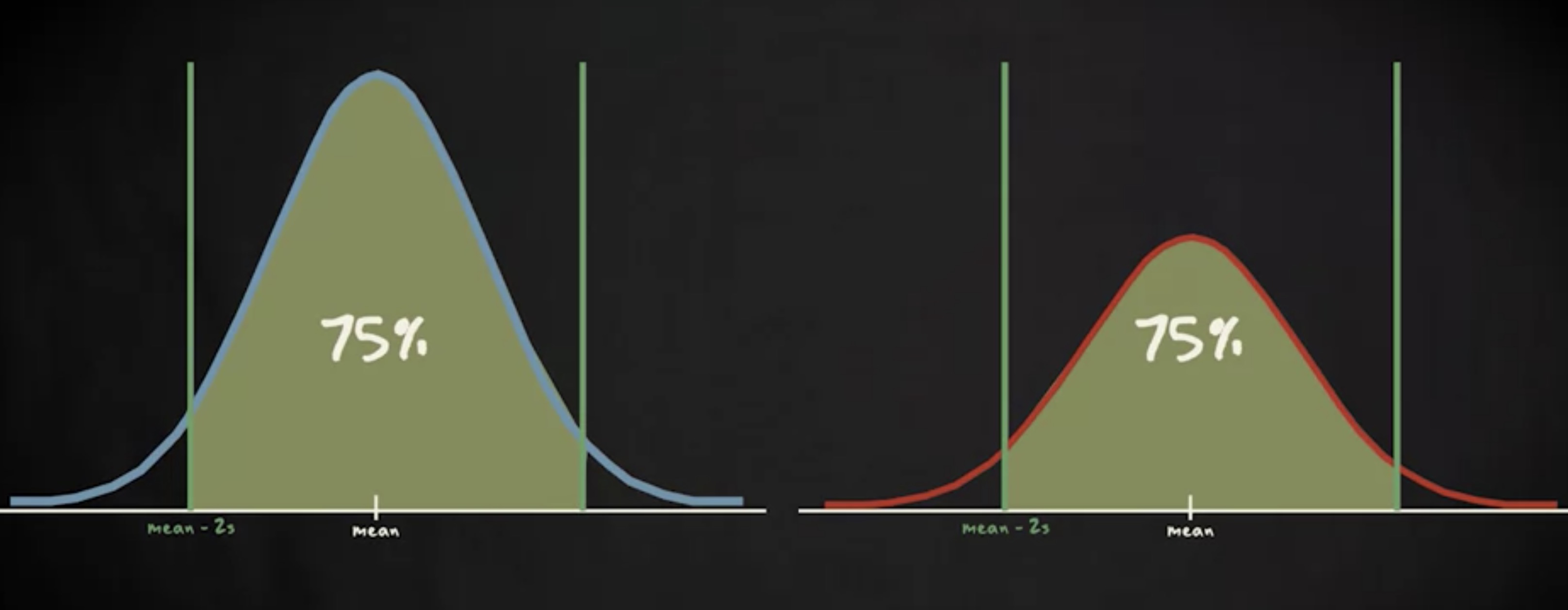
且 89% 的数据在 z 分数正负 3 之间。
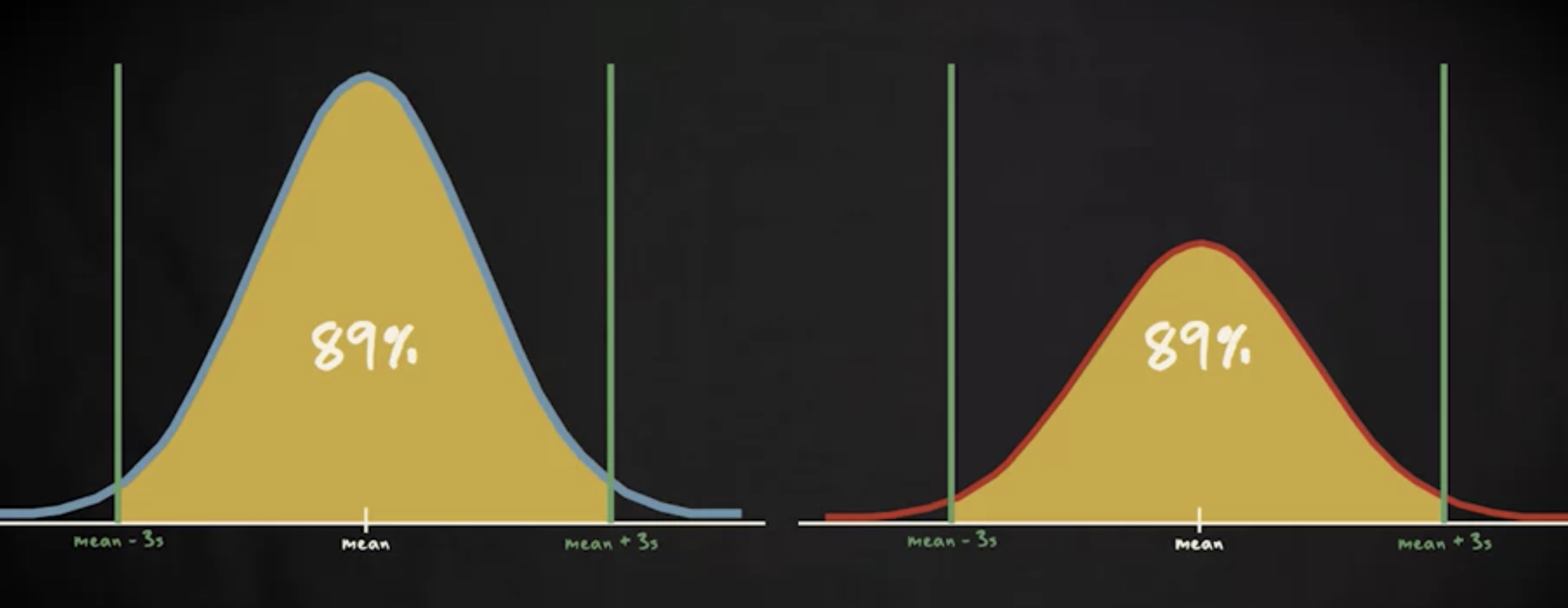
因此, z 分数本身就在一定程度上,给出了关于观测极端程度的信息。如果要比较不同的分布, z 分数就更有用了。比如,来看一下 19.3 的体重是否常见:
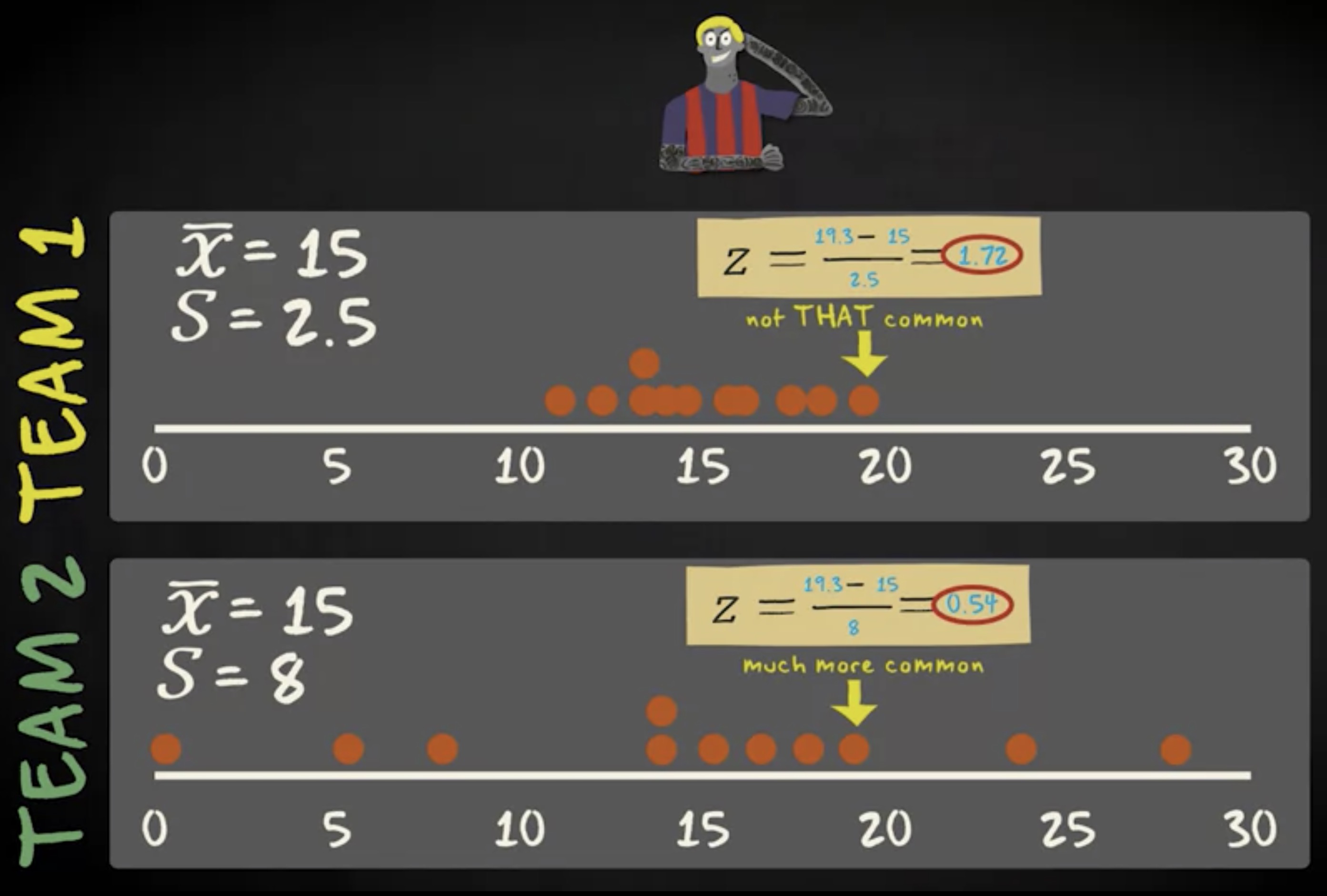
在第 1 组中,这并不常见。 z 分数为 19.3 减去 15 再除以 2.5 ,等于 1.72 。在第 2 组中, 19.3 的 z 分数等于 19.3 减去 15 除以 8 等于 0.54 。这表明在第 2 组中, 19.3 的体重更常见。在第 2 组中, z 分数是 0.54 ,在第 1 组中,是 1.72 。
小结
如果我们将原始分数重新编码为 z 分数,就是 将变量标准化 。 标准化 意味着我们用 z 分数 替换原始度量中测量的分数,其优点是我们可以一眼看出特定分数是相对常见还是特殊。
因此,一个球员纹身占比是五分之一是否异常,这取决于球队或你想比对的另一组数据。

