欢迎关注微信公众号「Swift 花园」
联合概率和边际概率
对有趣现象的计数,在日常生活中常常转换成比例,最终变为概率。利用概率估算的力量,可以更好地理解这些现象之间的关系或做出预测。 联合概率 (joint probability) 和 边际概率 (marginal probability) 是两个在这种情况下会用到的重要概率类型。在这一节教程中,我将解释联合概率和边际概率的含义,并展示它们的属性。
想象你在沙滩上观察你的海滩同伴。你会注意到三种不同类型的活动 —— 它们是互斥的。有的休息,他们都坐在或躺在沙滩上。有的玩,这些人到处乱跑,建造沙堡或站在水中。最后,有的在游泳。此外,你还可以按性别区分。所以你观察到的每个人都是一个案例.

在数据集中,性别和活动是变量。你最终得到以下结果的列联表。总共计了 113 人,其中有 79 人在休息,有 20 人在玩,并且他们中只有 14 人在游泳。女性和男性的数量,分别是 62 和 51 。
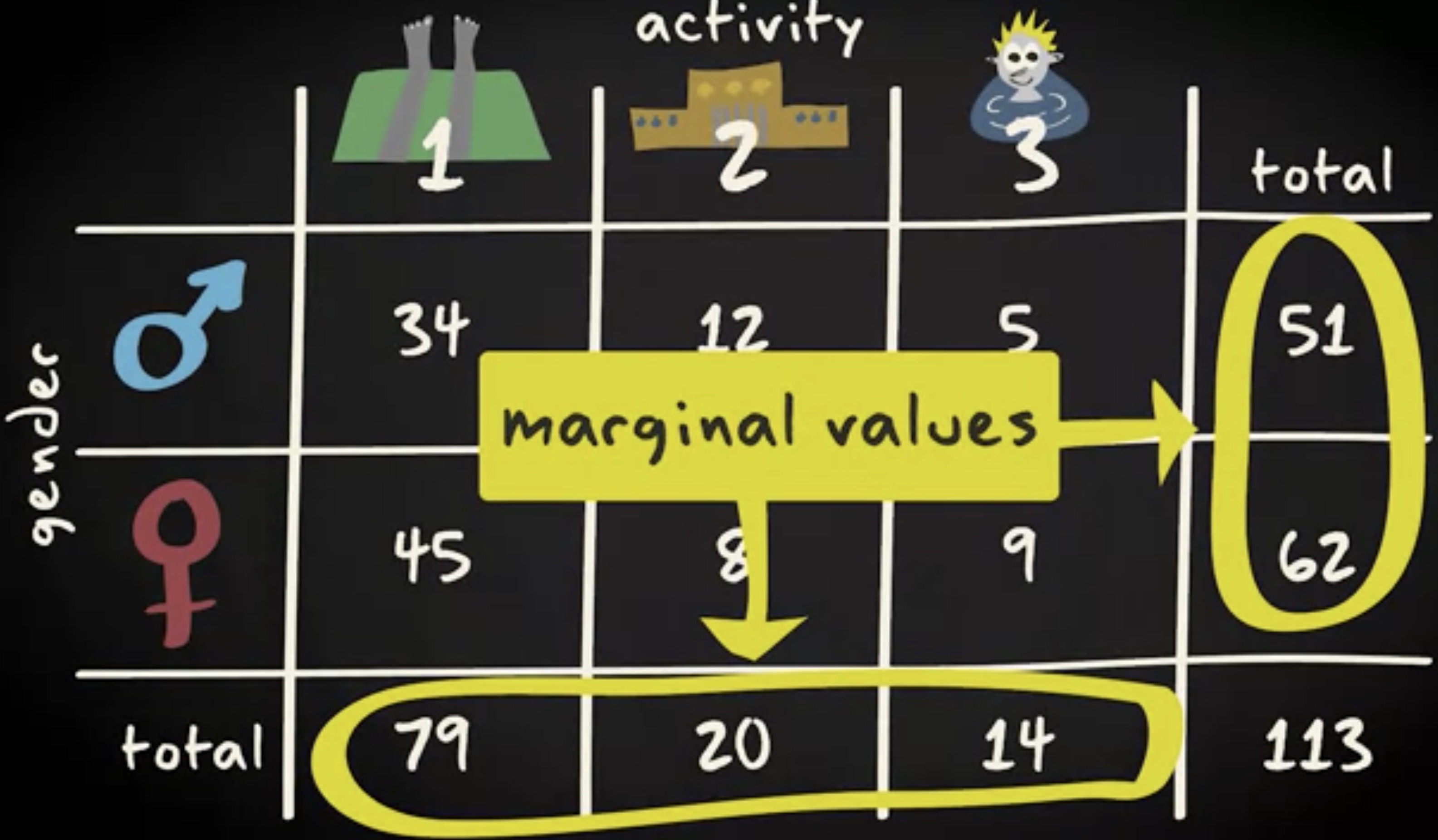
这些数字实际上是每行和每列变量位于此表边缘的总和,因此被称为边际值。请注意,这与口语上 “边缘的”,即并不重要的,并不是一回事。在表中边际值代表对于单个变量的说明,没有关于任何其他变量。例如说休息的人数不考虑性别。
现在,我们打开这个频率表通过将每个单元格数字除以总数 113 得到比例的表格。

在此表中,中心块包含六个位置,它们加起来等于一。同时,每列中的比例加总到底部的边缘行中的值,每行中的比例加总到右边的边缘列中的值。并且边缘行的值加起来等于边缘列的值加起来。
你的计数可以看作随机样本,测量在海滩的人的活动和性别分布,于是你会想到把比例看作概率。在中间区域,是活动与性别的交集。例如,给定的人是男性,正在游泳。这些值称为 联合概率 (conditional probability) 。 联合概率只是各种事件的交集概率的简称 。
我们的每个联合概率关联的事件都与表中任何其他联合概率关联的事件互斥,因为每个人在海滩上只被放置在六个互斥事件之一。同时,联合概率形成一系列完全穷尽的事件,因为案例中不会出现其他的可能活动和性别的组合。因此,联合概率总和为一。
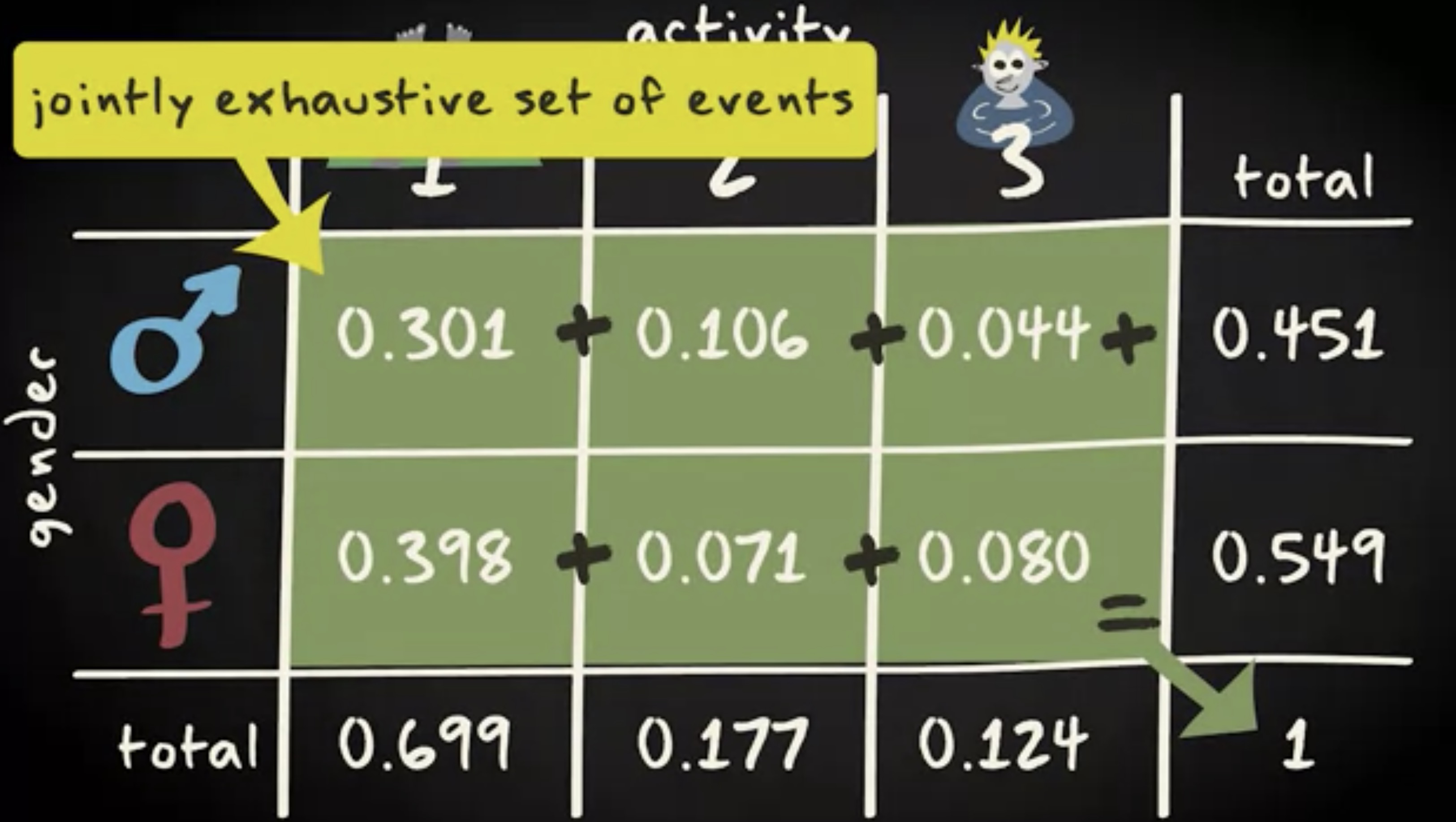
在边缘的地方,你可能期望有 边际概率 。是的,这些概率仅考虑一个变量。例如,给定的人是男性,无论其活动如何,或者给定在玩,不论性别。边际概率来自联合概率的并集。例如休息的概率,玩耍的概率和游泳概率。因此,这里适用加法规则,即概率相加。
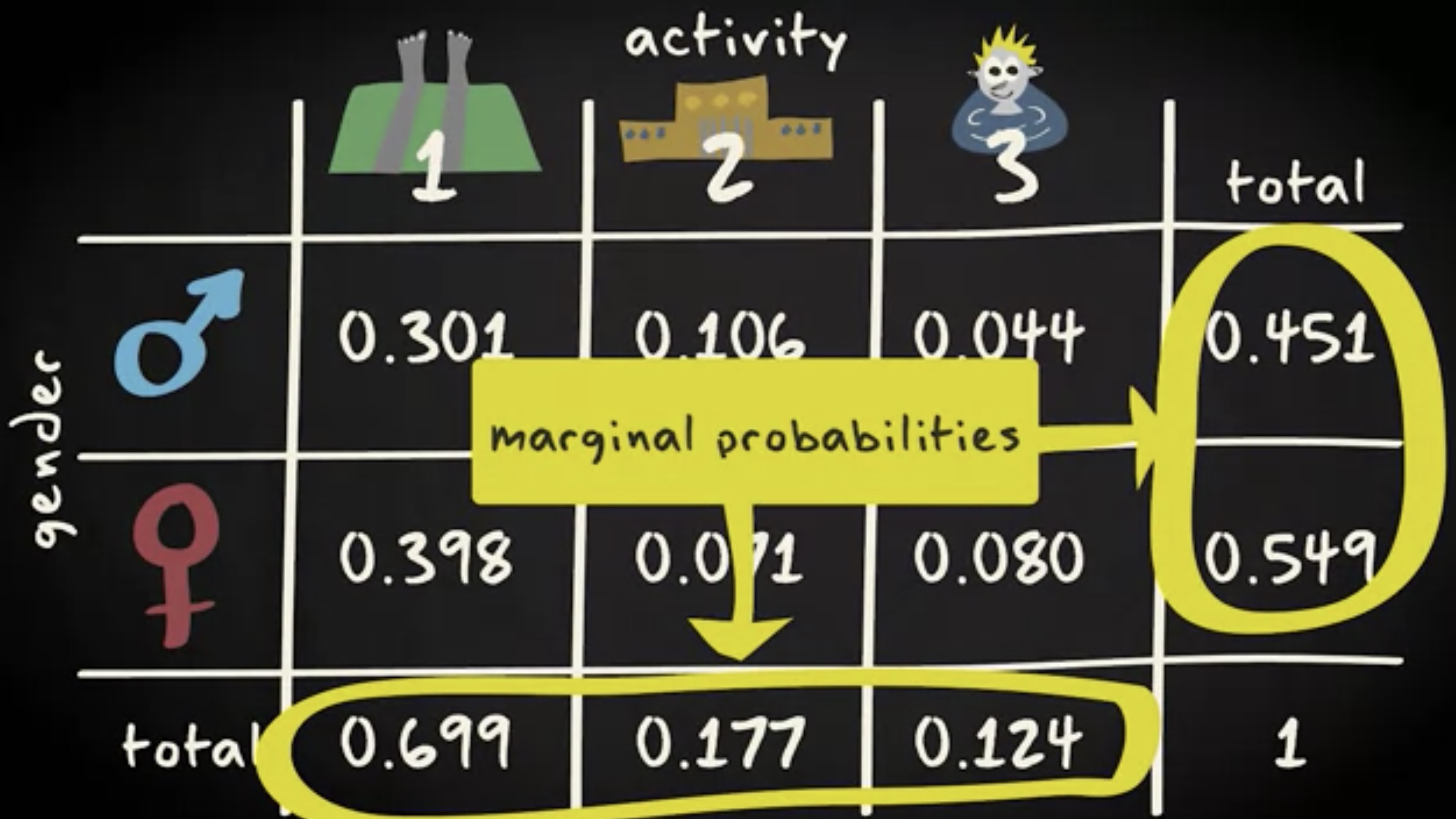
因此,如果你的原始计数不可得,但有联合概率,你始终可以计算出边际概率 —— 通过求和。相反,如果只给你边际概率,你将无法在每种情况下反推出联合概率。
小结
- 当你在对源自一个随机样本或者试验中的现象计数时,可以把它们转换成概率。
- 如果观察多个随机变量,可以计算出这些变量的联合概率和边际概率。
- 联合概率是变量间某些结果交集的概率,而边际概率是每个变量所有结果概率的总和。
- 典型的例子里,如果变量有两个,列联表示组织数据的绝佳形式。联合概率放在中间,边际概率放在边缘。所有的联合概率加起来等于 1 ,它们在两个方向上分布加总得到一个边际概率。
- 你总是可以通过加总,基于联合概率算出边际概率;但仅有边际概率,不借助额外的假定是无法算出联合概率的。
条件概率
术语 条件 (condition) 意味着取决于别的东西。和日常语言中的概率上下文或多或少具有相同的含义。
其正式定义是:给定另外一件事已发生,这件事件发生的可能性。数学符号如下:
即给定 B 发生或以 B 为条件,事件 A 发生。垂直线是 “给定” 的速记,或者说 “有条件” 的速记。条件概率的计算公式是:
即事件 A 和事件 B 都发生的概率除以事件 B 发生的概率。也可以用下面的文氏图来说明:
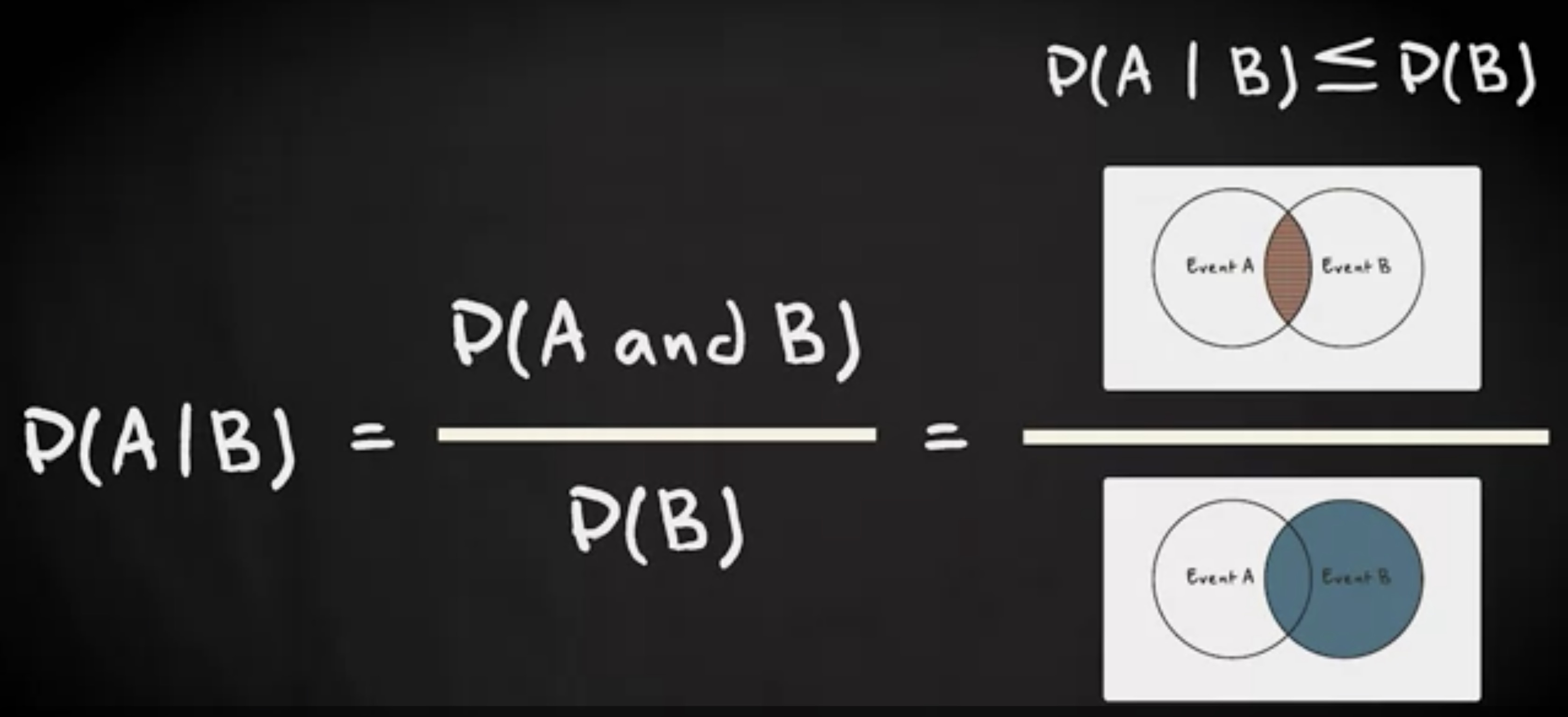
该图强调 A 和 B 的交集概率只能小于或等于 B 的概率。
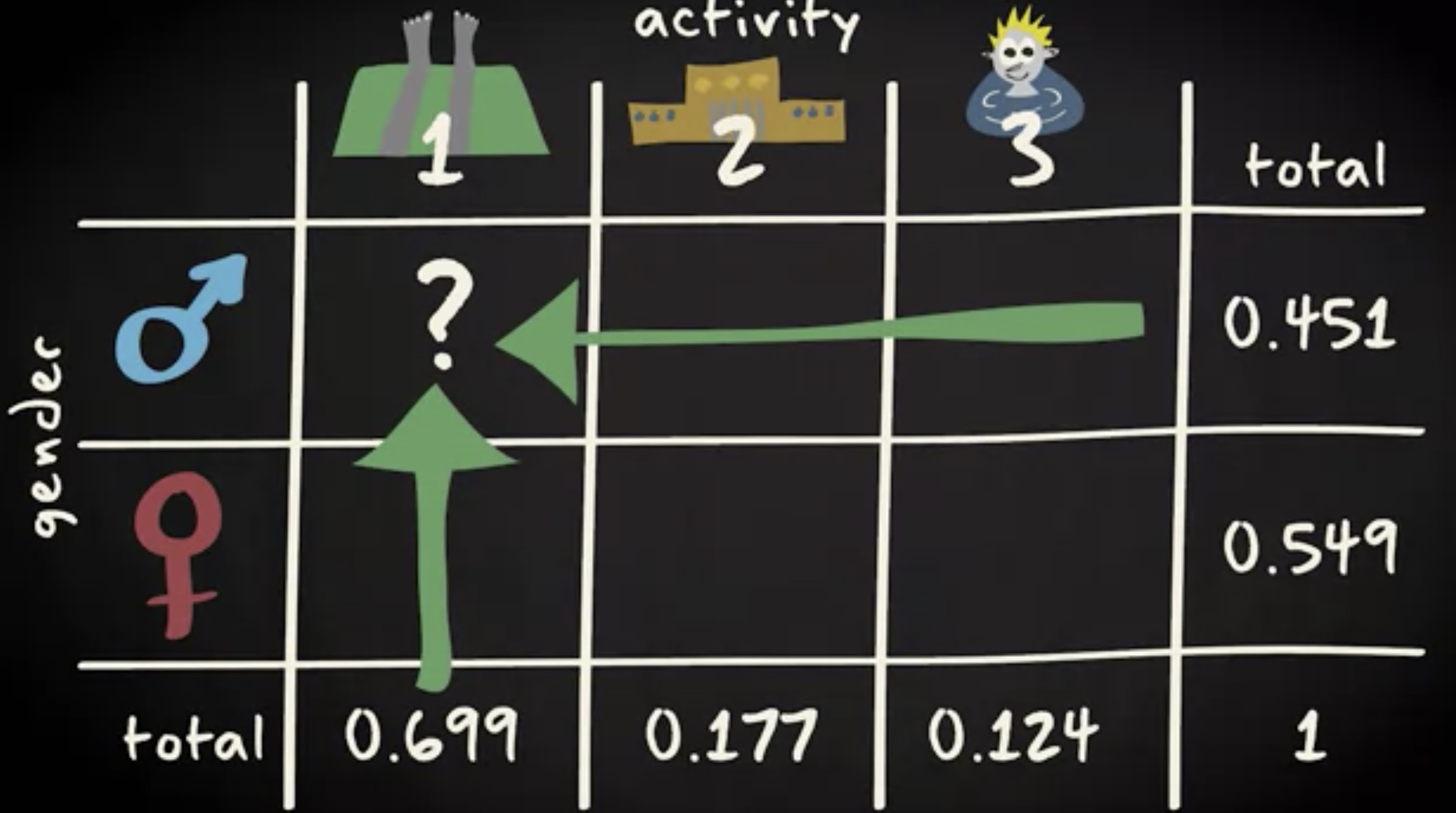
让我们应用方程到一个熟悉的例子。你考虑了沙滩上的人们进行的各种活动,也可以按性别区分人们。将结果转换一张有概率的表。现在,有了这些变量,活动和性别,如何举出一个条件概率的例子?具体来说,是你知道一个结果发生的概率,然后要计算这个结果发生后,其他结果再发生的概率。让我们举一个具体的例子。你将估算一个概率 —— 该人是男性,且则该人正在休息。
为了算得这个概率,应用前面说到的公式,联合概率除以是男性的概率。因此, 0.3 除以 0.45 。
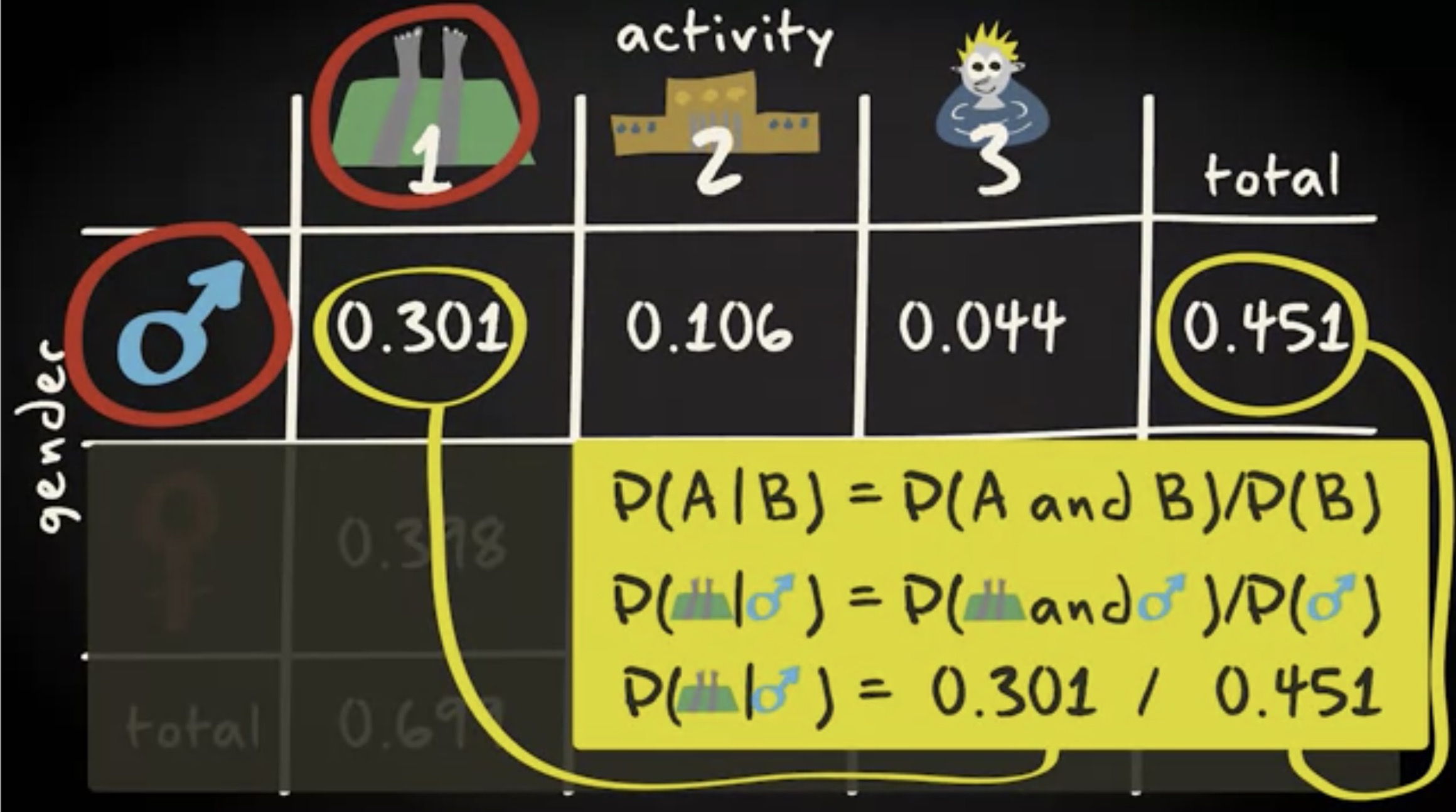
现在我有一个问题要问你。你能计算给定活动的性别概率吗?方法一样:
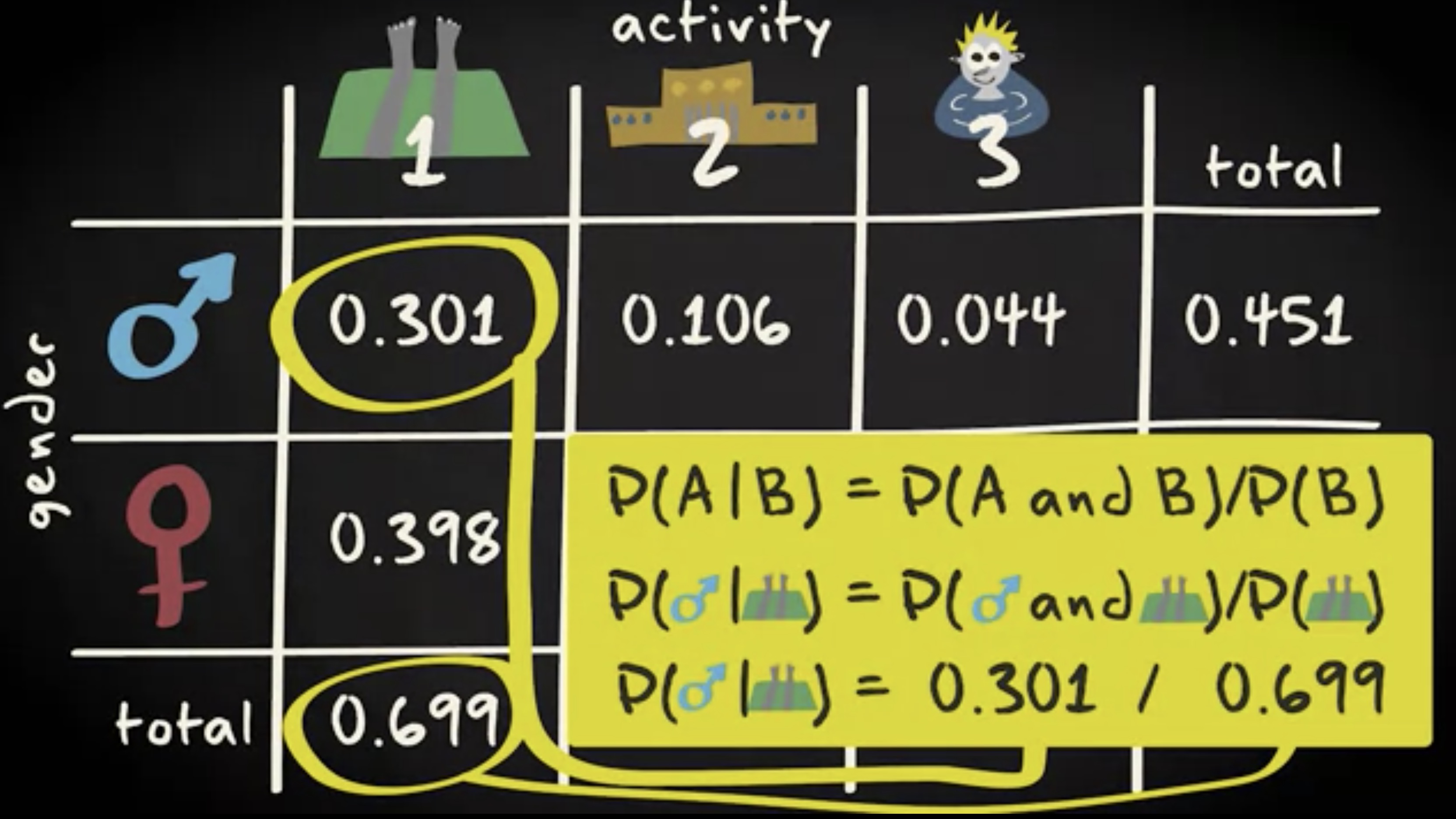
因此,根据联合概率和边际概率,您可以计算出条件概率。虽然条件概率方程很简单,但它还有更多可以挖掘。再看一下方程式,如果两边都乘以事件 B 的边际概率,你就得到了一个计算联合概率的公式。
这其中隐含的意思是,如果交给你一项任务:找到事件 A 和事件 B 的联合概率,如果你不知道 A 和 B 之间是否独立,你需要同时拿到 B 的概率和给定 B 发生 A 的条件概率,或者拿到 A 的概率和给定 A 发生 B 的条件概率。
小结:
- 条件概率是指给定另一件事已发生时某件事的概率。
- 表明上看不是很特别,但条件概率是很多概率估算的核心。
- 数学上,给定 B 的 A 的条件概率等于 A 和 B 的联合概率除以概率 B 。
- 条件概率的定义,也适用于不论是否独立的事件的联合概率。给定 B 的 A 的条件概率可以看成是 B 发生后,样本空间缩小到 B 时 A 发生的概率。

