欢迎关注微信公众号「Swift 花园」
集合基础 —— 理论概念
在这篇教程中,我将介绍一些重要概念,它们是关于 集合 (set) ,即项的数据集。这对于理解概念以及得出概率的计算规则十分有用。同时,集合的特殊性还在于它不仅可用于概率演算,还用在逻辑学中。
让我们开始吧。如之前的教程中提到的,样本空间是随机现象所有结果的数据集。举个例子,抛一枚硬币两次,有四种可能的结果。事件是样本空间的子集。例如,最后一次抛硬币你得到正面朝上。
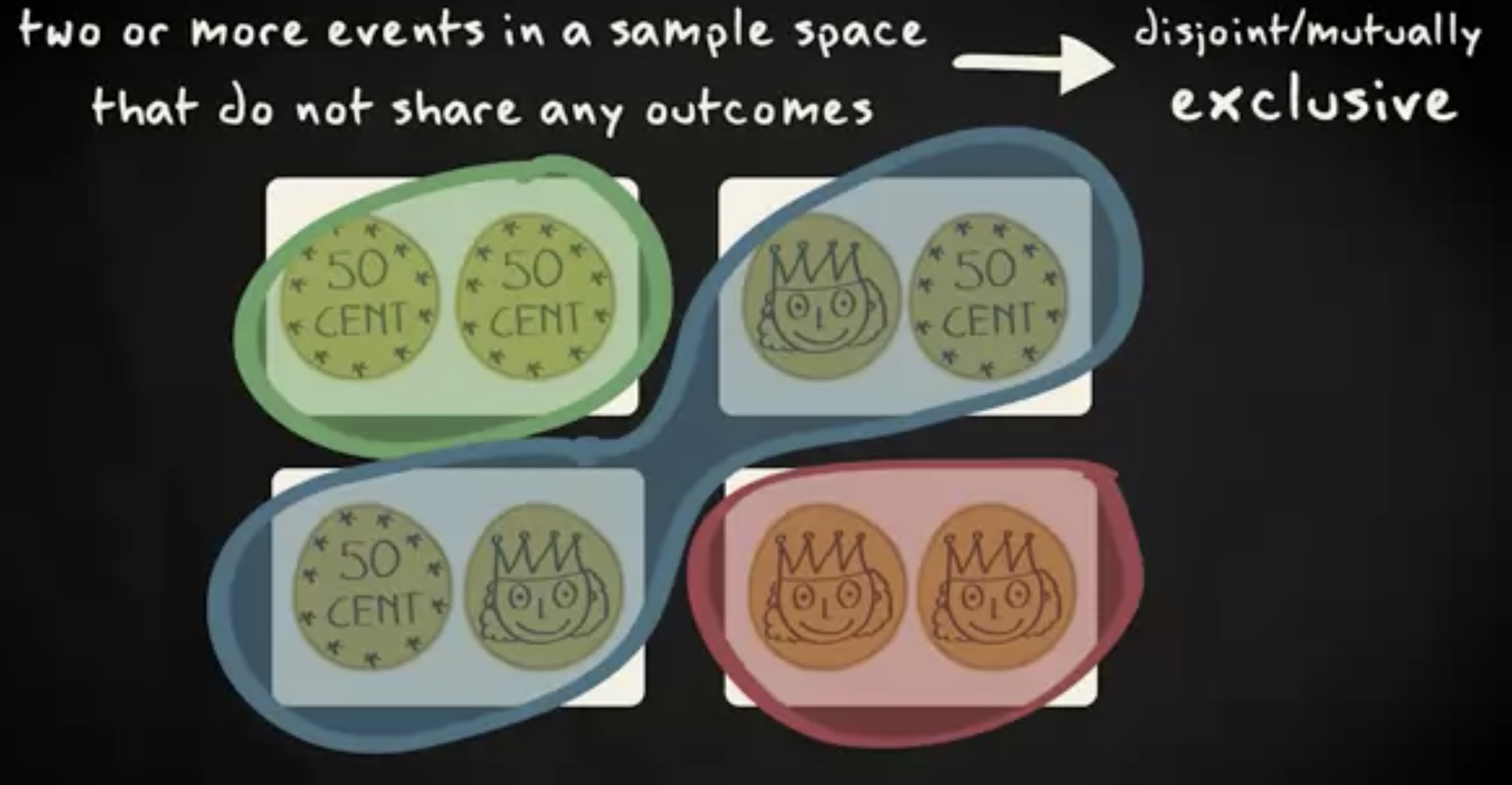
我们看到,一个样本空间可以两个或更多结果完全不同的事件。比如,抛硬币两次,0 次正面朝上,1 次正面朝上, 2 次正面朝上。它们被称为 互斥 (disjoint) 的事件。另外一个术语叫 互不相容 (mutually exclusive) 。
有一对特殊的互斥事件,某个事件和它的对立面 (即这个事件不发生的事件)。这种上下文中,对立的事件被称为 补集 (complement) 。比如,这里可以是没有正面朝上和其他三种情况互为补集。

你也可以有多个事件共同填满完整的样本空间。这些事件被称为 完全穷尽 (collectively exhaustive) 事件。如果它们彼此不重叠,就是 相互独立,完全穷尽 (disjoint collectively exhaustive) 。互斥事件相关联的概率之和小于或者等于 1 ,完全穷尽事件的概率之和等于 1 。

直觉上很容易理解这些概念,它们可以通过 文氏图 (Venn diagrams) 来表达。文氏图通过简单的几何形状来呈现集合或者集合的部分。
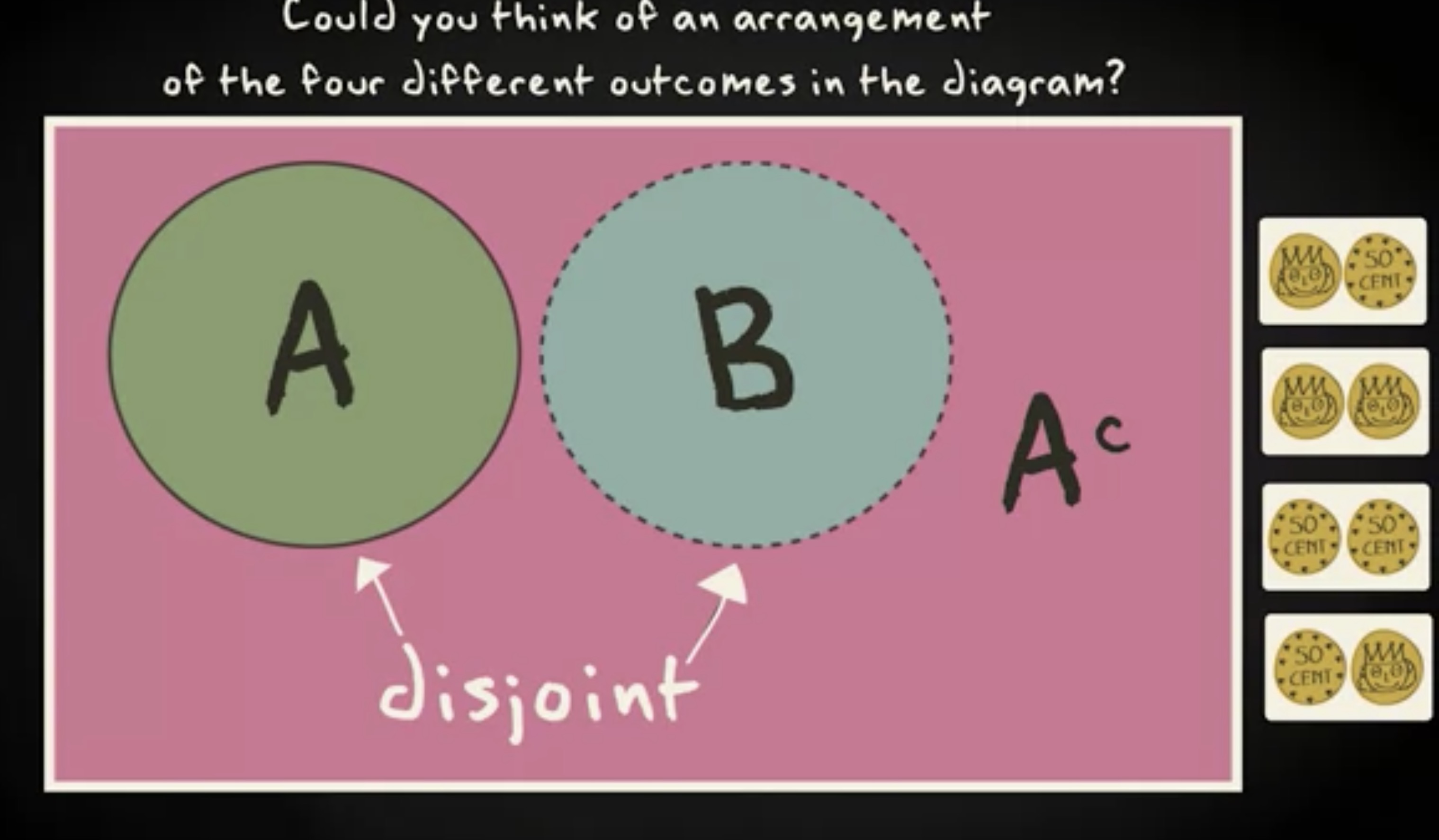
这些矩形描绘同一个样本空间,在空间中,有一个事件 A ,剩下的部分都是事件 A 的补集。同一个样本空间里,还有另外一个事件 B ,和 A 不重叠。因此它们两者是互斥的。
如果我们把这个文氏图应用于两次抛硬币的实验,你能把四个不同的结果放进图中并且描述事件吗?
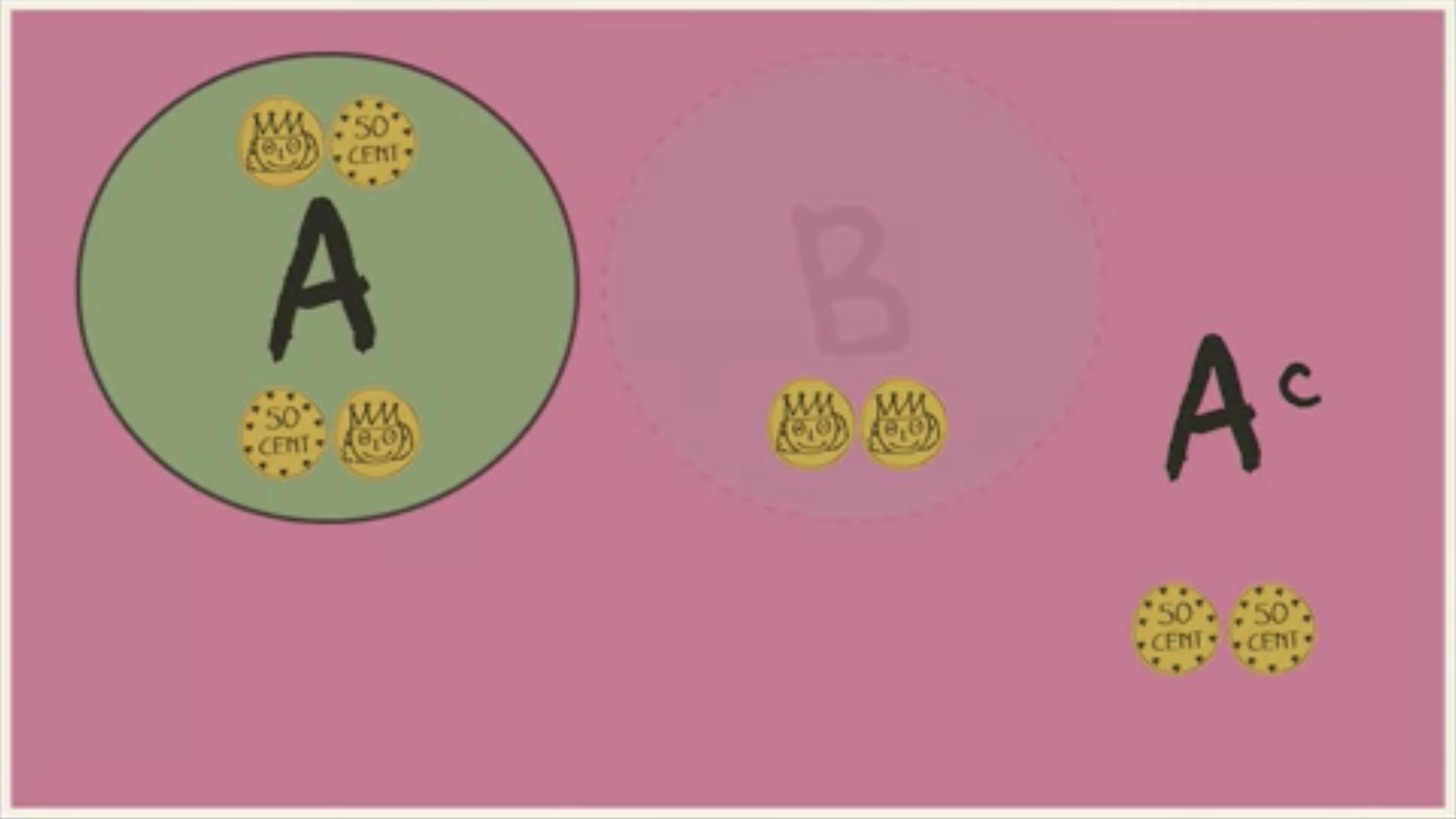
可以是这样的,只有一次正面朝上是事件 A ,有两次正面朝上是事件 B 。 A 的补集会包含两次反面朝上和两次正面朝上。
还用文氏图,两次抛硬币的实验也可以是这样的:
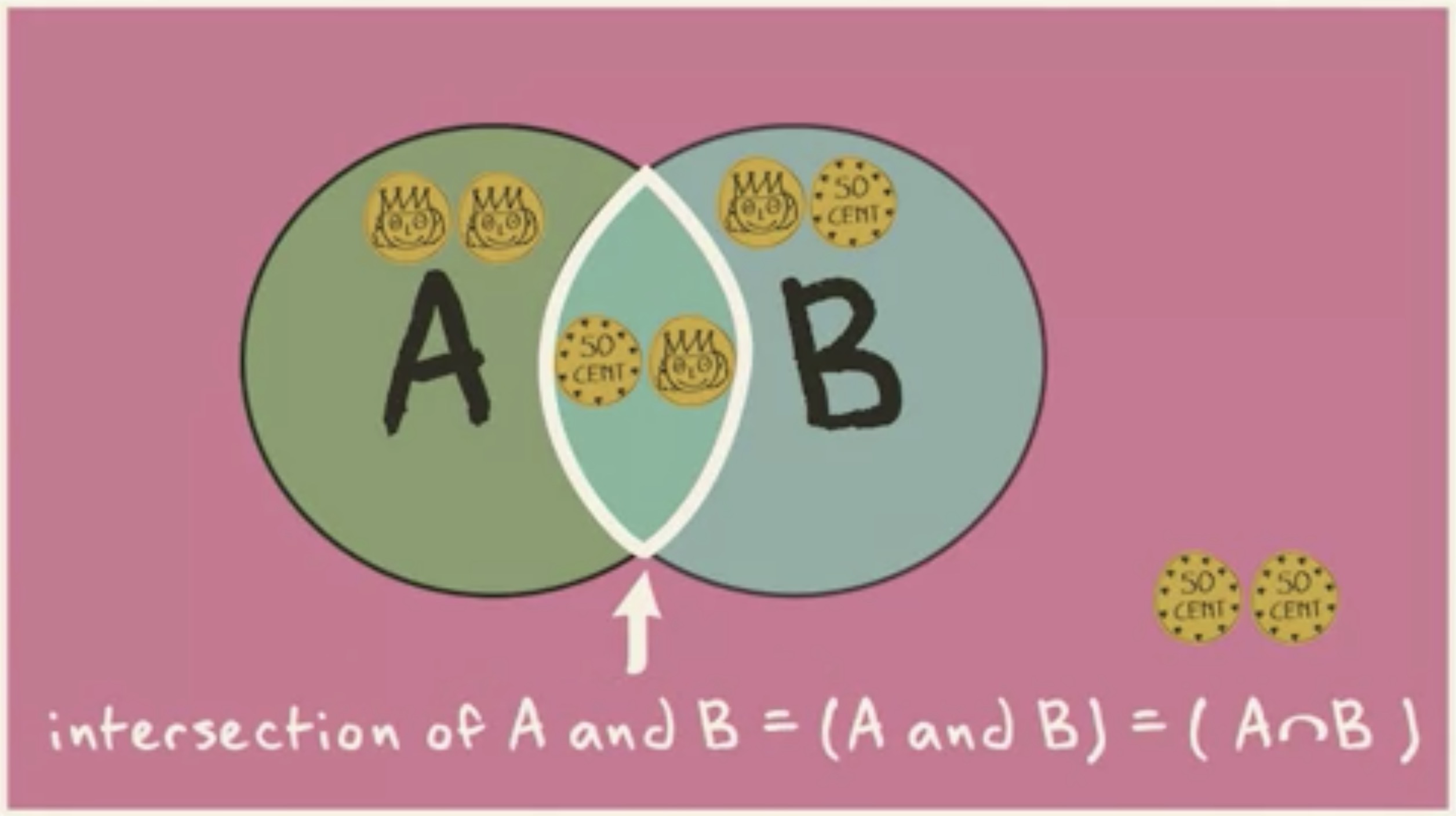
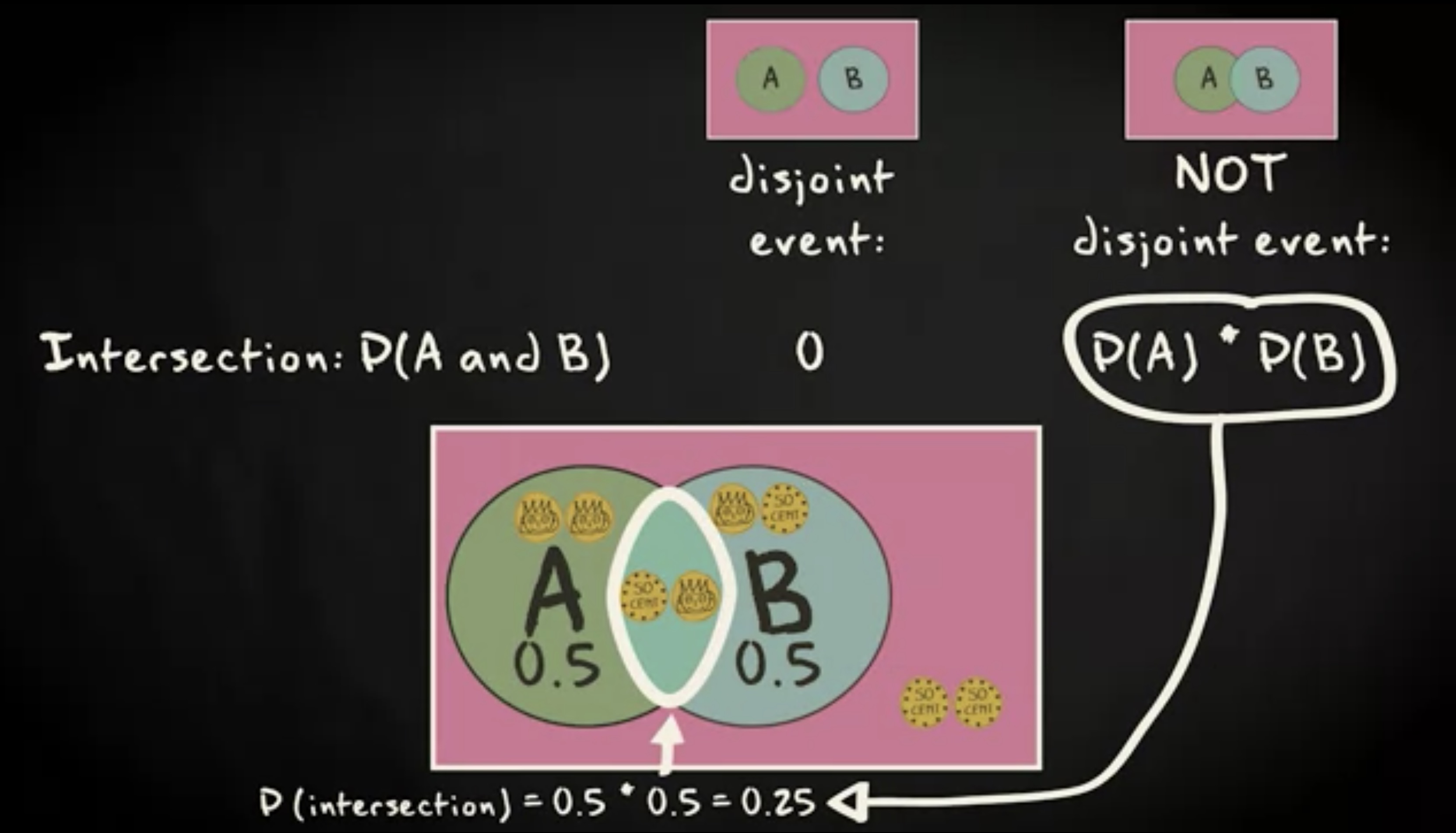
两个事件, A 和 B ,相互之间有重叠。 A 是事件 “第二次结果是正面朝上”, B 是事件 “只有一次正面朝上”。结果 “反面,正面” 会同时落在两个事件之内。“反面,反面” 也属于样本空间的一部分,但不落在 A 和 B 任何一个事件内。两个事件重叠的部分被称为 交集 (intersection) 。
事件 A 和 事件 B 的交集可以速记为:
现在,让我们来找出两个事件交集的概率。如果两个事件是互斥的,事件很简单。交集的概率为 0 。如果两个事件并不互斥,即它们重叠,事情就稍微有点复杂。
假定我们正在处理的是独立事件。也就是说,例子中抛出第二个正面的事件的概率不受只抛出一个正面的事件的影响。对于独立事件 A 和 B ,它们的交集的概率是两者各自概率的乘积。
这里,事件 A 有两种情况,所以概率是 2 / 4 。事件 B 的情况相同,概率也是 2 / 4 。因此,最后的交集的概率等于两者概率乘积,也就是 1 / 4 。
小结
- 样本空间中不共享任何结果的事件被称为 互斥事件 或者 互不相容 。
- 多个事件一起填满整个样本空间,则把它们称为 完全穷尽 事件。
- 如果样本空间里只有两个互斥事件构成完全穷尽,那么它们互为 补集 。
- 互斥事件的概率之和小于或者等于 1 。完全穷尽事件的概率之和等于 1 。
- 事件 A 和 B 的 交集 同时是两个事件的一个子集,这个子集包含了 A 的一部分,并且这部分也是 B 的一部分。独立事件 A 和 B 的交集是通过事件 A 的概率和事件 B 的概率乘积来计算的。对于互斥事件,按照定义,交集属性等于 0 。
并集
这一节中,我将介绍 并集 (Union) 的概念和并集的概率。并集在现实生活中会导致一个比其各个部分集合的总和具有更多新属性的实体吗?很遗憾,在概率理论中,这种魔力是不存在的。并集只是
需要特别注意 —— 不要将事情加倍计算。
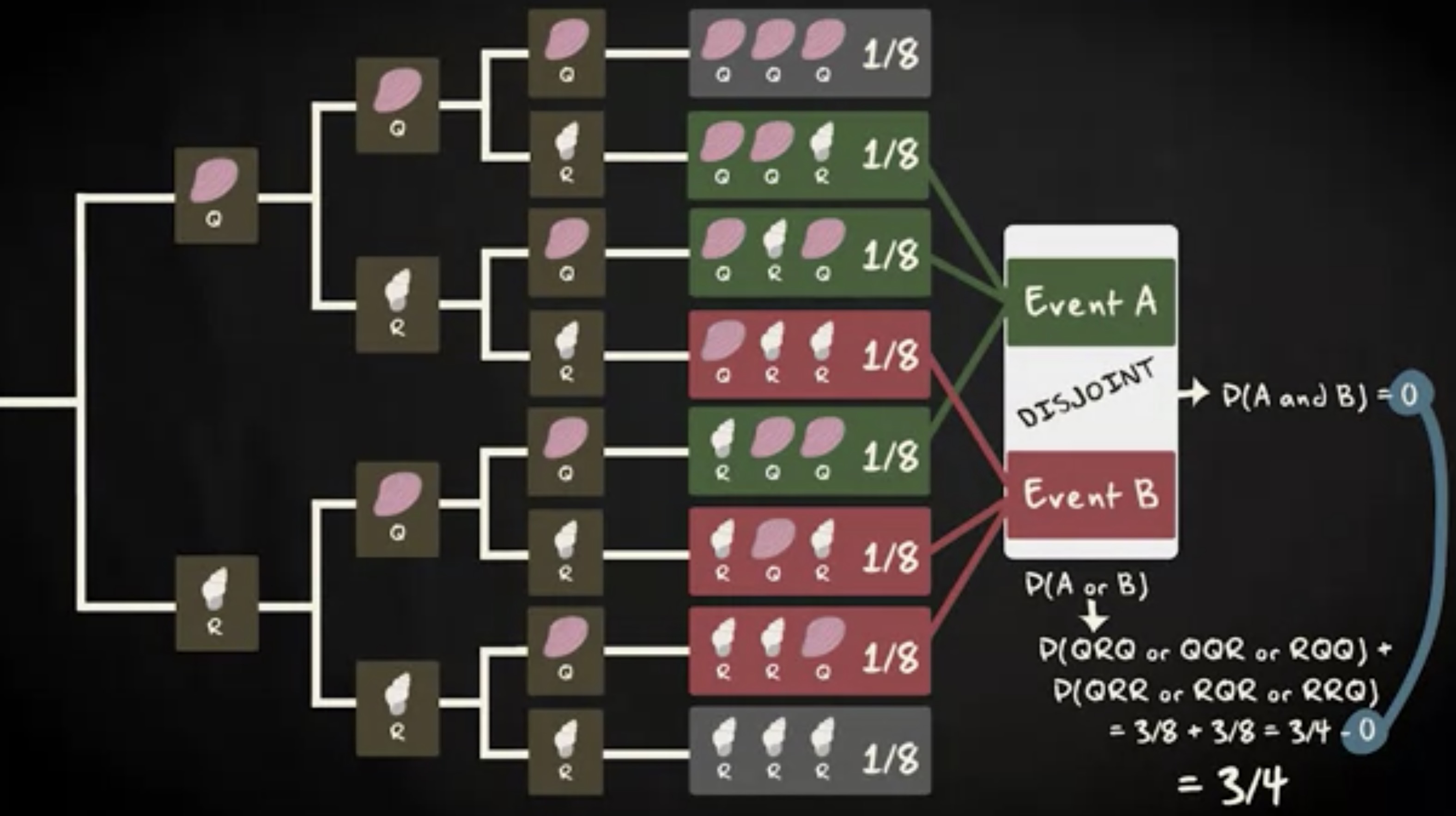
还是贝壳的例子,你在海滩上随机捡三个贝壳。周围只有两种贝壳, Q 和 R 。两种类型的贝壳数量相等并且你可以认为有无数。在这种情况下,样本空间包括八个结果。整个实验的树形图如下。

获得任何组合的概率的八分之一。让我们设定,总共捡起一个 R 贝壳作为事件 A ,总共捡起两个 R 贝壳作为事件 B 。如果我们对事件 A 发生或事件 B 发生,或者 A 和 B 同时发生感兴趣。

以这种方式组合事件被称为 “并集”,速记为:
要计算关于事件 A 和 B 的并集的概率,你必须求出两个事件的总和,然后减去 A 和 B 的交集。减去交集的原因是它被计数了两次。拿到一个 R 贝壳的概率 —— 事件 A ,是八分之三。
拿到两个 R 贝壳的概率同样也是八分之三,它们的总和是八分之六,即四分之三。
实际上,事件 A 和 B 不分享任何结果,即他们不相交的,则他们的交集概率为零。因此,并集的概率是四分之三。
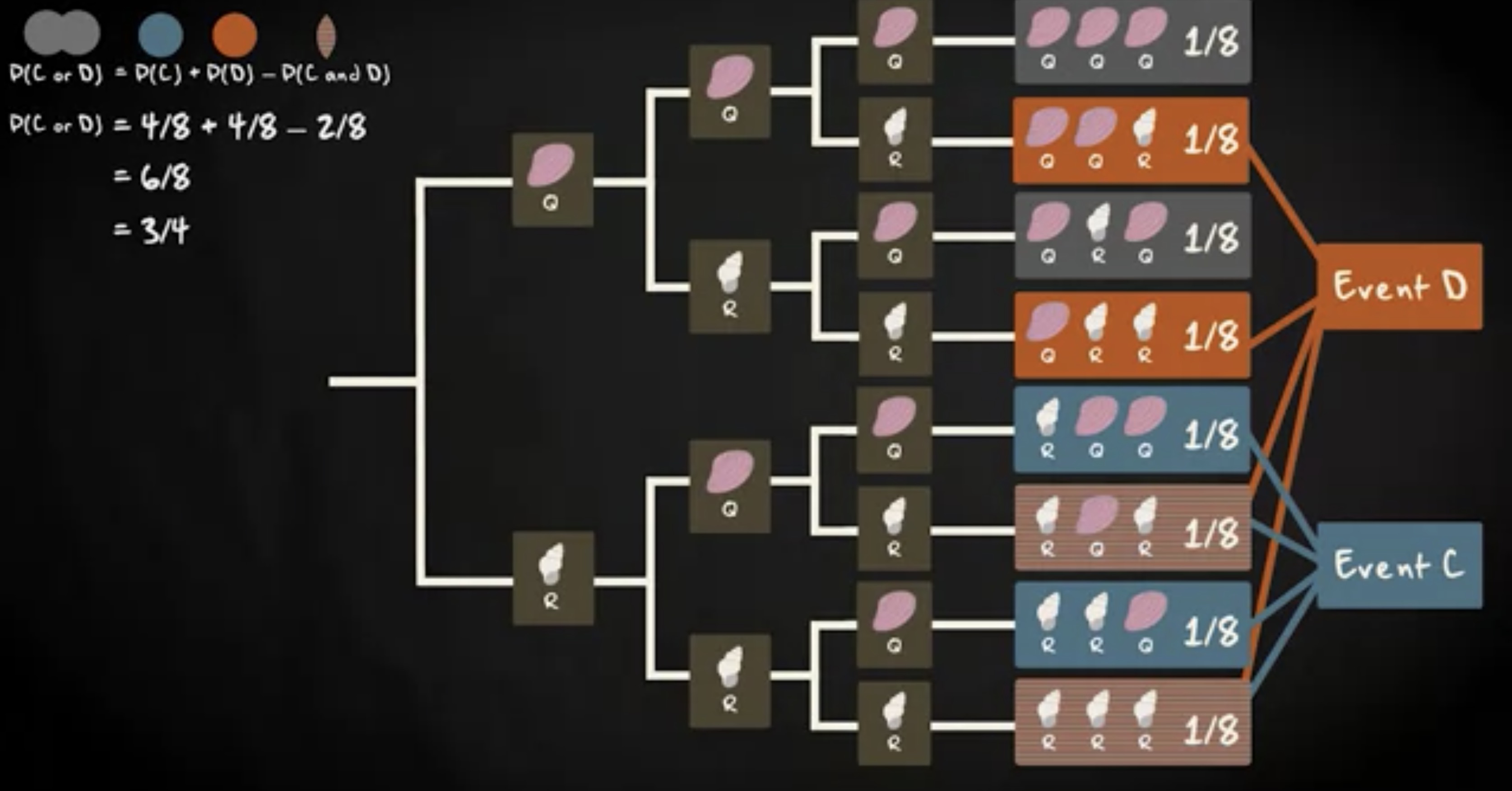
现在,考虑两个不同的事件。 事件 C ,你选择的第一个贝壳将会是 R 贝壳。事件 D ,最后一个贝壳 是 R 贝壳。显然,这两个事件不是互斥的,因为它们有重叠。事件 C 和 D 的交集包括
第一个贝壳是 R 贝壳,同时第三个贝壳也是 R 贝壳的情况。

通过将 C 的概率加到 D 的概率,再减去 C 和 D 的交集来找到 C 和 D 的并集,是四分之三。
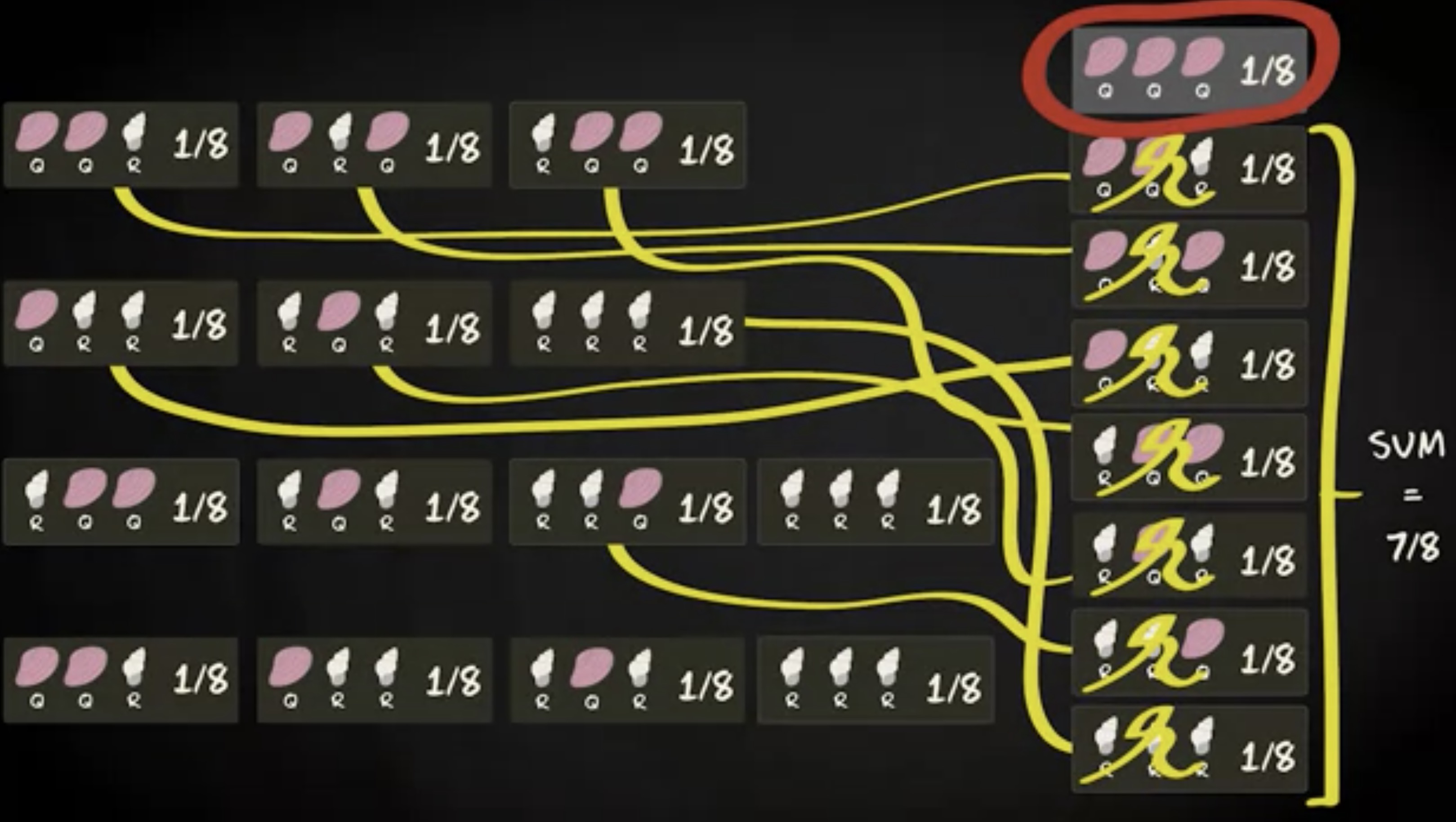
现在挑战升级 —— 事件 A , B , C 和 D 的并集是?如果你把方程式机械地应用过来,事情会有些乏味,因为会有不少加法和减法的计算。

不过,由于总的样本空间中并没有特别多的基本事件,这里有一个更简单的方法。你可以列出八个
基本事件,然后检查它们出现在四个组合事件中的哪一个。最后,你会发现只有一个基本事件不发生在组合事件中。从四个组合事件来看,有七个基本事件的结果是四个组合事件中的某一个的部分。因此,并集的概率是这七个基本事件之和,即八分之七。
小结
- 多个事件的并集是这样一个事件:它包含原始事件的所有结果,并且没有重复。
- 几个事件的并集概率是各个事件的概率之和减去事件之间的交集的概率。
- 对于两个事件,等式为 $ P (A \cup B) = P (A) + P (B) - P (A \cap B) $ 。如果事件 A 和 B 互斥,则交集的概率为零。并集方程简化为 $ P (A \cup B) = P (A) + P (B) $。

