欢迎关注微信公众号「Swift 花园」
随机变量的平均数
在了解了随机变量的概率分布之后,我们可以开始对这种变量进行计算了。
首先,你需要知道,总结性统计 (summary statistics) ,跟观测数据相似,都能用来捕捉分布的本质。这一节中,我们要来研究概率分布的平均数,以及我们在调整随机变量或者组合随机变量之后,平均数如何变化。
以下将一个随机变量的平均数以 $ μ $ 注记,它表示对许多观测值预期的平均结果,因此也被称为随机变量的 期望值 (expected value) ,以 $ E $ 注记。
一个离散随机变量的平均数是所有可能的值乘以概率权重之后的均值,因此它等于每个可能的值乘以概率,然后加总。对于连续随机变量,同样的规则也适用。为了应对连续性,加总的计算被替换成积分 (integral) ,概率也不像离散那样被定义为 i ,而是 x 的函数。
举个例子,假设你正在一个熟悉的街区日常漫步,路上会经过三个交通灯。每等一个交通灯会使整个漫步多花 2 分钟。对于这三组交通灯的等待,你记录了等 0 个 到等 3 个的频率,下面是概率表:
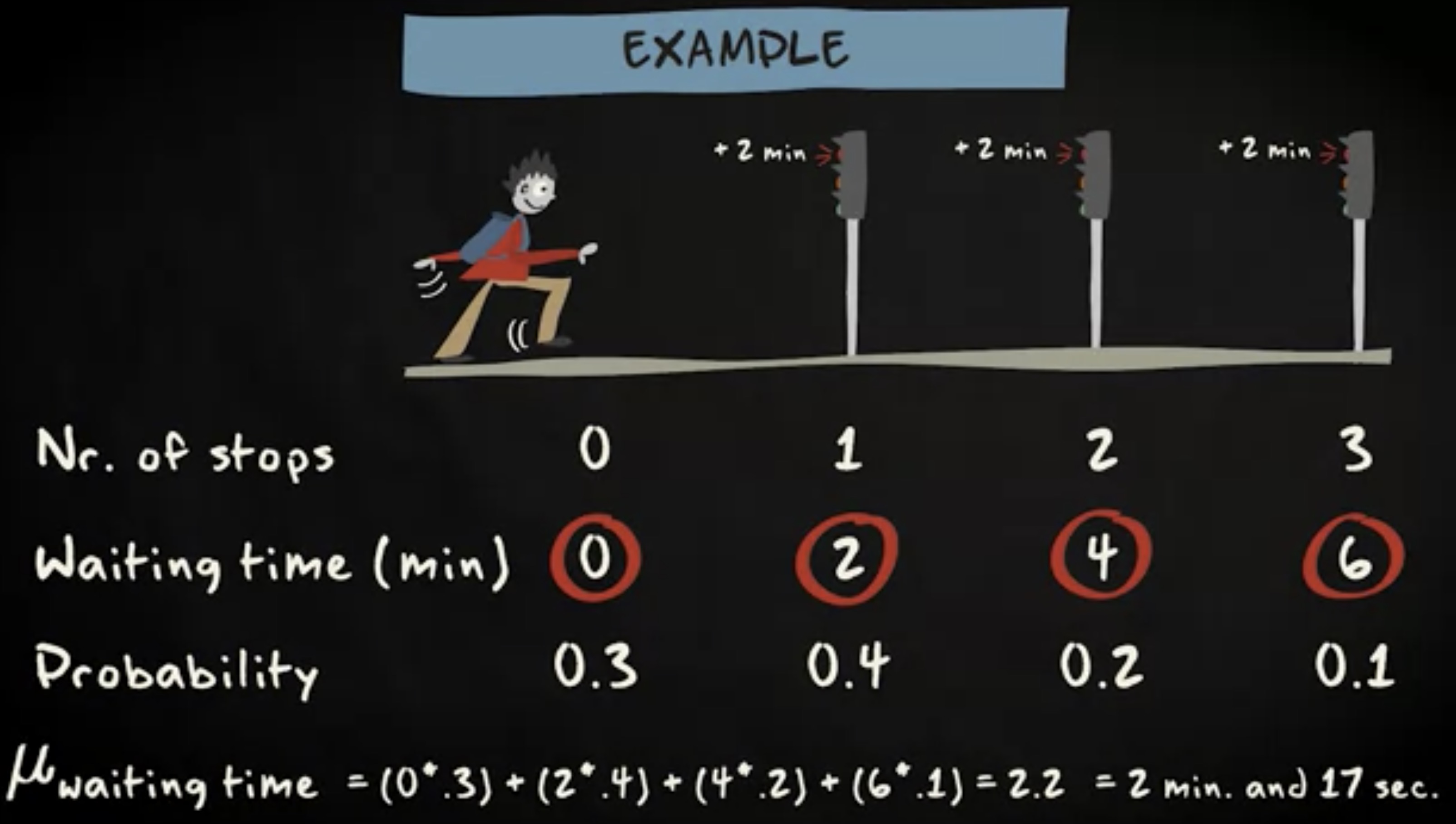
你预期的等待时间计算方法如下,最后会得到 2 分 12 秒。有趣的是, 2 分 12 秒这个值实际永远不会发生。你要么不用等,要么就是等 2, 4, 6 分钟中的某个时间。
现在,让我们来审视一下随机变量的平均数。如果我们给随机变量 x 乘上一个系数再加上一个值, 变成 $ a + bx $ ,那么平均值会变成 $ μ_{a+bx} $ 。
现在回到我们的例子。由于你找到一条捷径,旅程节省了一分钟。但同时,交通灯变得更忙了 —— 等待时间增加到 2 分 30 秒,即增加了 25% 。你抄近路省出的时间对应方程里的 a ,等待时间增长系数 1.25 对应 b 。新的概率分布通过下面这张表格呈现。
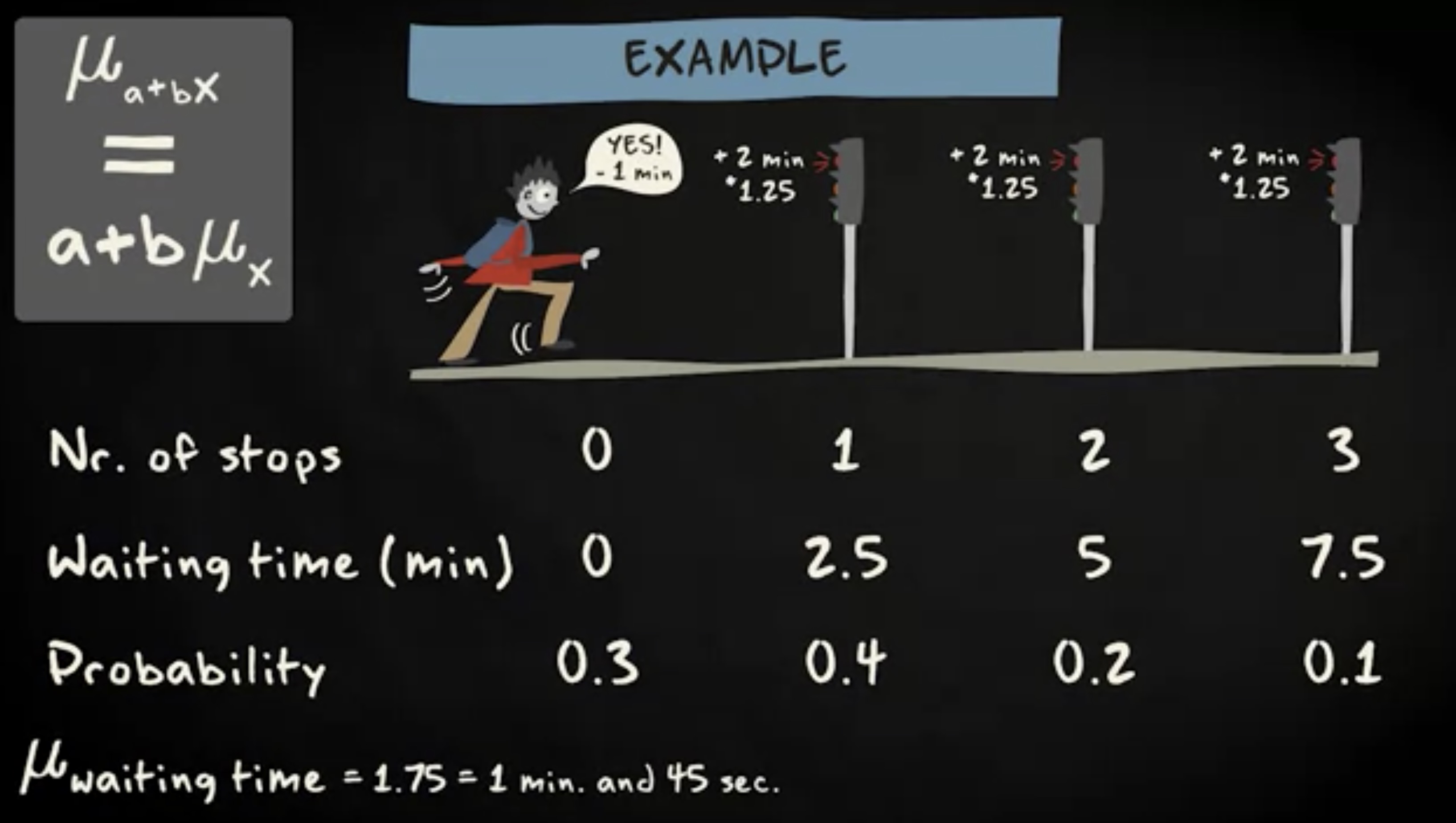
新的等待时间平均值变为 1 分 45 秒。
现在让我们来看看两个随机变量相加或者相减的时候回发生什么。结果是:两个相加或者相减的随机变量的平均值也是它们各自平均值的简单求和或者求差。这个结论甚至不要求两个变量相互独立。

举个例子,假设你想要计算一个礼拜的等待时间的平均值,那你只需要把每天的平均值加起来就可以了:
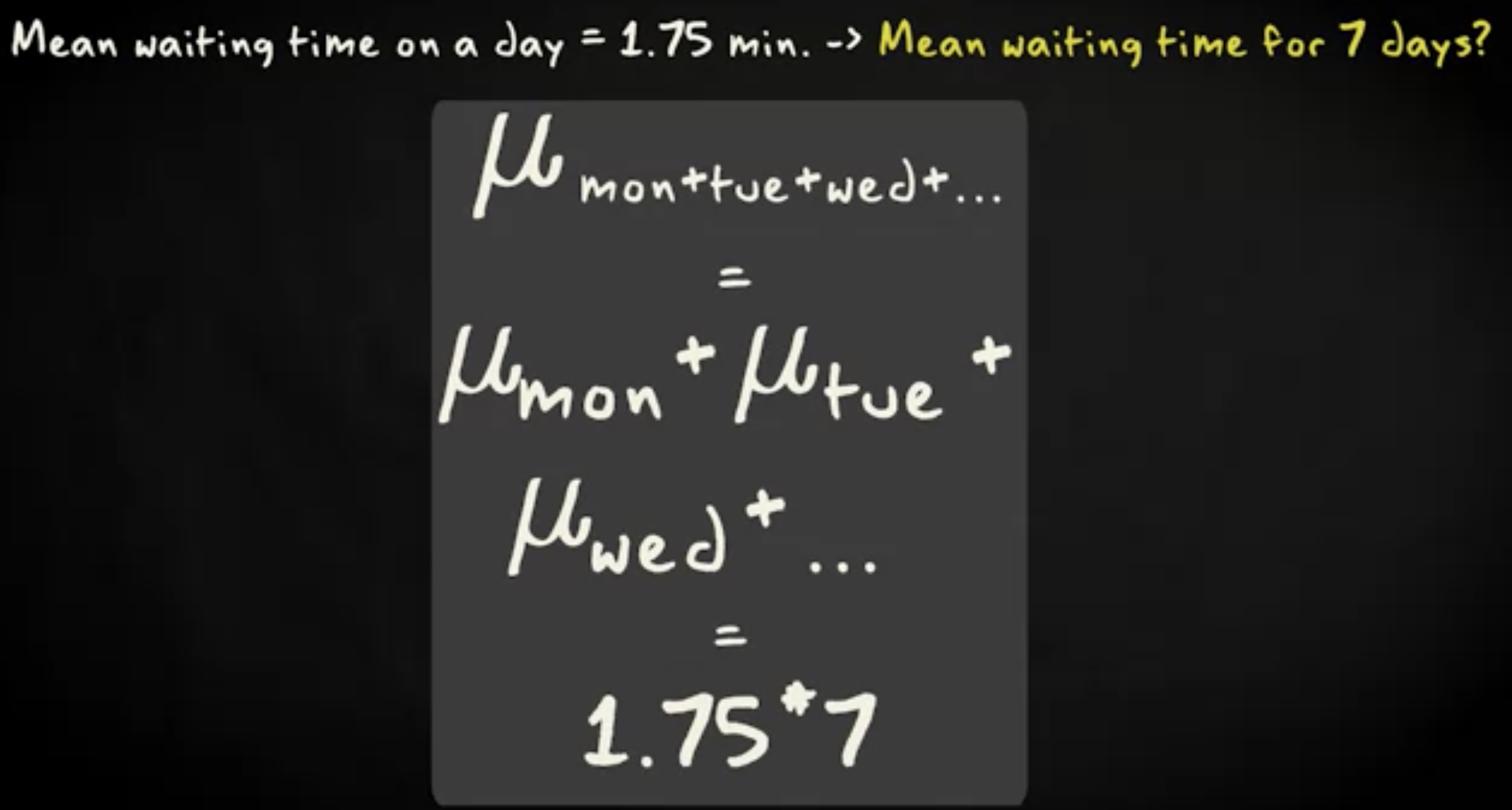
小结
- 平均值,或者一个离散随机变量的期望值,是变量所有可能的值乘以它们的概率,然后求和。如果随机变量通过乘法或者加上常数改变,那么平均值会发生相同的变化。
- 几个随机变量的平均值加总在一起是它们平均值的总和,即便这几个变量在统计上不一定是独立的。
随机变量的方差
在平均数之后,你需要了解的第二个总结性统计指标是随机变量的方差,即离散程度的度量。
这一节中,我们要来研究概率分布的方差,以及我们在调整随机变量或者组合随机变量之后,方差如何变化。
一个随机变量 X 的方差 var (X) 是以它与平均值的差值的平方的期望来定义的:
如果你想基于概率分布算出方差,它其实是变量可能的值与平均值之差的平方,然后加总或者积分。
连续随机变量的方差:
离散随机变量的方差:
连续随机变量的方差比较复杂一些,用到了积分。离散随机变量看起来就简单一些。
举个例子,这个离散分布给出了一年中你可能遭遇交通事故的风险。平均风险是 0.04 ,即每 25 年一次。

首先,你计算出事故次数和平均值之差,然后平方,乘上对应的概率,最后加总。事故风险的方差看起来接近 0.06 ,标准差 0.24 左右。
现在,让我们来看看,如果通过给随机变量加一个 a 或者乘以 b ,方差会发生什么变化。

当你将两个 a 放定义方差的等式中变换时,你会发现常量 a 消失了,而因子 b 被平方了。因此,通过加或者减一个值到随机变量,它的方差不变。但通过乘以一个数 b ,它的方差会变成原始方差乘以 b 的平方。标准差,即方差的平方根,则跟随因子 b 一起变化。
举个例子,你是否经历过晴天人们更愿意跟你打招呼,阴天更不爱搭理你的情景呢?下面图中上方是一个阴天时你走在街上每分钟遇到的点头或者微笑次数的分布。平均每分钟 1.4 次,方差 0.84 。而图中下方是晴天时的数据,你发现大家变得更友好了,具体来说,友好的倍数是 2 。

理论告诉我们,平均值应该变成 2 倍于 1.4 ,即 2.8 ,而方差应该变为 4 倍,即 3.36 。让我们检视一下新的分布的方差。
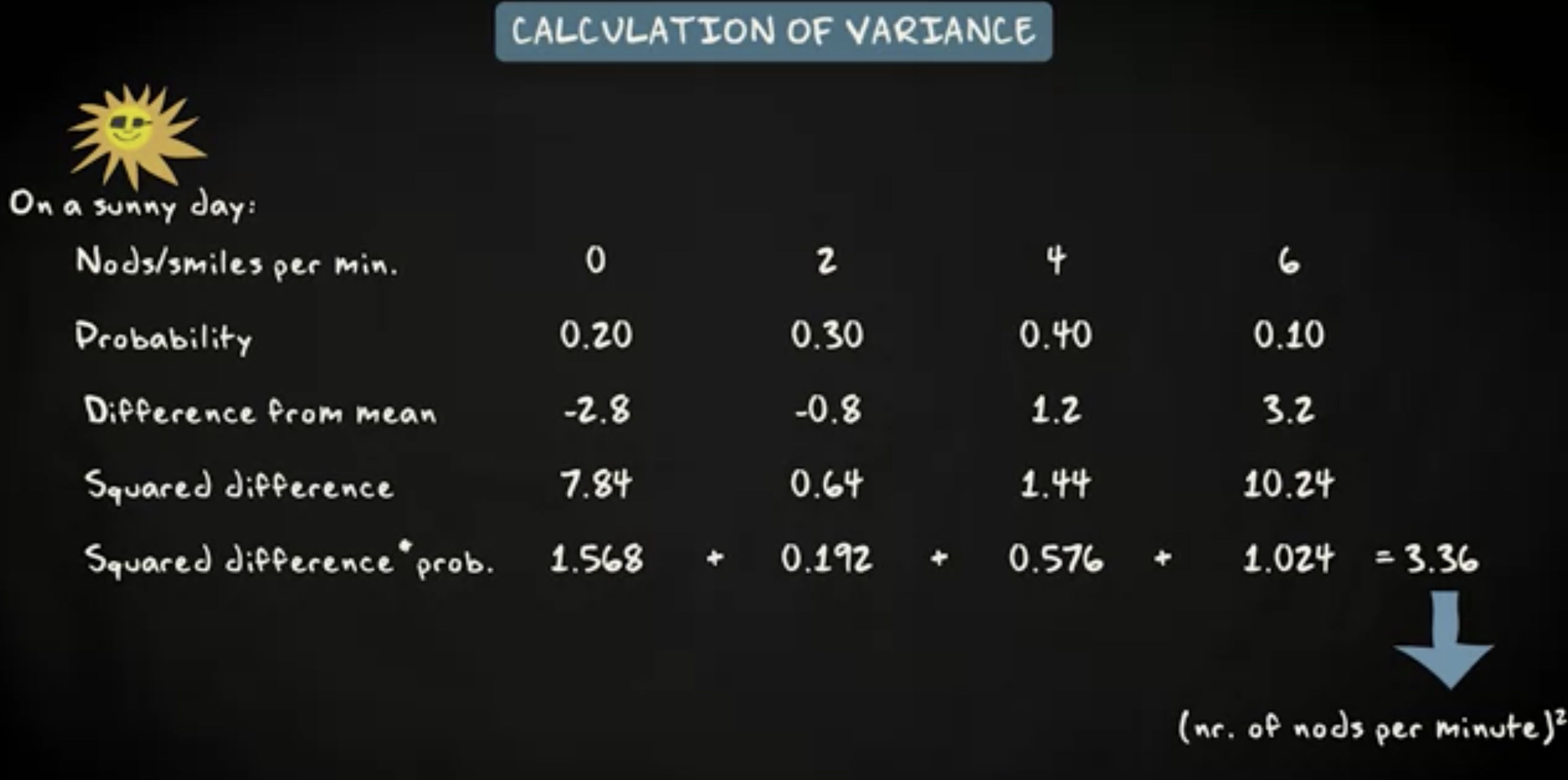
这个表格展示了具体的步骤。从微笑或者点头次数减去平均值得到差值,平方,乘以概率,最后加总,确实是 3.36 。
现在让我们来看看如果把两个随机变量相加或者相减会怎么样。对于随机变量 X 和 Y ,两者之和的方差是两者各自方差的和再加上 2 乘以 X 和 Y 之间的 协方差 (covariance) 。而两者之差的方差是两者各自方差的和再减去 2 乘以 X 和 Y 之间的协方差。

下面这两个更完整的等式则适用于 X 和 Y 各自有因子 a 的情况。

这些等式适用于任意两个相加或者相减的随机变量,而且显而易见,它们要求你知道两个变量之间的协方差。然而,协方差信息通常是不可得的,因此我们这里不考虑通用的情况,而是先考虑一个更严格的案例,即变量之间不相关的情况。这样会使问题简单很多,因为两个不相关变量之间的协方差是 0 ,后面 1 项就从等式中消失了。

因此,在不相关变量之间,相加或者相减都无关紧要了,方差总是两个方差之和。你还可以把等式泛化到任意多个随机变量之和。

还有一个值得注意的点是,随机变量相加的标准差总是小于独立的随机变量标准差相加之和。这看起来很合理,因为随机变量结合之后,有一些变异性会被抵消。
小结
- 随机变量的方差,是这个变量所有可能的值减去它的平均值,乘以概率,然后平方,最后加总或者积分。
- 给随机变量增加常量不会改变方差,但因子会导致方差变为因子平方倍。
- 几个不相关随机变量相加或者相减的方差等于这些变量各自方差之和。标准差是方差的平方根,因此为了得到调整后的标准差,你需要先得到调整后的方差。

