欢迎关注微信公众号「Swift 花园」
随机变量和概率分布
随机变量的随机性其实并不像它的名字传递的那样多。这一节教程中,我将通过随机变量的可能结果和它们对应的概率来描述 概率分布 (probability distribution) 。换句话说,随机分布使随机性具体化,并且提供了一条在计算中使用随机变量的道路。当我们观察个体或者对象的时候,我们可以关注每个个体的若干个属性,这些属性就叫做 变量 。
现在,想象你收集了一份数据,并且决定重复实验。你能够找到相同的试验个体来测量变量,或者能找到相近的个体。不管采用哪一种,你会发现你的变量的值每次都不一样。这就是所谓的变量。举个例子,你测量一个人的身高几次,每次的结果可能会有几毫米到 1 厘米的偏离,这取决于你测量的时间在一天中的时刻,你的测量设备的精度,等等。
通常我们预料变量的值具有随机的变异性。如果这种概率的随机性是中肯的,则这个变量被称为 随机变量 (random variable) 。随机变量可以有一组可能的值,每个值都和概率关联。因此,如果随机变量的样本足够大,不同值的相对频率就接近概率。为了让表达更清晰,让我们用斜体的大写字母来表示随机变量,小写字母来表示它取到的值。
即 X 为随机变量,$ x_1, x_2, x_3, … $ 为随机变量的值。
随机变量有两种,一种是 离散的 (discrete) ,一种是 连续的 (continuous) 。离散随机变量可以有一组可数数量的不同值,比如 0 / 1 / 2 / 3 。实际上,如果一个随机变量只能取得有限数量的不同值,那它必定是离散的。离散随机变量的例子很多,比如一个家庭里小孩的数量。连续随机变量则可以取得无限数量的可能值。它通常是测量。为了演示无限性,假设一个身高值测出来是 3.1 米,如果换更精确的测量仪器,也许能测到 3.14 米。更精确的仪器,也许还能测到 3.145 米。换言之,通过更精确的测量,或者放大操作,无限数量的结果是可能的。年龄,温度,速度,这些都可以是连续随机变量的例子。
随机变量的值可以很方便地通过随机分布来呈现。随机分布的呈现形式可以是表格,图或者数学方程,并且是通过随机变量的每个取值关联的概率列表来定义的。
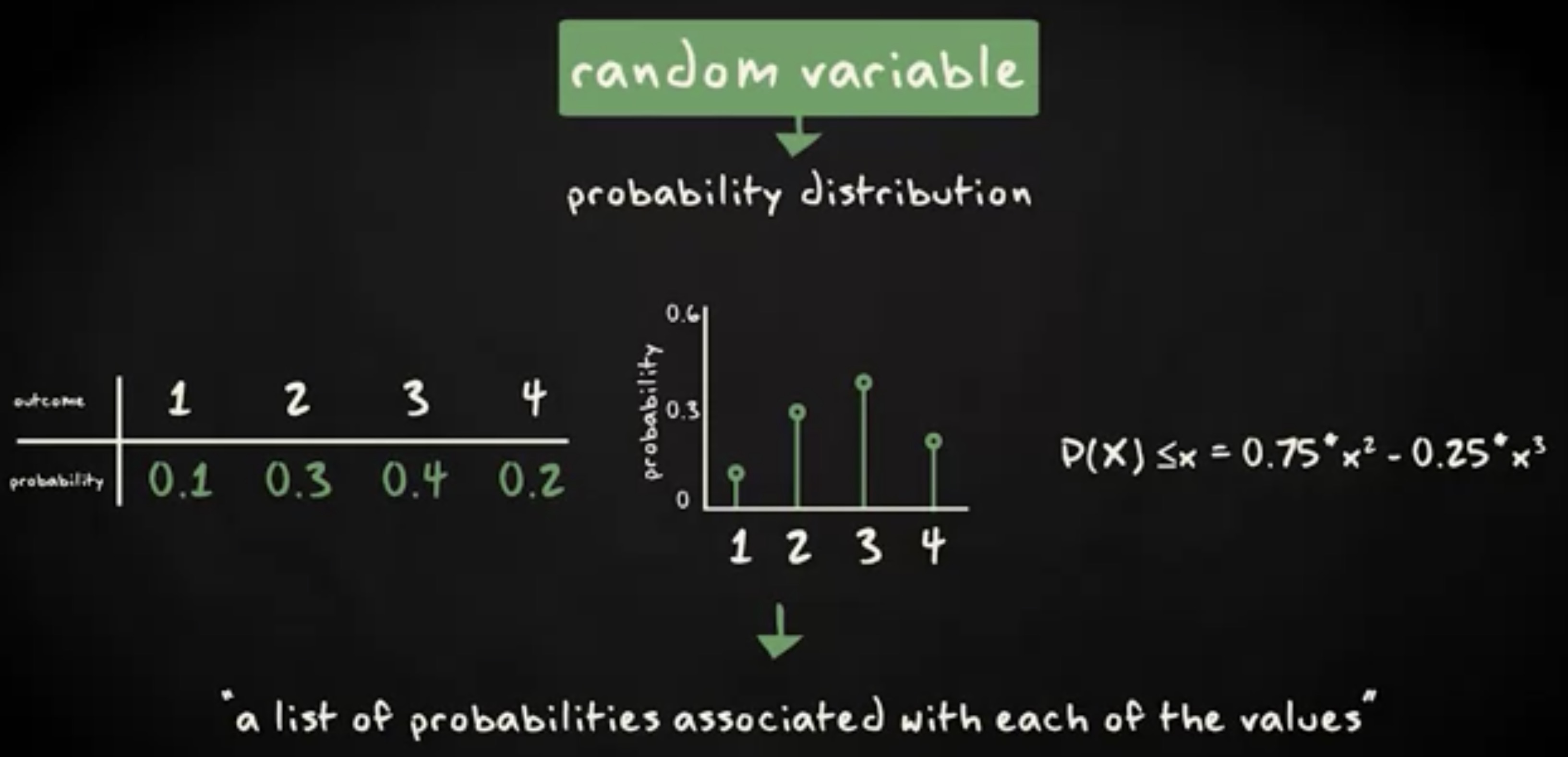
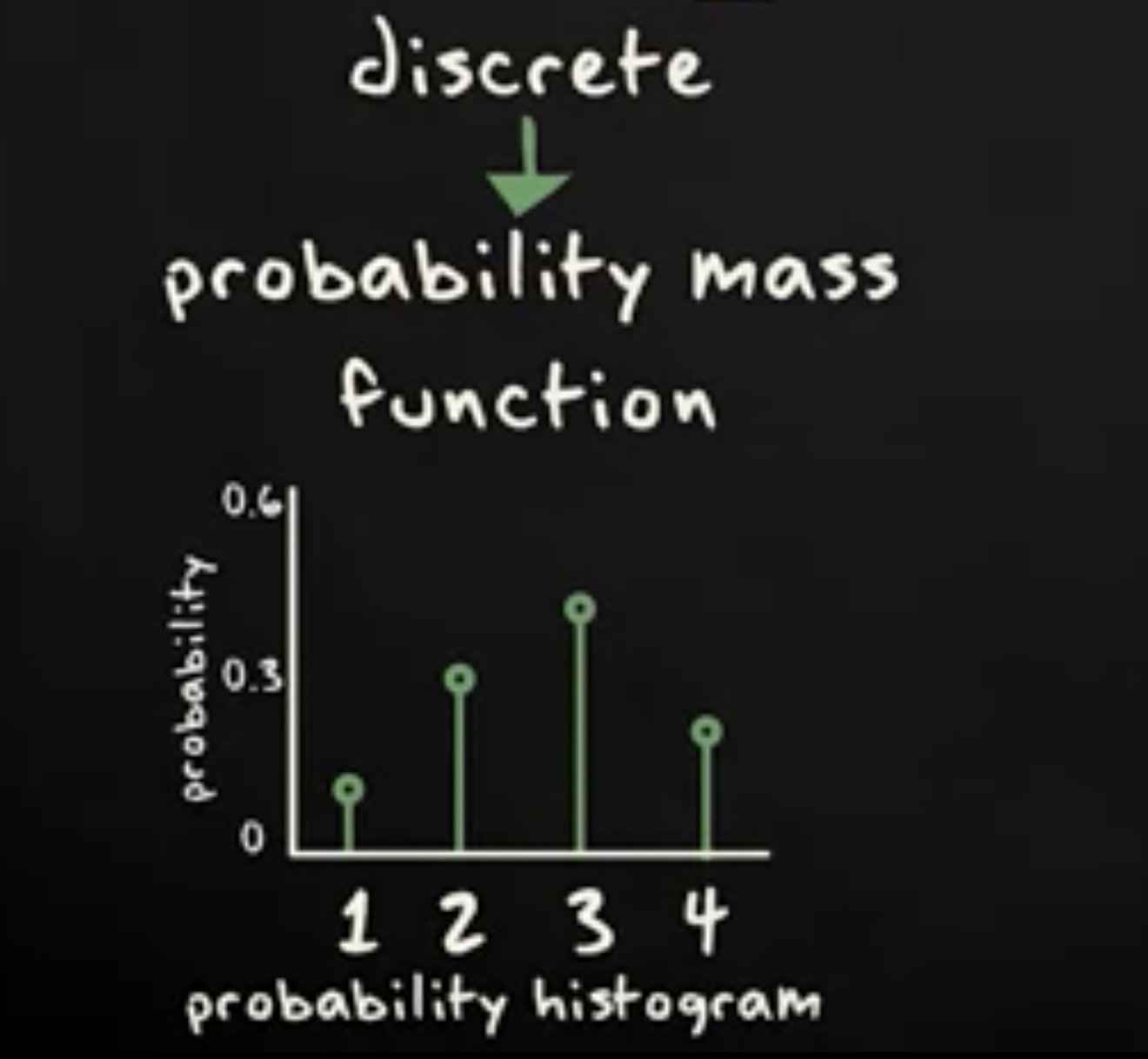
根据定义,每个随机变量都有一个概率分布,离散随机变量的概率分布叫 概率质量函数 ,而连续随机变量的概率分布叫概率密度函数。至于为什么有这种区别,稍后解释。
对于离散随机变量来说,通过列出每种可能的结果,容易看出概率。假设变量 X 接收 1, 2, 3, 或者 4 。那么下面这张表就列出了每种结果的概率。分布还可以用概率直方图来描述,这跟频率表或者频率直方图的用法如出一撤。
对于连续随机变量,可以采用图表。下图中的概率分布并没有在 y 轴上给出概率,而给出了 概率密度 (probability density) 。为了获得概率,你需要考虑曲线某个区间下方的区域而非曲线的高度。概率就是由这块区域的面积给出的。
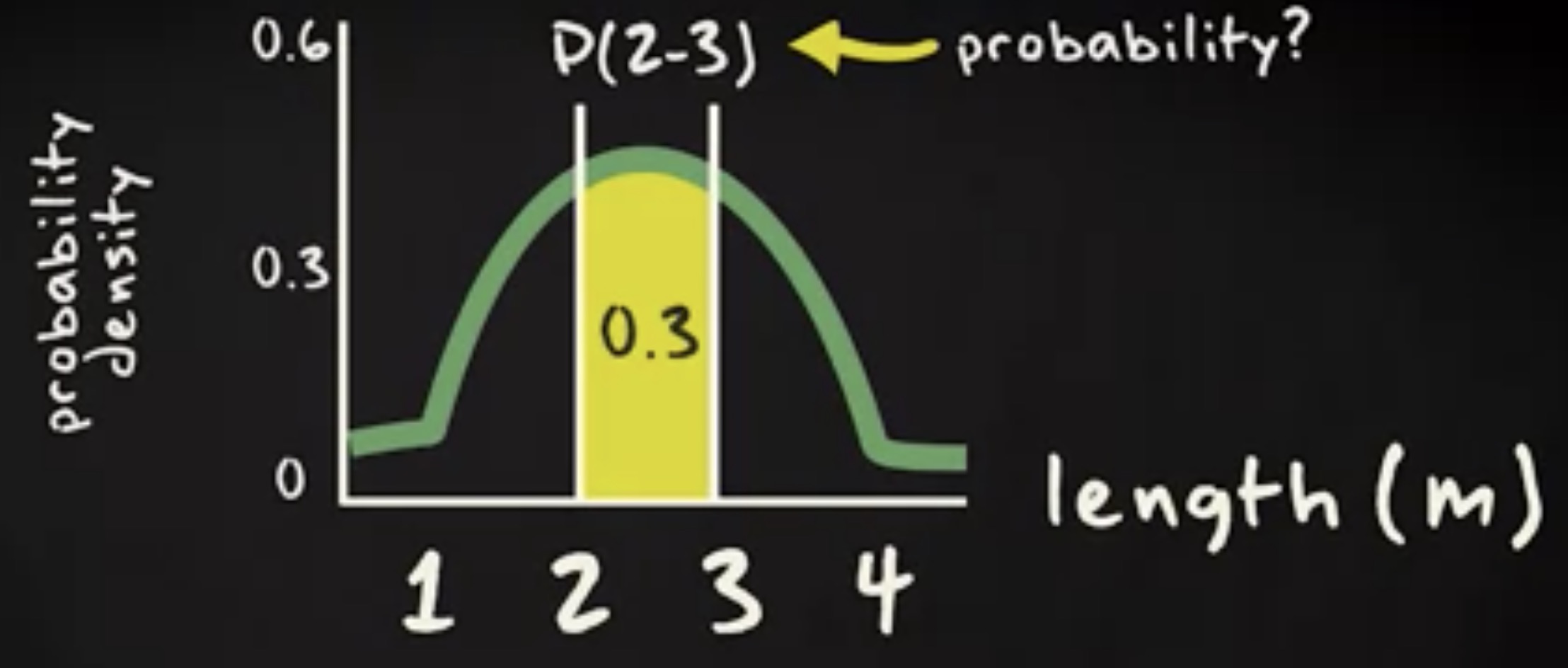
y 轴之所以要采用密度是因为你的随机变量单位可能会改变。比如,你表示的长度由米改成厘米,这个时候密度相应改变,而区域的面积不应该变化。
小结
- 随机变量是一个由随机现象产生多种可能结果的变量。当结果有限可数时,它是离散的;当结果数量无限时,它是连续的。
- 概率分布为随机变量可取得的每个值指定概率。离散随机变量的概率分布叫概率质量函数,而连续随机变量的概率分布叫概率密度函数,它的概率值时通过概率曲线指定区间下的面积来获得的。
- 概率密度函数可以以表格、图表或者方程的形式呈现。
累积概率分布
你已经了解了基本的概率规则,也了解了概率分布,是时候向你介绍累积概率分布了。
首先看看下面这个简单的离散随机分布。你能找出 X 的值是 2 或者 3 的概率吗?
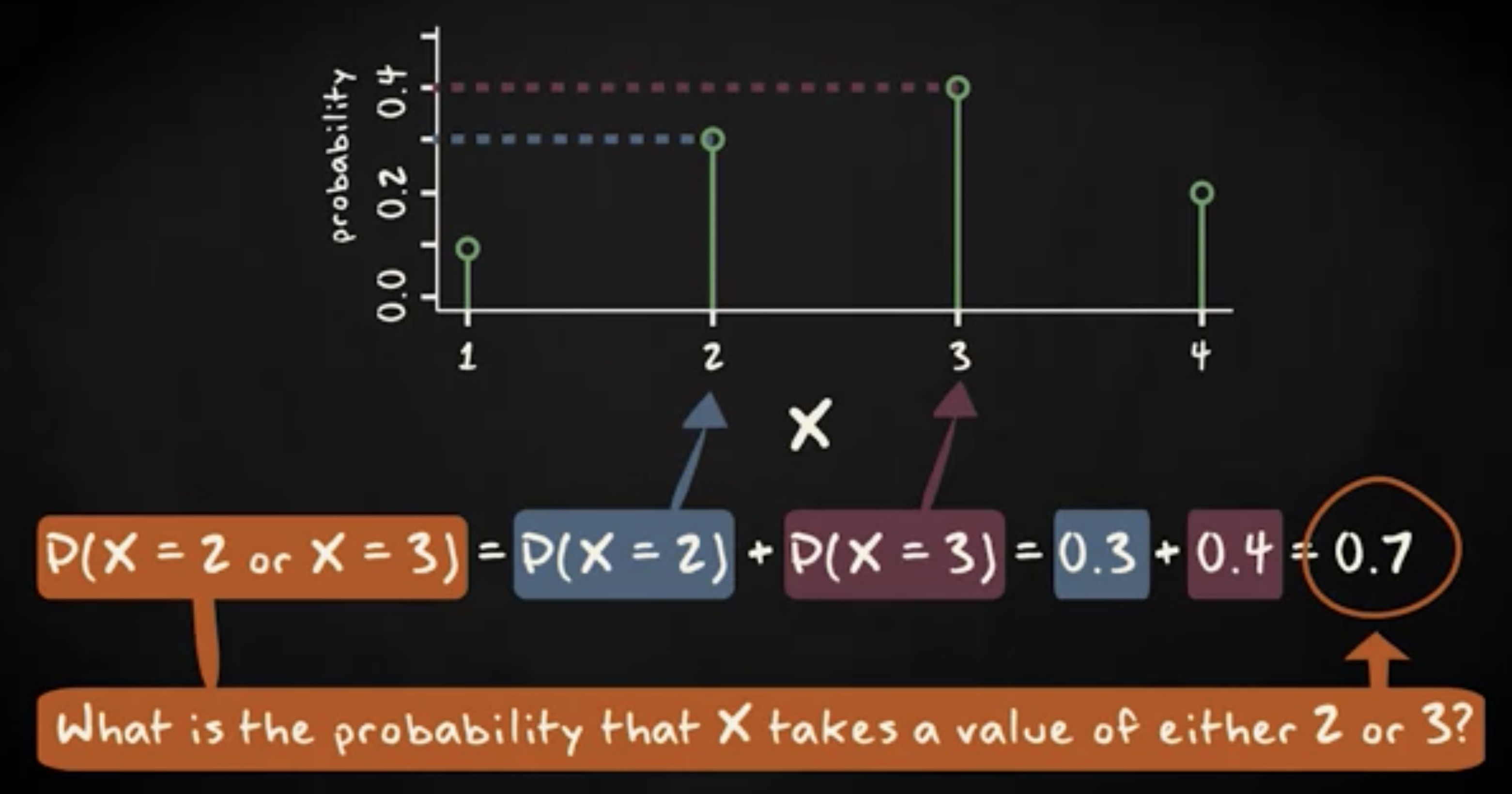
答案可以通过把 x 是 2 或者 x 是 3 的概率相加得到。因此这个值是 0.7 。
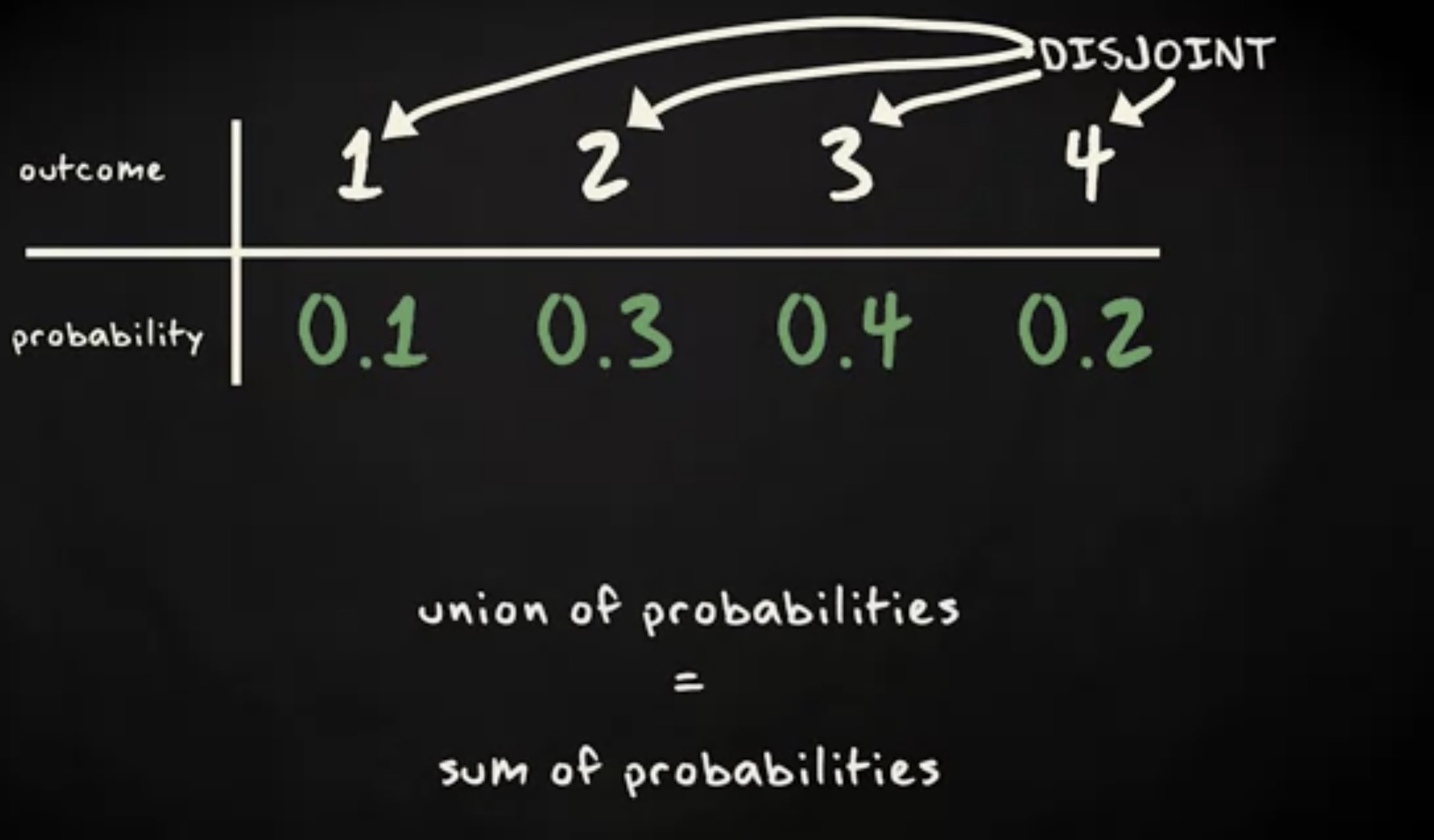
表格上列出的概率,或者说概率质量函数 x 轴上的概率,全部都是互斥。因此任意概率的并集实际上就是这些概率值之和。相似的,根据补集的规则, X 大于等于 1 的概率等于 1 减去 x 是 1 的概率,也就是 0.9 。

现在让我们往下接着走。基于概率分布,我们很容易计算出小于或者等于某个值的概率。举个例子, x
小于或者等于 1 的概率是 0.1 。 x 小于或者等于 2 的概率是 0.1 加上 0.3 ,也就是 0.4 。
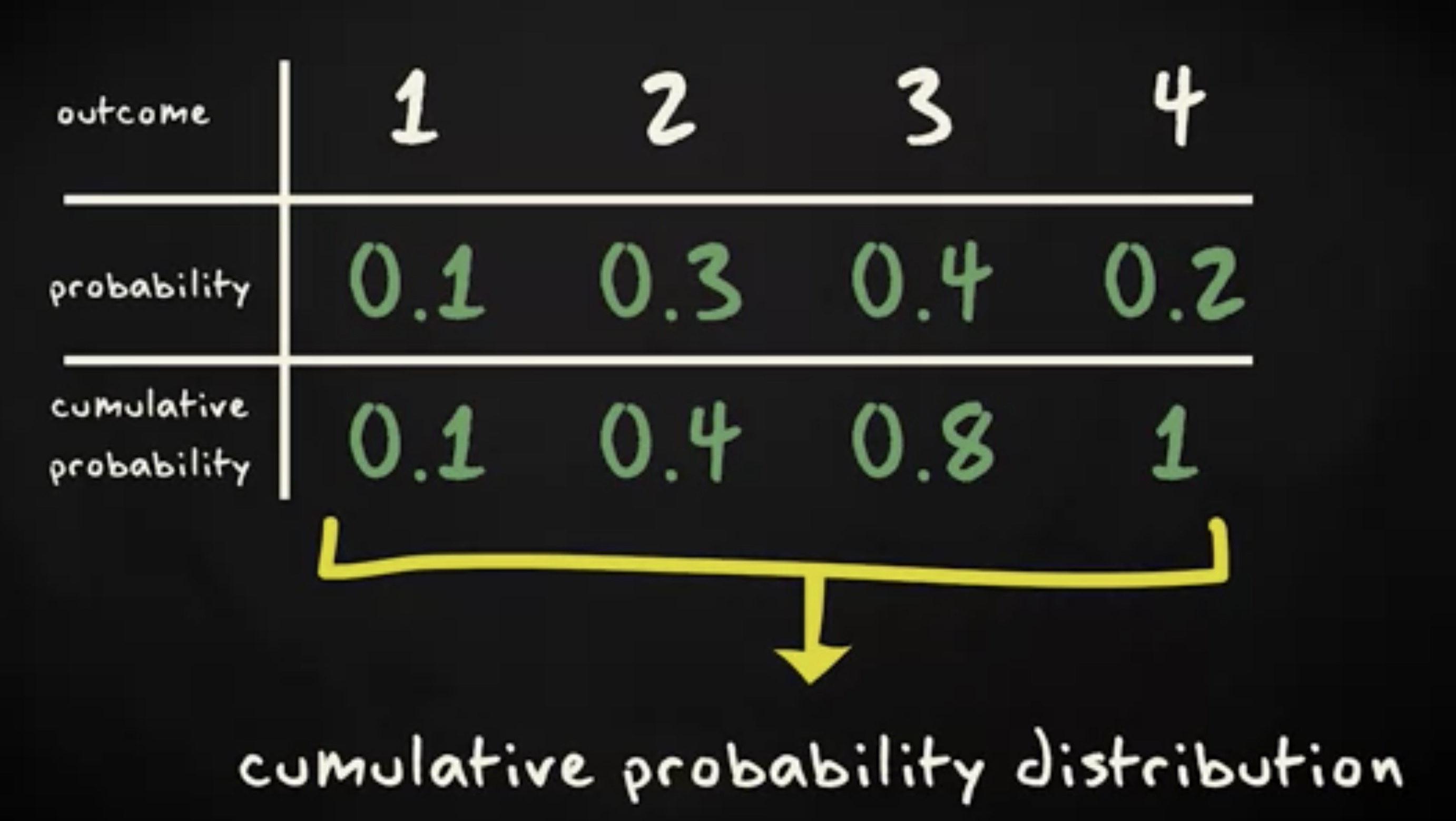
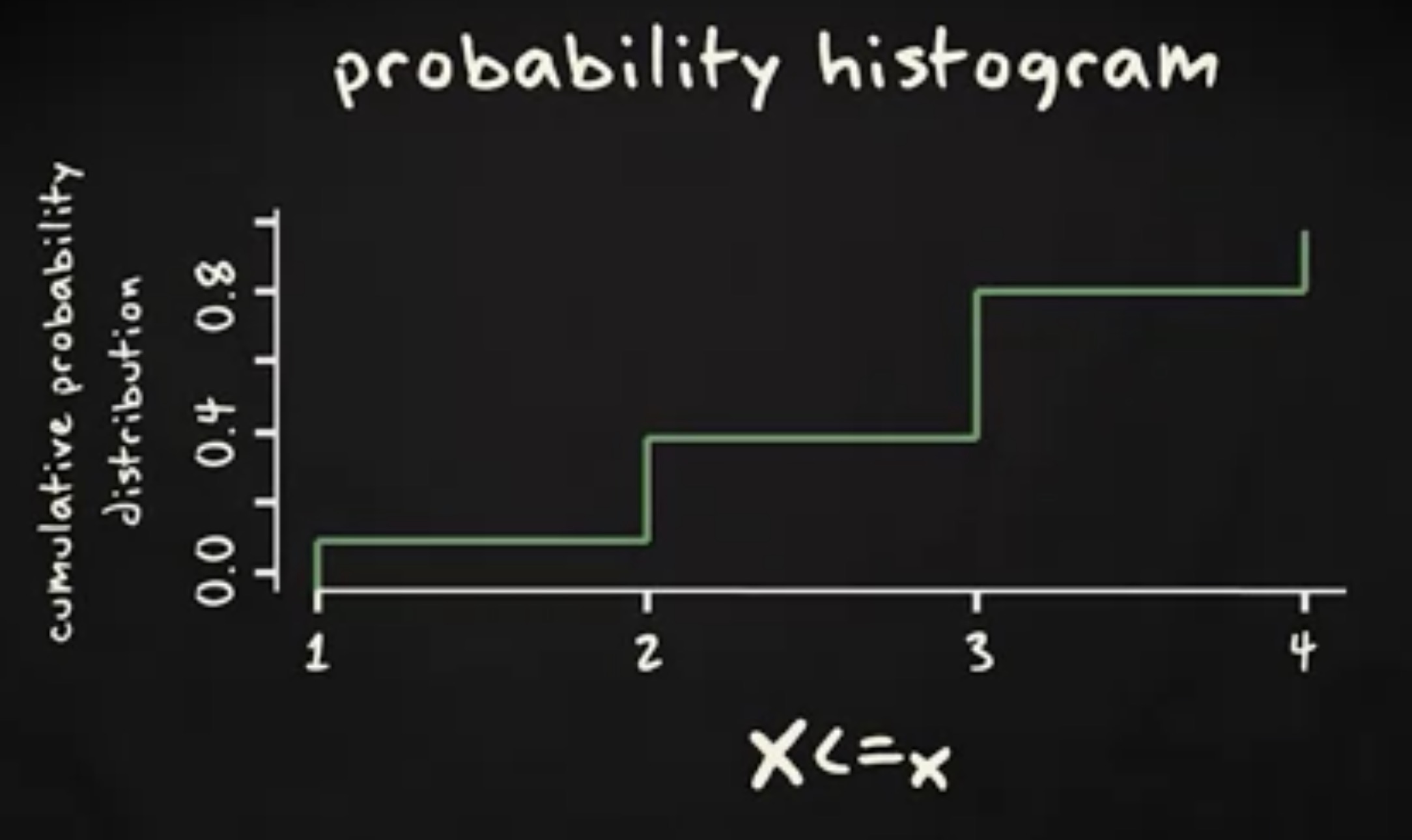
这种概率被称为 累积概率 (cumulative probability) 。 全部累积概率的列表被称为 累积概率分布 (cumulative probability distribution) ,或者 累积分布函数 (cumulative distribution function) 。这个累积概率分布的概率直方图可以像下面这样:
对于概率密度函数也是如此。例如,下面这个概率密度函数,对应旁边的累积分布。
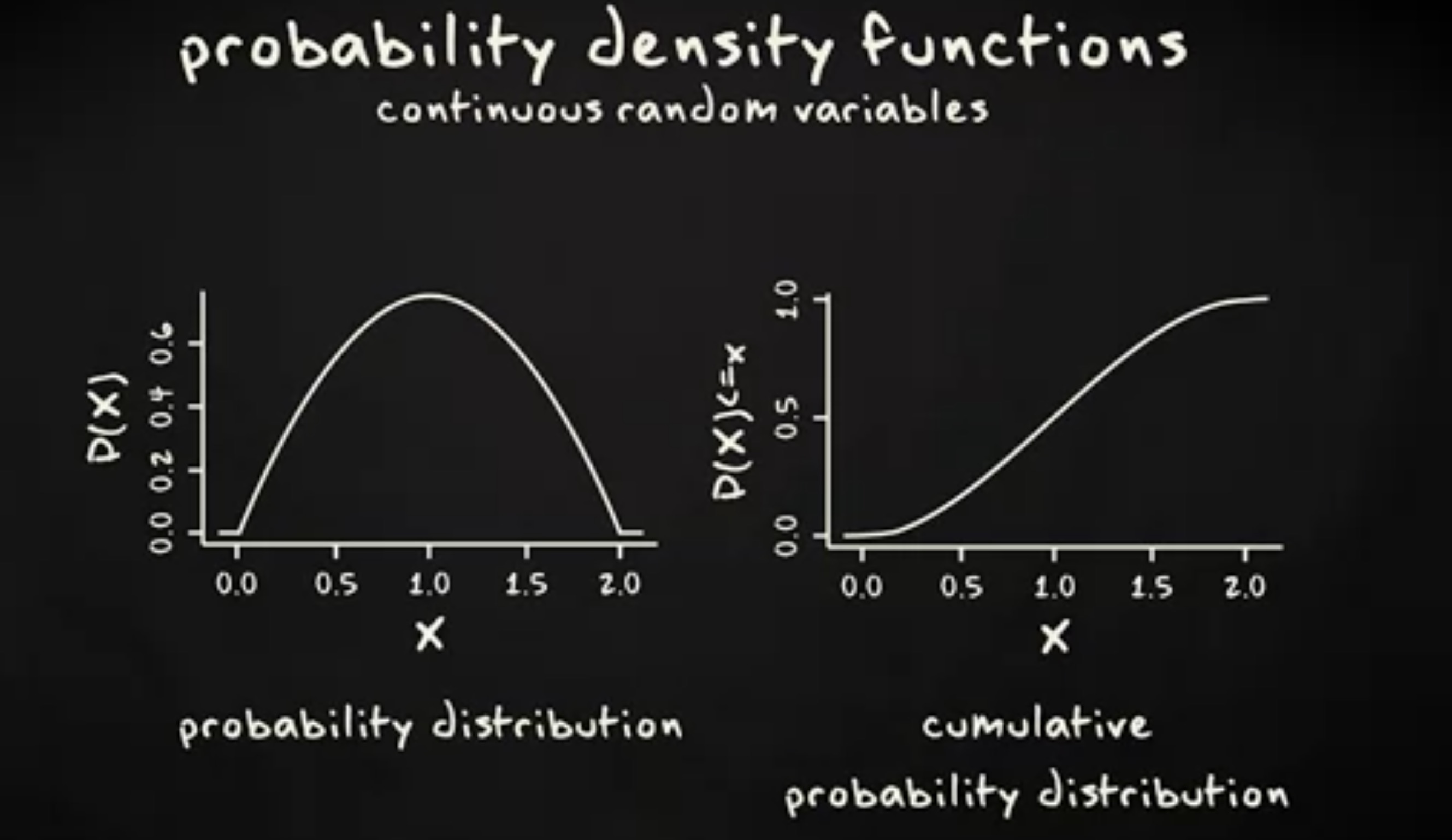
有趣的部分是, y 变量从概率密度变成了概率。
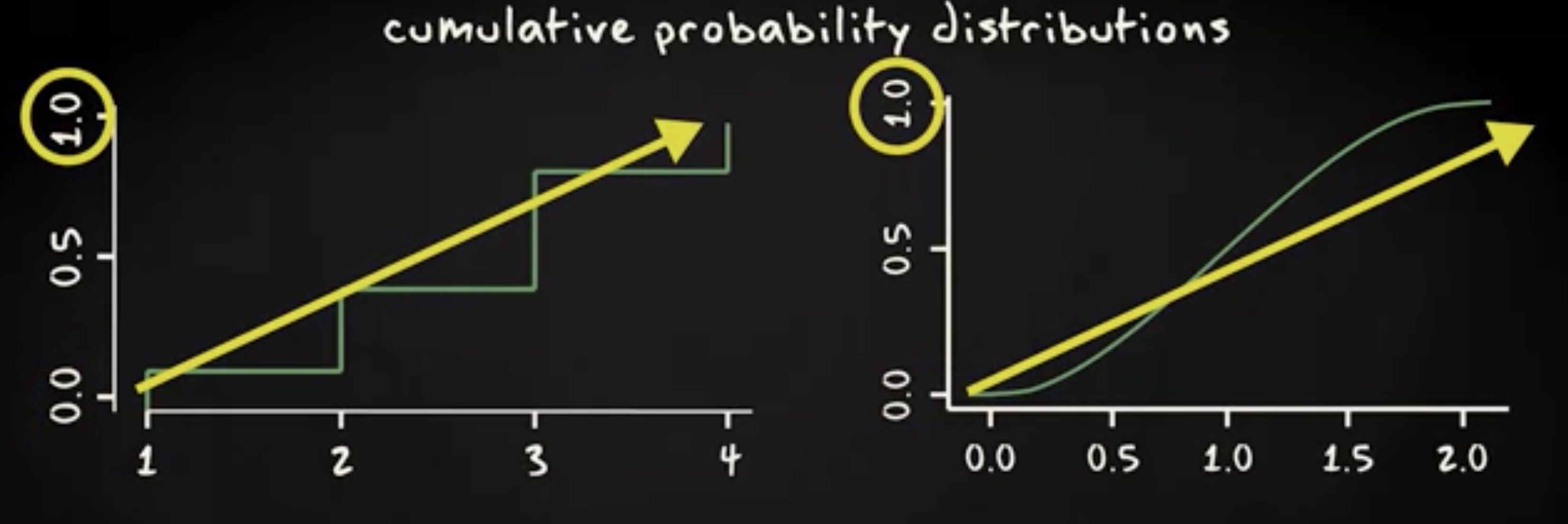
如你所见,累积概率函数从 0 开始,持续增加到最大值 1 。所有结果的概率之和等于 1 。累积分布,特别是它的图形化形式,十分便于回答两个问题。
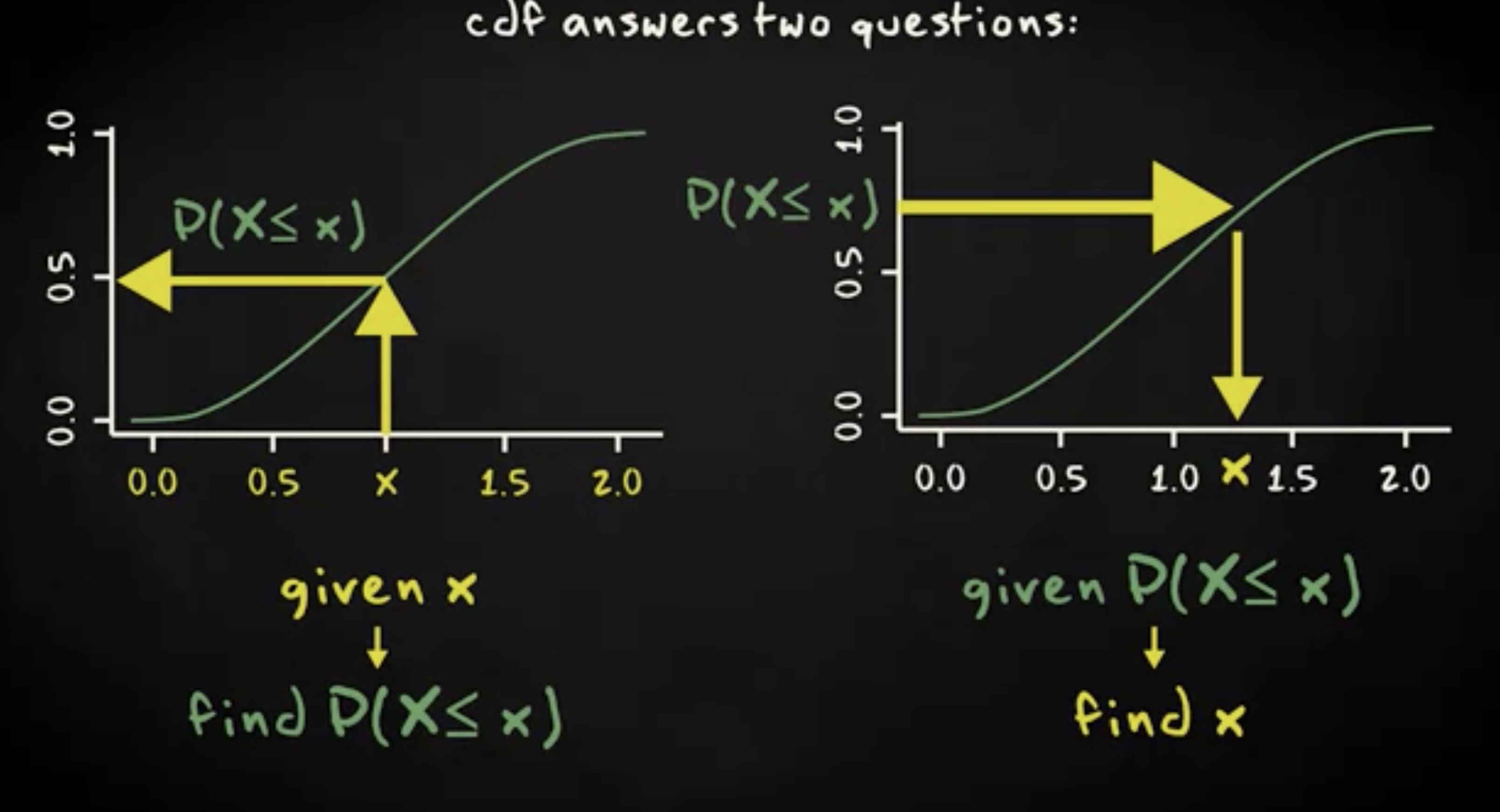
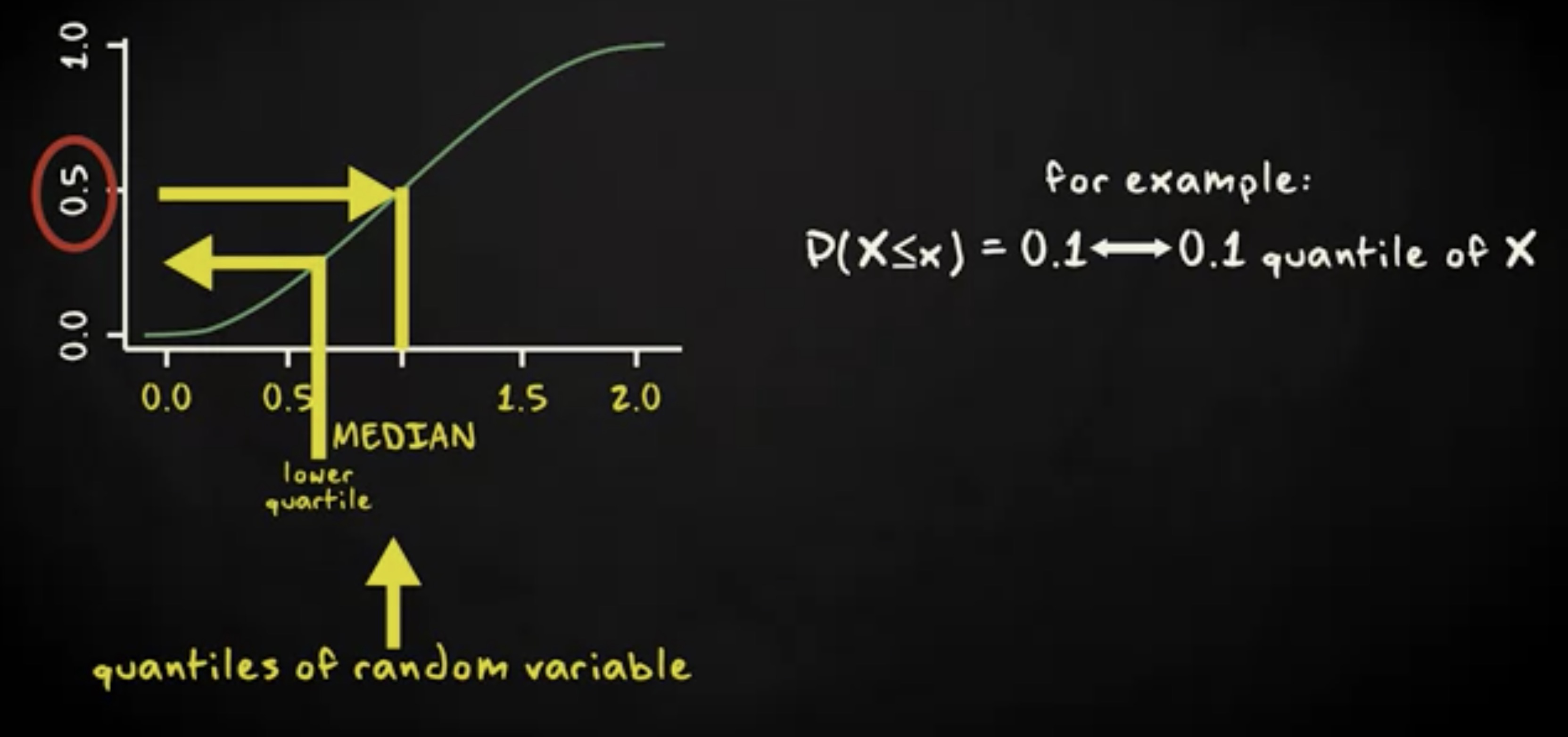
你可以在 x 轴上选择随机变量的某个值,然后在 y 轴上找到观察值的哪一部分小于或等于该值。或者相反,你可以在 y 轴上选择一个分数,然后在 x 轴上找到相应的阈值。对于这个阈值,有一个简短的叫法是 分位 (quantile) 。举个例子,对于累积概率 0.1 以下的阈值,就称为 0.1 分位。因此累积概率分布实际上展示了随机变量的分位。举个例子,你会发现,对于累积概率 0.5 ,你找到其实就是随机变量的中位数,对于累积概率 0.25 ,你找到是随机变量的四分位。
值得注意的是,对称概率分布下,中位数和平均数一致。
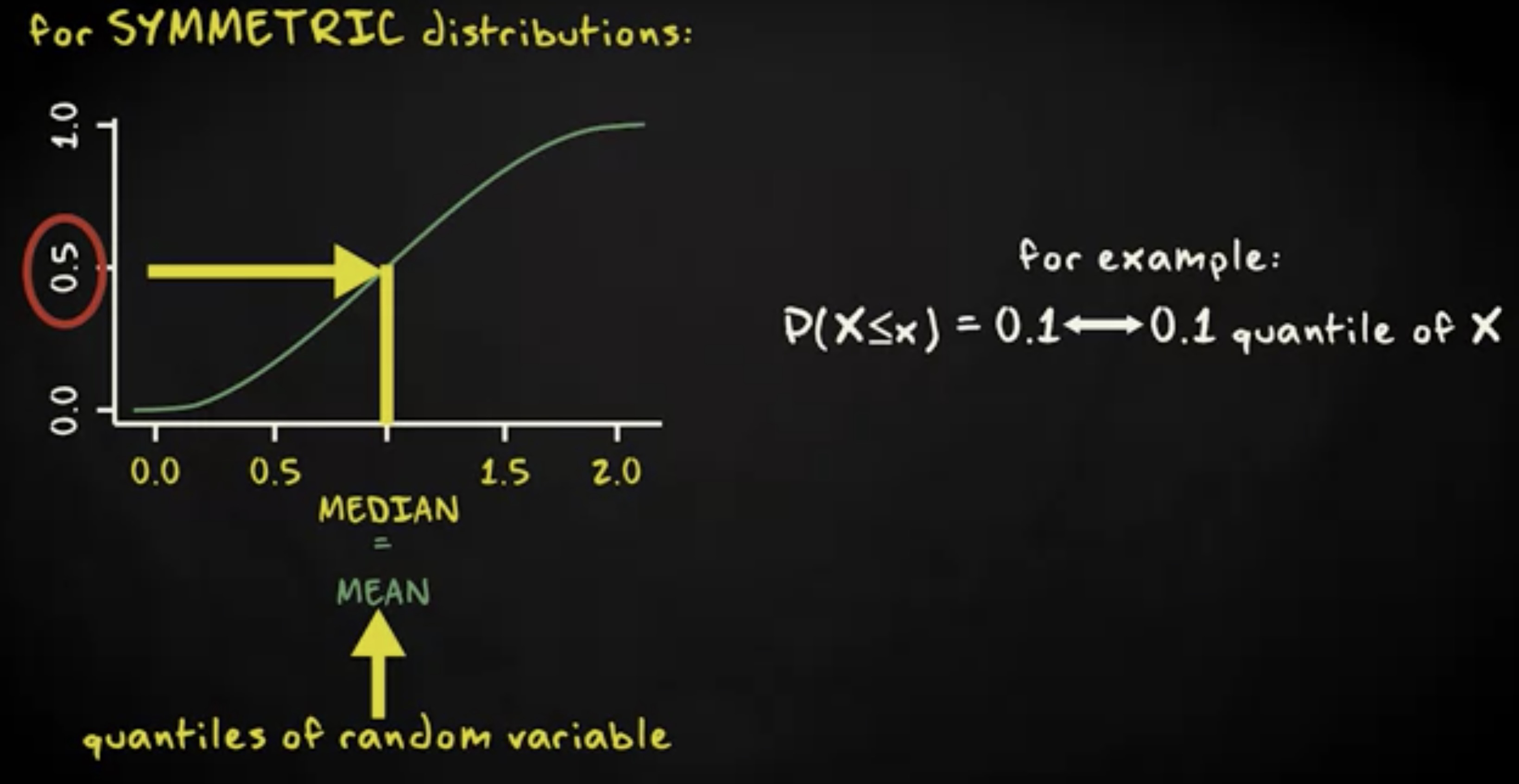
因此,对于对称分布,找到平均值的地方,累积概率也是 0.5 。
小结
- 随机变量的累积概率是获取一个小于或者等于某个阈值的概率。另一方面,累积概率体现了随机变量的分位。举个例子,累积概率 0.5 代表随机变量中位数被找到的地方。
- 跟概率分布一样,累积概率分布也可以以表格、图表或者方程的形式呈现,通过从小到大计算随机变量的概率实现。
- 随机变量从 0 持续增加到 1 。在对称概率分布下,中位数和平均数一致。

