欢迎关注微信公众号「Swift 花园」

样本空间 (sample space)

海滩是一个多变的环境 —— 尤其当天气很好的时候，有许多人，需要可以做的事情和可以看的风景。这一节教程里，海滩是我们的背景。我将向你解释几个可以帮助我们找到概率的概念，以及一个可视化的辅助工具 —— 树形图 (tree diagram) 。

这是一个温暖的下午，你可以来点下午茶。幸运的是，你所在的海滩上，有一个卖下午茶的摊位。不过，茶点几乎快卖完了，只剩下一种类型的冰淇淋和两瓶软饮料。

有点不走运的是，有三个人排在你前面。不过还有个好消息是，摊主只卖给每个顾客一件东西。由于你实在很渴望喝到眼前这冰爽的饮料，你不禁开始寻思，“我喝到饮料的机会有多大呢？”

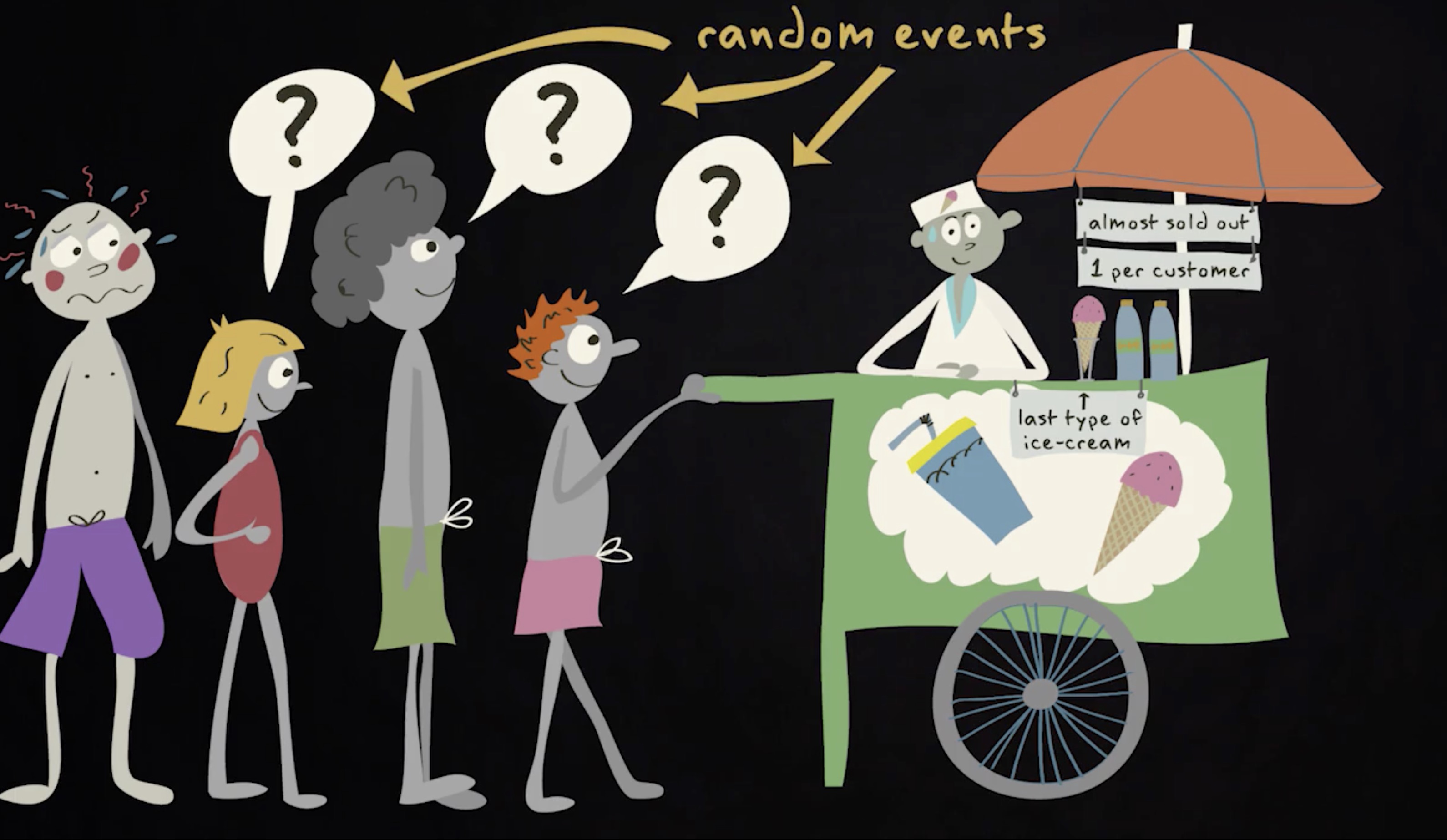
注意，你并不清楚其他顾客会做出的决定，所以他们的购买对你来说全部都是随机事件。第一个顾客可能买饮料或者冰淇淋，在这件事发生之后，第二个顾客拥有同样的选项，然后轮到第三个顾客。如果前面的两位顾客都买了饮料，那她就只剩冰淇淋可以选，否则的话，她也还有两个选项。

通过下面这幅树形图，你排序了所有可能的随机试验结果。看起来有 7 种可能的组合。这里所有随机现象的里列表我们称为 样本空间 (sample space) 。

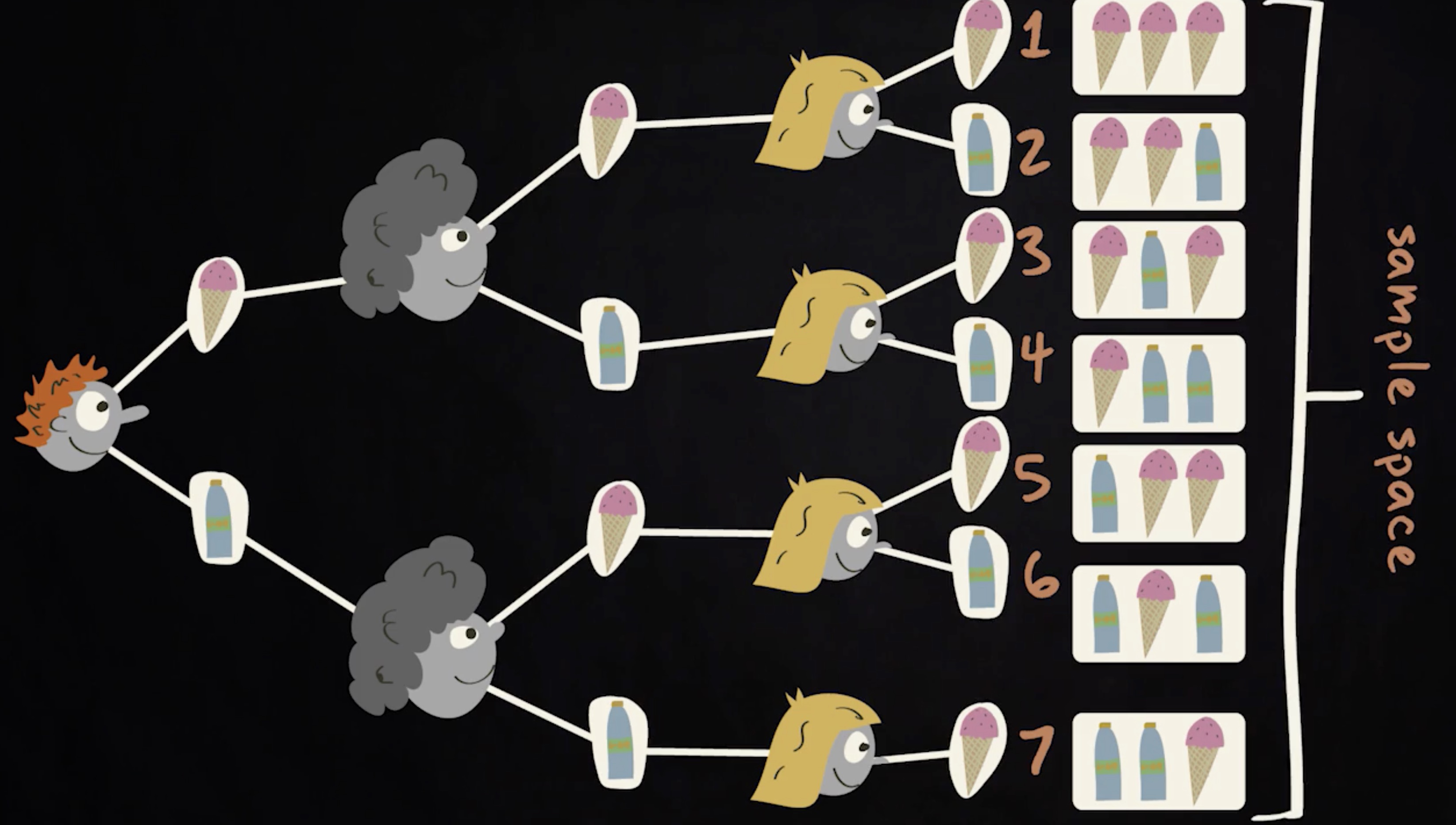
如果一个随机试验有离散的结果，比如我们的这个案例，一种描绘样本空间的便捷方式是通过树形图列出所有的可能性。就像上图中我们已经做的那样。在一个树形图中，有一些中间结果的划分，跟最终分支如出一撤。任何结果，包括结果的组合，被称为 事件（event），因此， 一个事件其实就是一个样本空间的子集 。在这个特定的案例中，你关心的事件，不走运的那些 —— 没有饮料喝了，反之，还能买到饮料。

任何一个随机事件都有与之关联的概率，并且小的事件可以组合成大的事件。量化这些事件的概率，可以通过实验。实验可以包含在一段足够长的时间内，观察冰淇淋和饮料的销售情况。但这里时间不够，当第一个顾客正在思考要买什么的时候，你就必须做出自己的决定了。于是你诉诸另外一种策略 —— 对样本空间里的结果做出有说服力的假设。

你假定每一种事件发生的机会相等 —— 每个顾客选冰淇淋和饮料的概率都是 0.5 。在这种方式中，你可以依赖通用的概率规则。概率处于 0 到 1 之间，所有可能的结果，例如，所有选项在树形图里以节点表示，它们最终的总和也等于 1 。借助它们，你可以很快得到答案。这个答案可能帮助你做出决定：是应该保持乐观，在队伍中等着轮到自己，还是应该开始考虑寻求别的方式购买饮料。

不过，要记得，经过所有事件都已经展开，你并不知道你对于概率的评估是否正确。虽然你收集了排在你前面的三个顾客的试验信息，但对于整个购买冰淇淋和饮料这种事情来说。你的信息极其有限，并没有办法推导出十分精确的概率估算。

小结

样本空间是所有随机现象的结果的集合，而事件是样本空间的子集，它对应某一个随机变量的结果或者一组可能的结果。
每个事件都有概率。为了找到这些概率，你可以用到树形图。在树形图中，你可以创建样本空间，并对各种事件显式地做出假设。为了量化树形图里每个事件的概率，你可以进行实验。
某些时候，你可以对样本空间里的结果做出有说服力的假设，然后基于推理估计出它们的概率。
在任何案例中，通用的概率规则都适用于树形图。任意事件的概率都处于 0 和 1 之间，而最终所有可能的结果的概率总和等于 1 。

用树形图量化概率

当你在思考随机现象并且把注意力放在事件之间的关系以及它们在树形图中的概率时，你已经开始计算概率和评估某件事发生的可能性。

下面我会解释实践中树形图中的概率是如何量化的。还是上面那个例子。下面这张图显示，你假定每个顾客都有 0.5 的概率选择冰淇林或者饮料。通用概率规则适用于树形图里的每一个节点。具体来说，如果你观察图中的第一个顾客，有两个分支，每个分支 0.5 的概率。到第二个顾客，有两对分支，每对占 0.5 的概率，一对里的两个分支又各占 0.5 的概率。

如果这个时候轮到你了，你需要沿着一条路径，从第一个顾客的某个购买结果算到第二个顾客的某个购买结果。在树形图中，通过计算这条路径上所有概率的乘积来找出最终组合的事件的概率。

两个顾客之后，你还有多大的机会买到饮料呢？至少得剩一瓶饮料吧，满足这个情况的事件分支有三条，像图示中那样，总的概率是 0.75 。

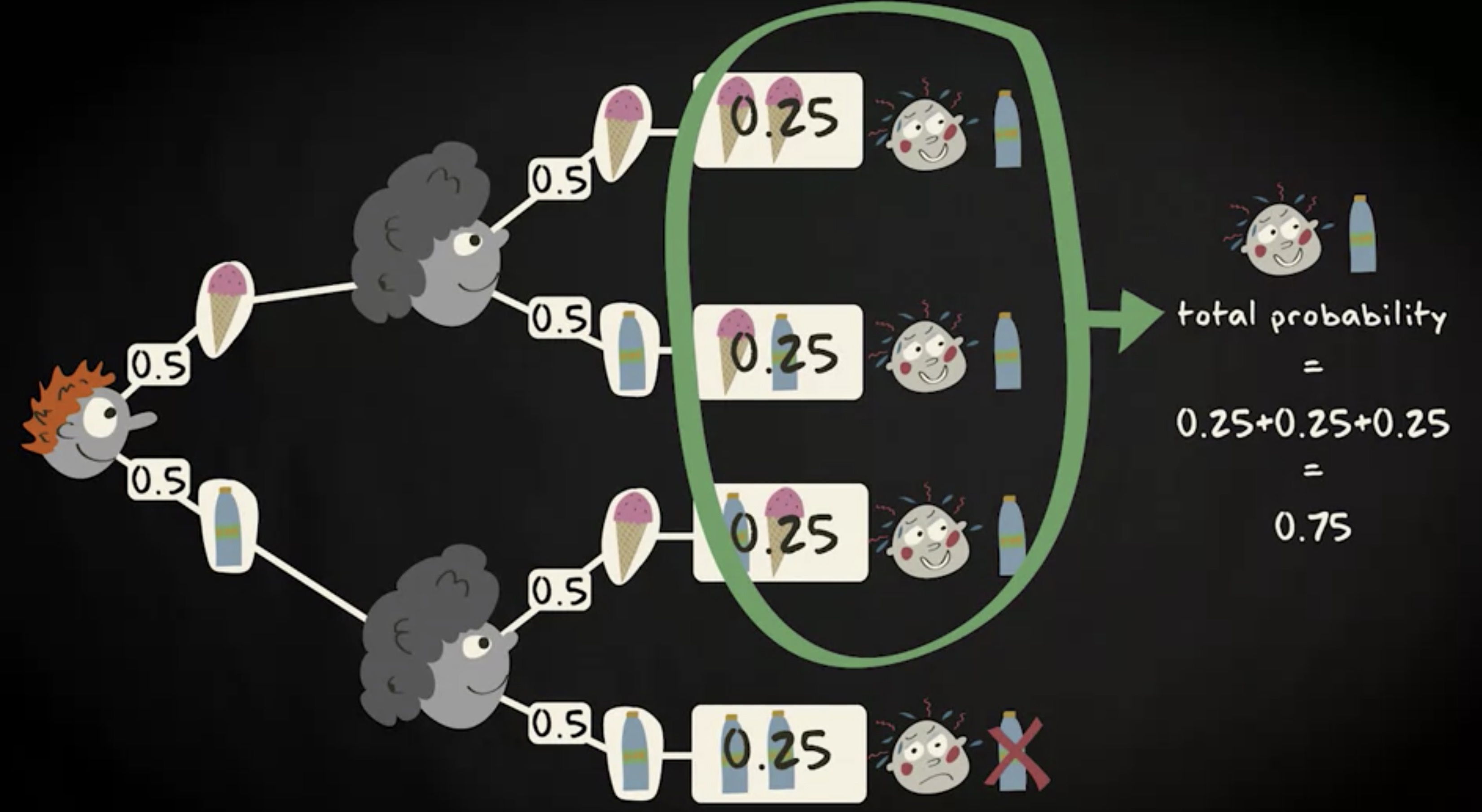
还有没有更快的算法呢？—— 利用所有概率的总和等于 1 这个规则。所以 1 减去两瓶饮料都卖出去的概率会给到我们相同的答案。

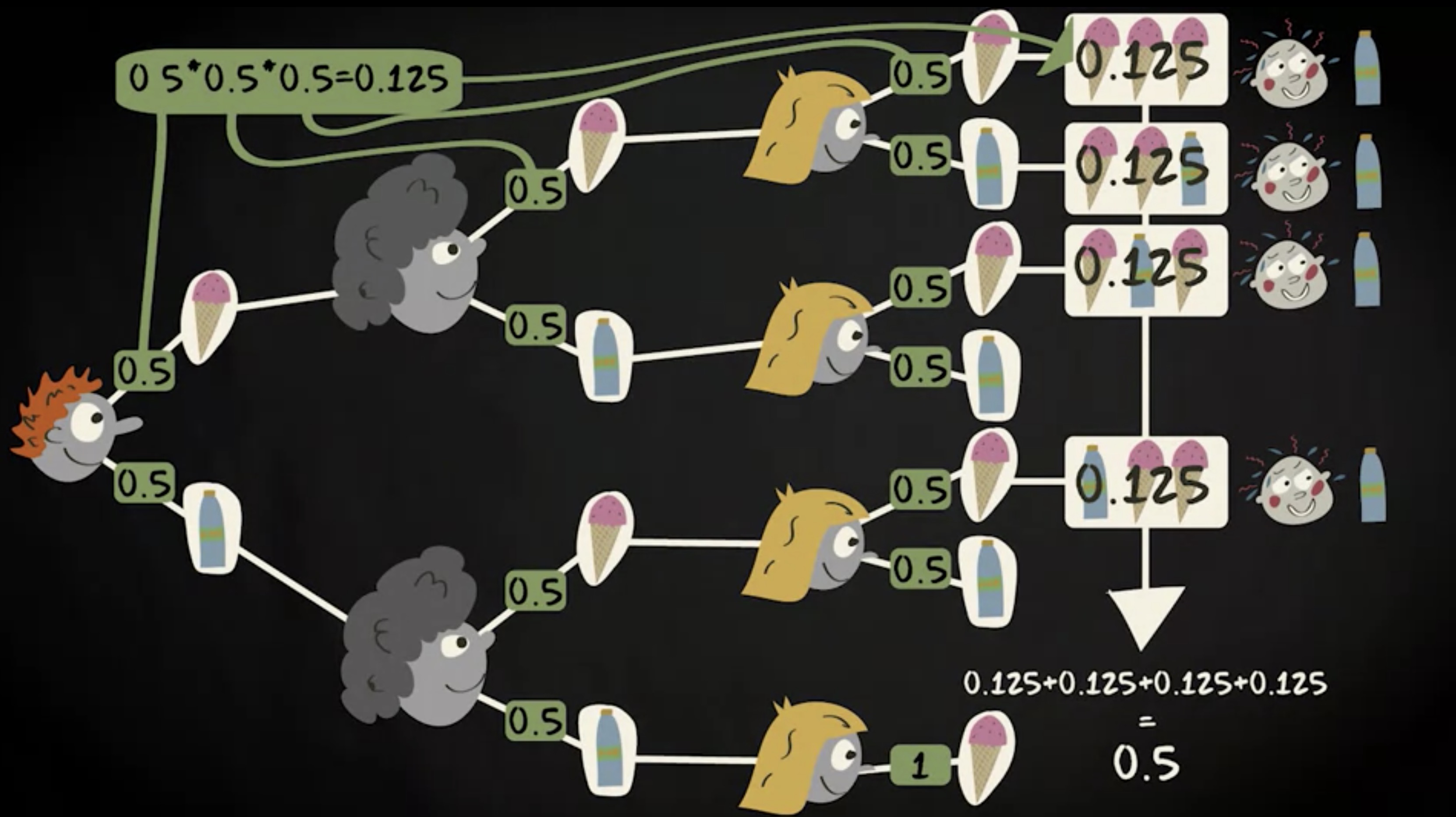
现在我们加大难度，考虑第三个顾客了。这里有一点特殊。她在四个分支中有三个拥有两个选项，但在两瓶饮料都卖完的这个分支上，只有一个选项 —— 买冰淇淋。同时在这里，规则也需要被满足，即所有概率的总和等于 1 ，所以这个单分支的概率就等于 1 。

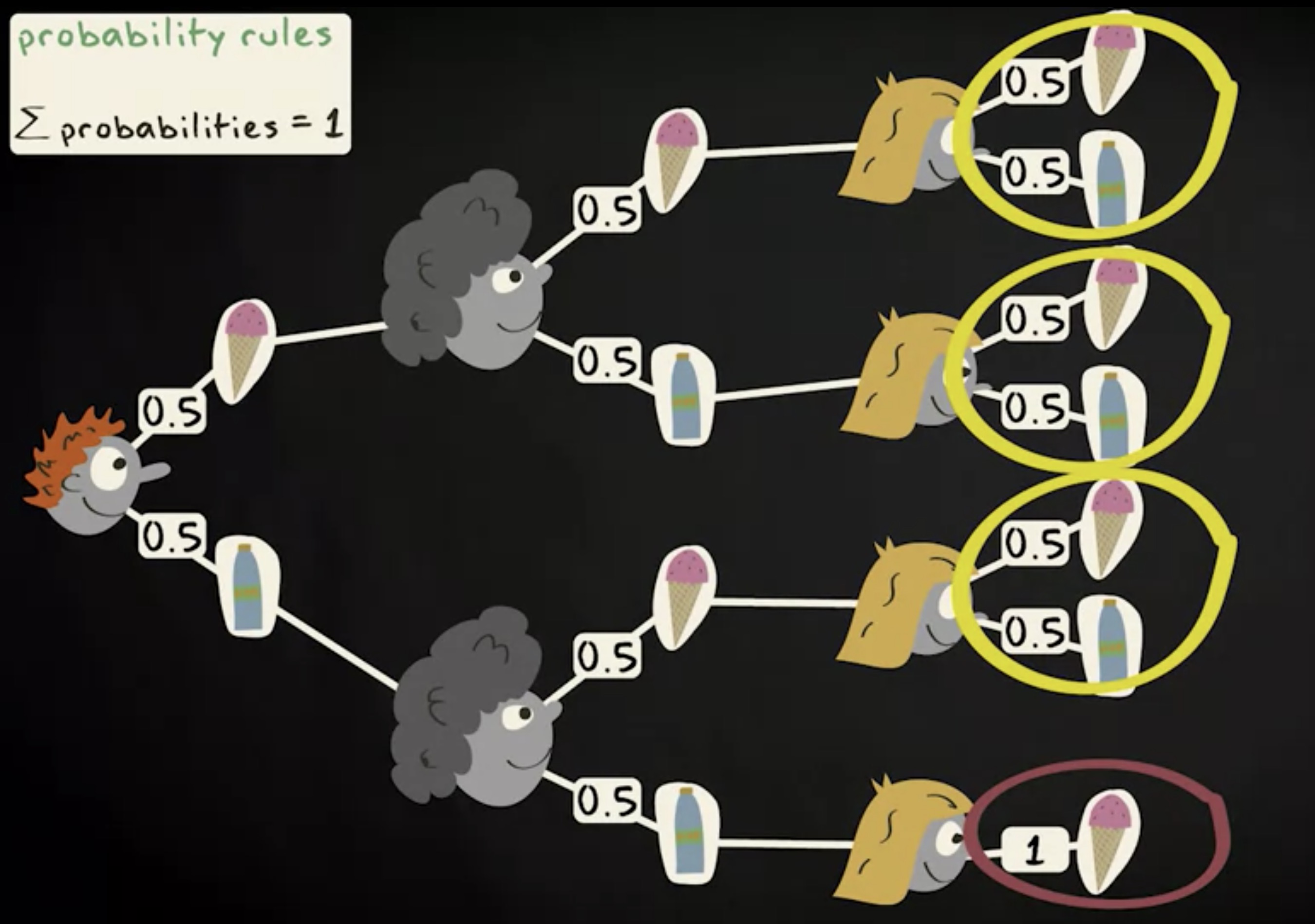
现在我们回到你买到饮料的机会上。我们需要算出四条分支的概率总和，即轮到你之前最多一瓶饮料被卖掉的概率总和。每条分支的概率等于 0.5 的三次方，即 0.125 ，加起来是 0.5。

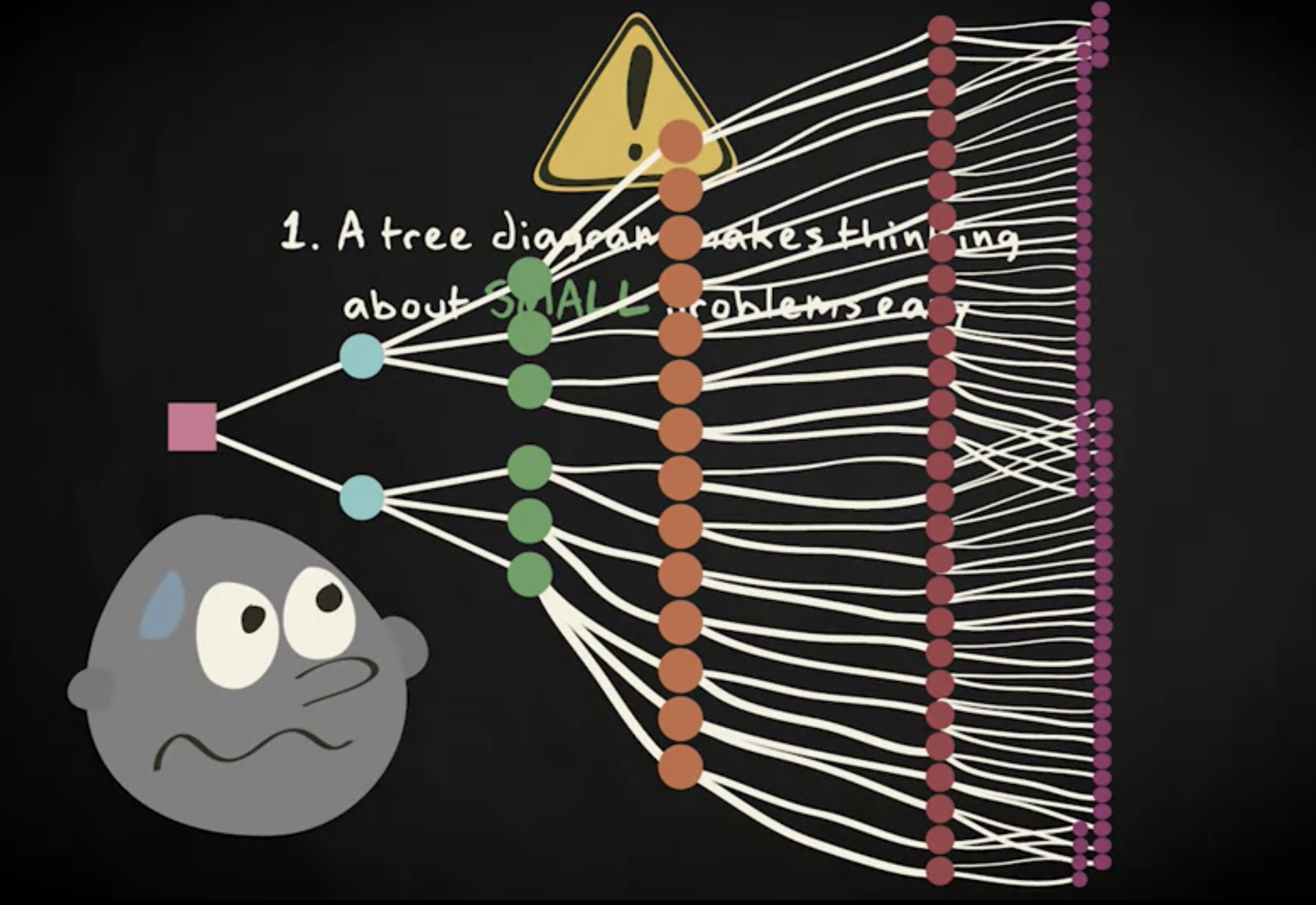
上面我们演示了利用树形图找出概率的变量，但也有必要指出一些需要注意的事情。首先是树形图可以很从容地处理小问题，对于理解有很多结果的随机现象，它并不是很适合 —— 它会变得很庞大，无助于保持概览。

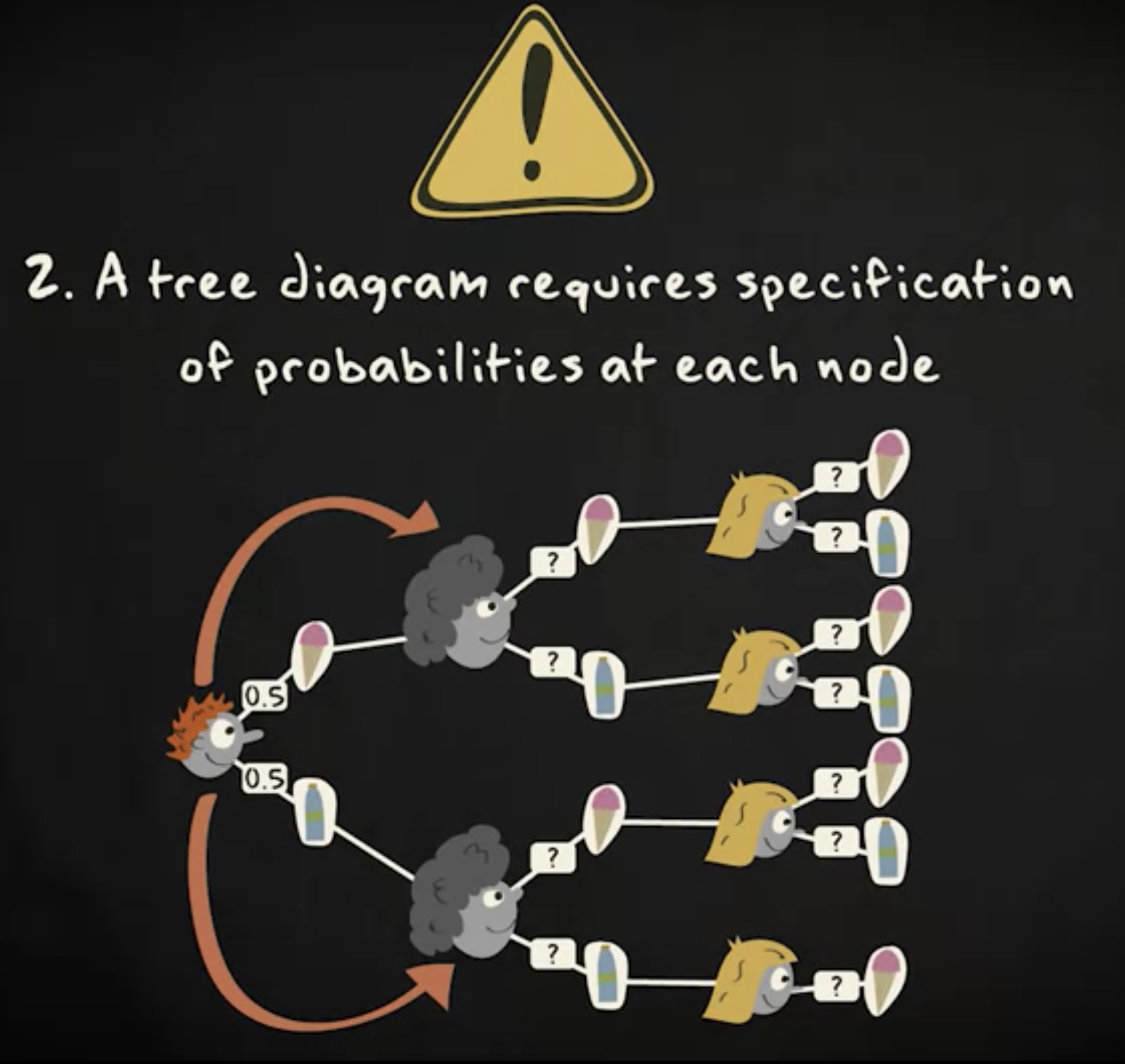
其次，为了实际应用树形图来量化概率，需要每个节点的概率规格。这在有的时候是很容易的，比如你假定每个选项机会均等，并且独立于前面的选择。另一方面，它也可能很困难。

举个例子，假如第二个顾客的购买选择会受到第一个顾客的影响怎么办呢？

小结

在树形图中，你可以创建样本空间，并对各种事件显式做出假定，包括每个事件的概率，它们在序列之中的相互独立性。
你可以在树形图中计算组合事件的概率。为了计算沿着一系列分支的从起点到结果的概率，所有的概率需要相乘。而为了找到某个包含很多种结果的事件的概率，所有这些结果的概率则需要相加。