欢迎关注微信公众号「Swift 花园」
正态分布 (normal distribution) 的函数形式
在所有的概率分布中,有一个特别出众,我们经常遇到。它就是 正态分布 (normal distribution) 。
在本节中,我们会学习它的重要属性。正态分布又被称为 高斯分布 (gaussian distribution) 。它是对称的,钟形,以均值 μ 和 标准差 σ 为特征。分布的最高点是均值的位置,宽度则由标准差指定。均值 μ 和 标准差 σ 被称为正态分布的 参数 (parameters) 。
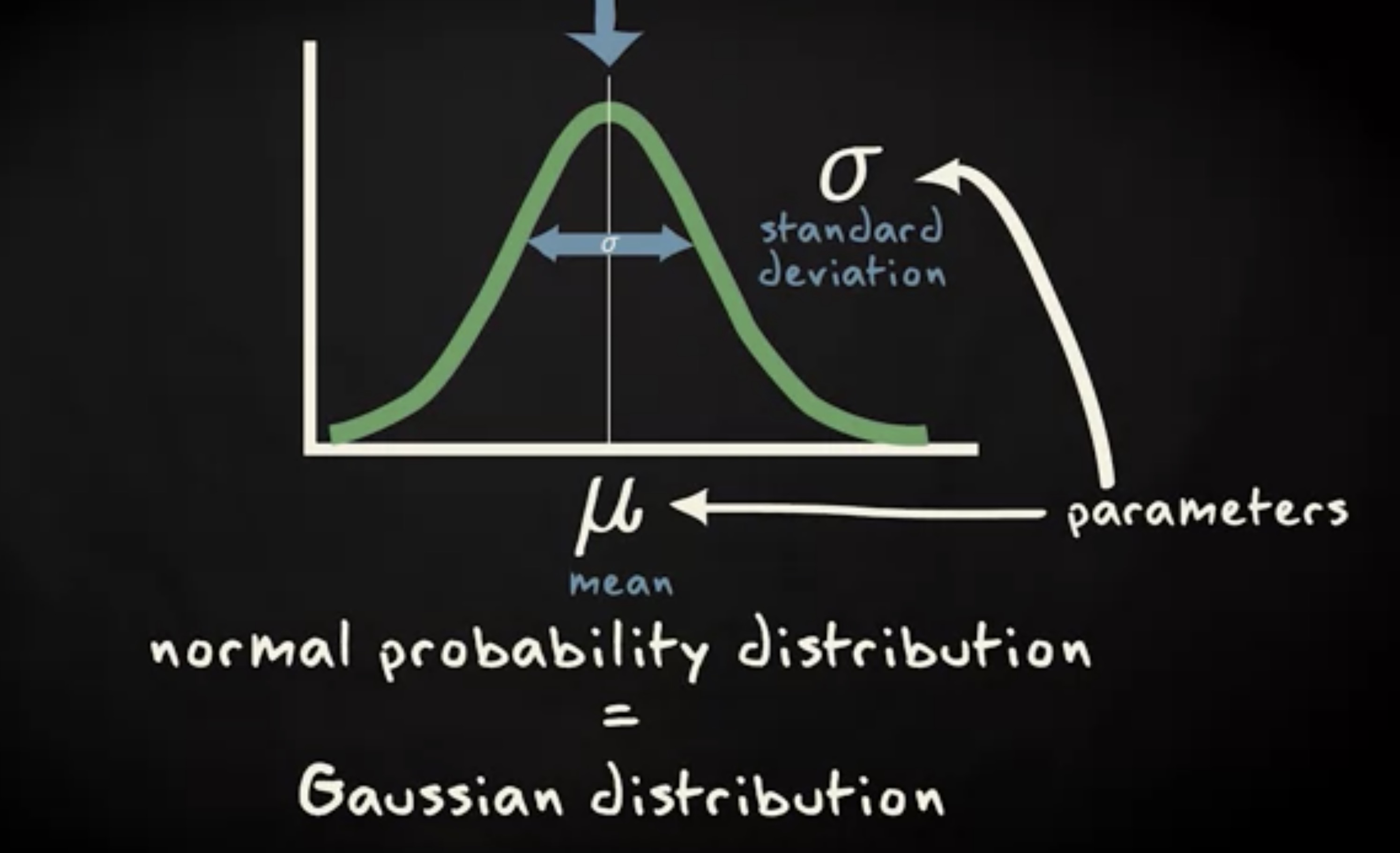
正态分布的累积概率分布是一个 S 函数曲线 (sigmoideal shape) ,均值处于概率为 0.5 的地方,标准差决定了曲线的陡峭程度。
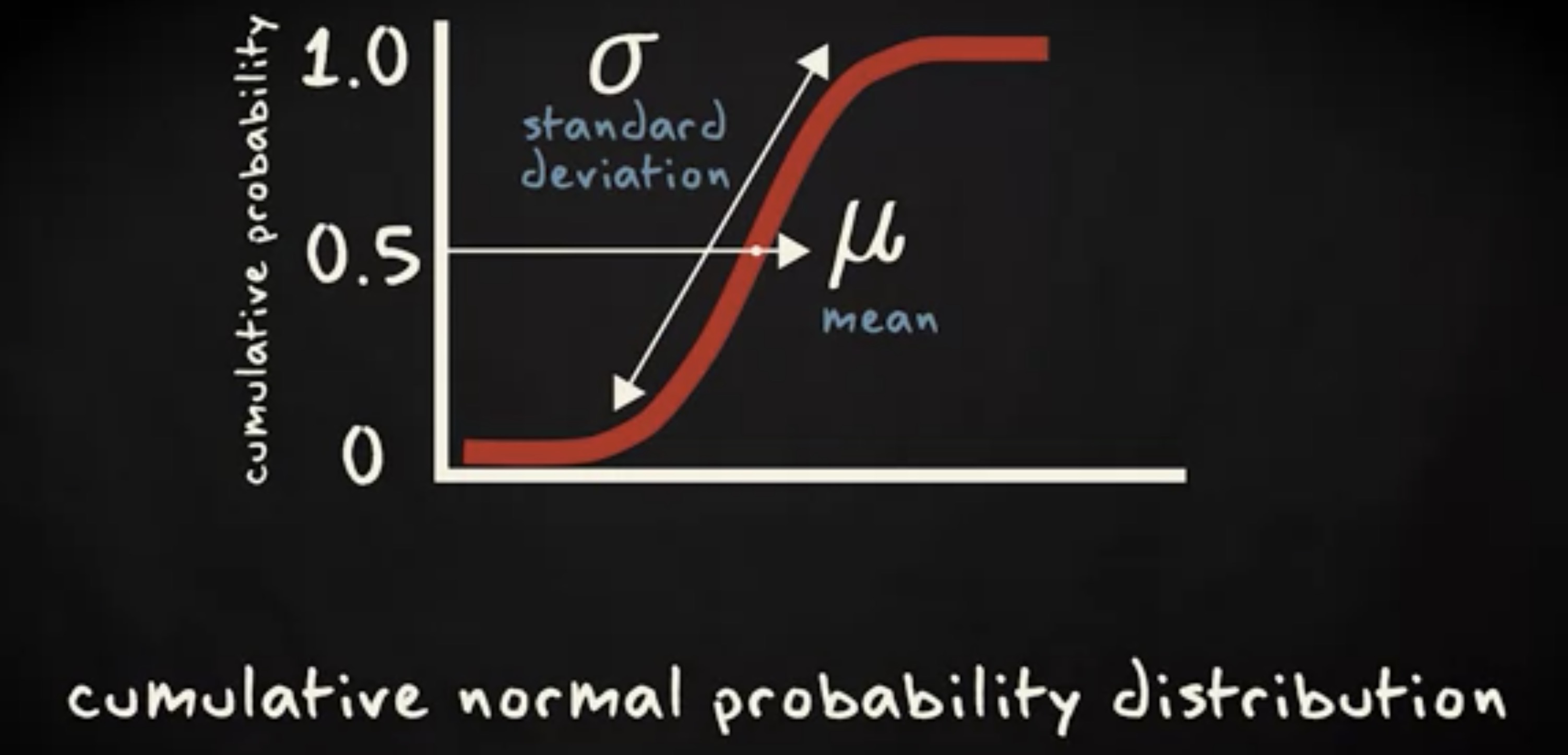
随机变量 X 有一个均值 μ ,标准差 σ 的正态分布,可以速记为:
而下面这个等式描述了完整的概率密度:
这个方程之所以重要,并非因为它第一眼看起来很复杂 —— 包含了三个重要的数学常量,$ \pi $,$ e $ 和 2 的平方根,还因为它连接了统计国王和物理世界。这个方程可以描述粒子扩散的过程。如果你释放一个扩散物,比如放一块糖到茶里,茶里的糖将按照这个方程的规律扩散。不仅流体是这样,大气中的颗粒物,道路交通,社会中的信息,都遵循这个分布的规律。
同时,我们会频繁地遇见高斯分布,是因为根据 中心极限定理 (central limit theorem) ,各种独立的随机过程组合之后,就会产出这种分布。不过,让我们不要跑题。我将通过拆解的方式来解释这个方程。
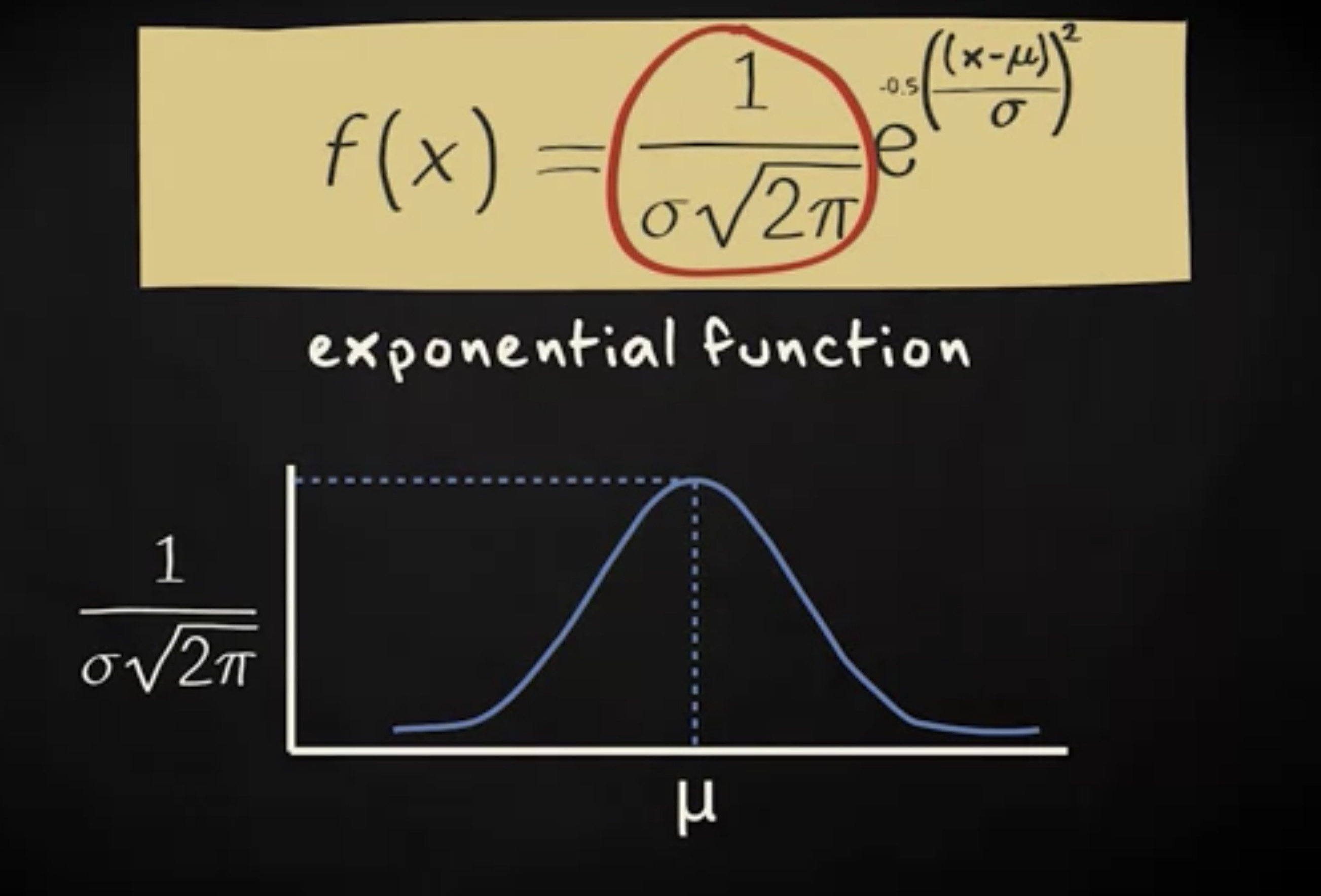
整个方程给出了随机变量 X 的概率密度,整个函数是一个 指数函数 (exponential function) ,前面是一个常数,然后指数部分包括小 x ,即随机变量可能取得的值。观察指数部分,从 x 中减去平均数,然后除以 σ ,这实际上是在计算 z 分数。所以随机变量的值在参与到方程后续的计算之前先做了标准化。

现在让我们聚焦到 e 之前的常数。在没有常数之前,曲线之下的面积是跟着 σ 变化的。但是通常乘以这个常量,这块面积变成了精确的 1 。这个常量的值实际上正是曲线顶部的高度,也就是 x 等于 μ 的地方。
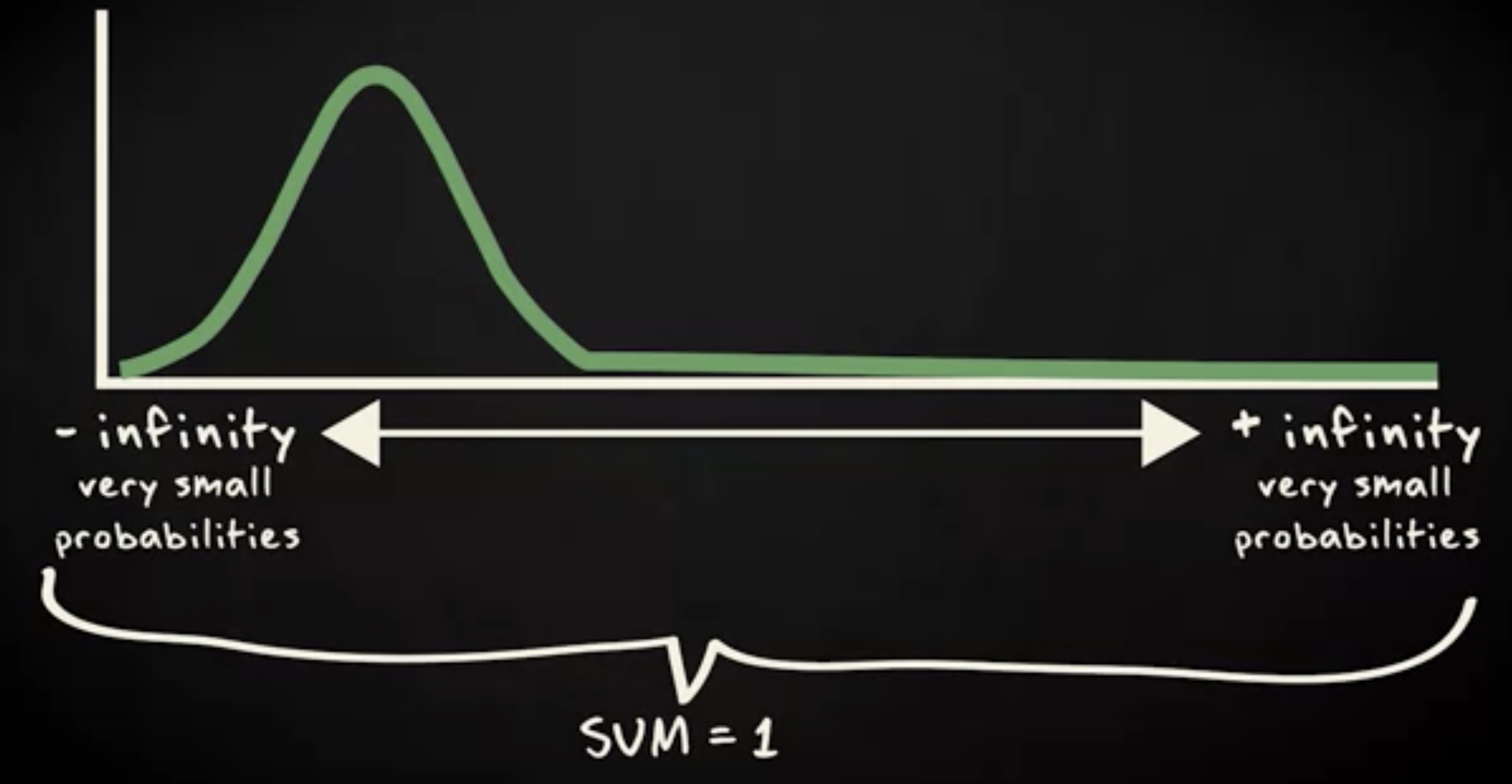
正态概率分布有一个违反直觉的属性 —— 当逼近极大或者极小的 x 时,概率接近于 0 ,但实际永远不可能是 0 。

这导致一个事实:随机变量的值可以往负无穷大和正无穷大无限伸展。即使这些值是极小的概率,但仍然满足所有概率之和等于 1 的规律。
最终确定之前,让我们回到 μ 和 σ 这两个参数,它们决定正态分布曲线的位置和形状。下图是一个西欧男性在一周中每天上班路上花的通勤时间。平均的通勤时间是 3 分钟,标准差 6 分钟,而同一个国家的西欧女性,通勤均值更小,但是标准差更大。你会发现,曲线越宽,顶点越低。
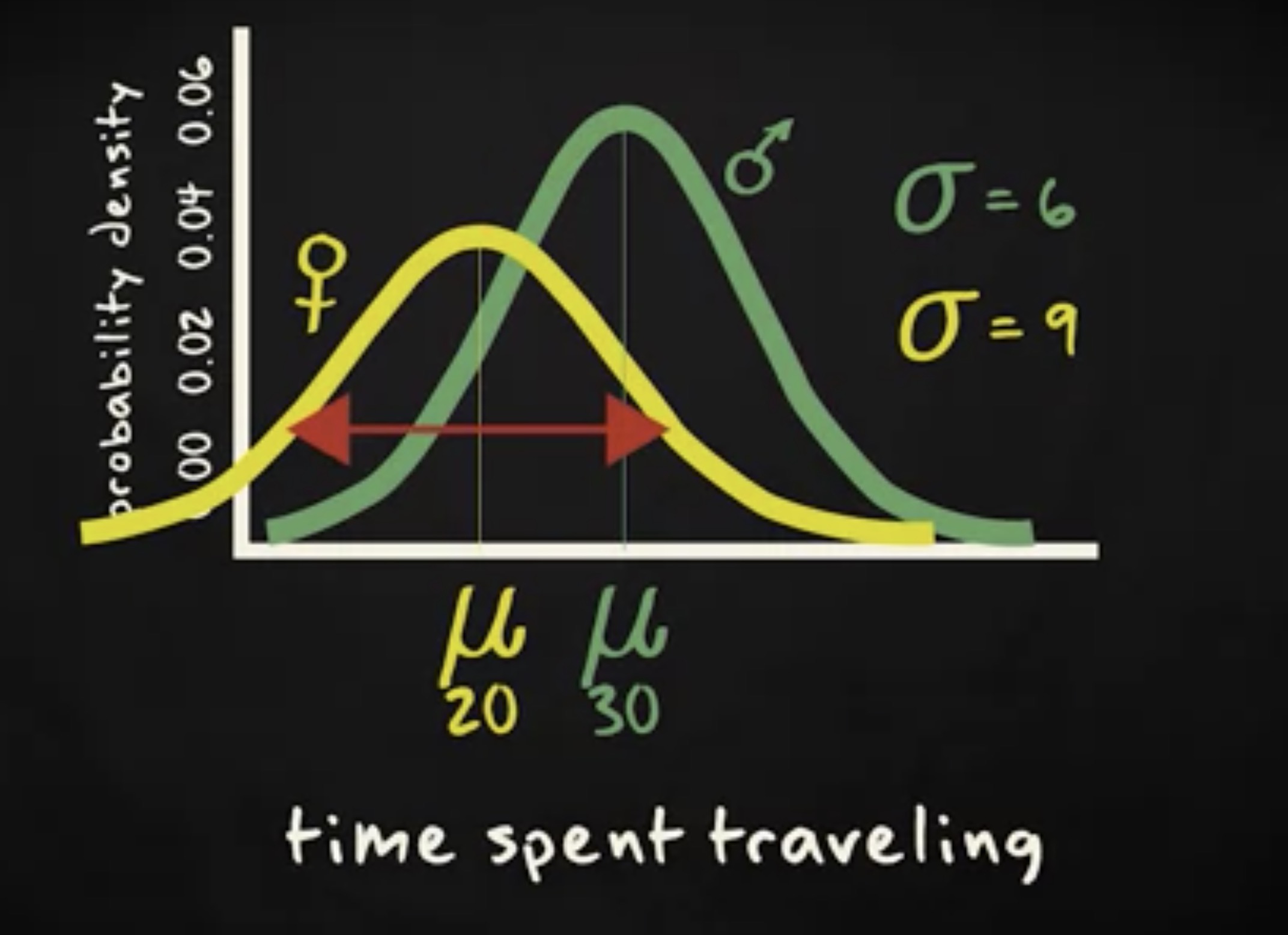
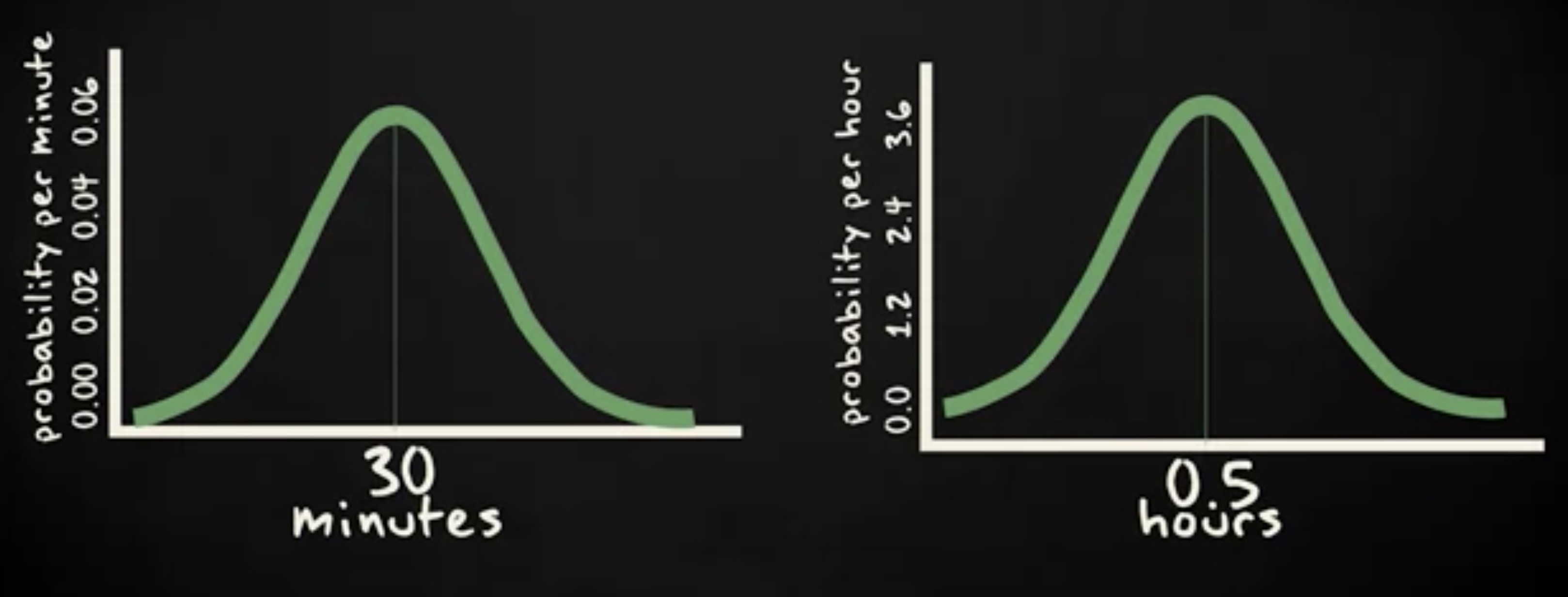
曲线还有一个属性 —— 当 x 轴的单位变化时, y 轴的单位也会发生变化。比如,你用小时而不是分钟来表示时间时,概率密度就从每分钟变成了每小时。
小结
- 正态分布或者说高斯概率密度函数,是对称的钟形曲线,其对应的累积概率函数是 S 形曲线。位置和形状完全由两个参数描述,均值和标准差。均值决定曲线的中点,而标准差决定曲线的宽度。曲线越宽,则顶点必定越低。因为曲线下的面积始终等于 1 。
- 对于一个均值为 63 ,标准差为 12 的变量 x ,速记如下:正态分布方程如下:
- 这种方程不但描述了概率分布,也描述物理世界中许多过程的结果,其中的许多扩散形式十分重要。
正态分布的概率计算
如果我们知道某个随机变量的概率分布,那我们就可以计算变量落在某个区间的概率。
这一节中吗,我将通过一个具体的例子来解释这类计算是如何进行的。
概率密度函数,经常被缩写为 pdf ,给出了随机变量每单位的概率。下面是一个出租车司机日常等待时间的 pdf 。在 y 轴你看到是每小时的概率, x 轴是以小时为单位的概率。现在,假设你是一个出租车司机,你想要知道一天中等待时间超过 7 小时的概率。你需要计算面积区域。基于图像,你可以粗造地估计面积。
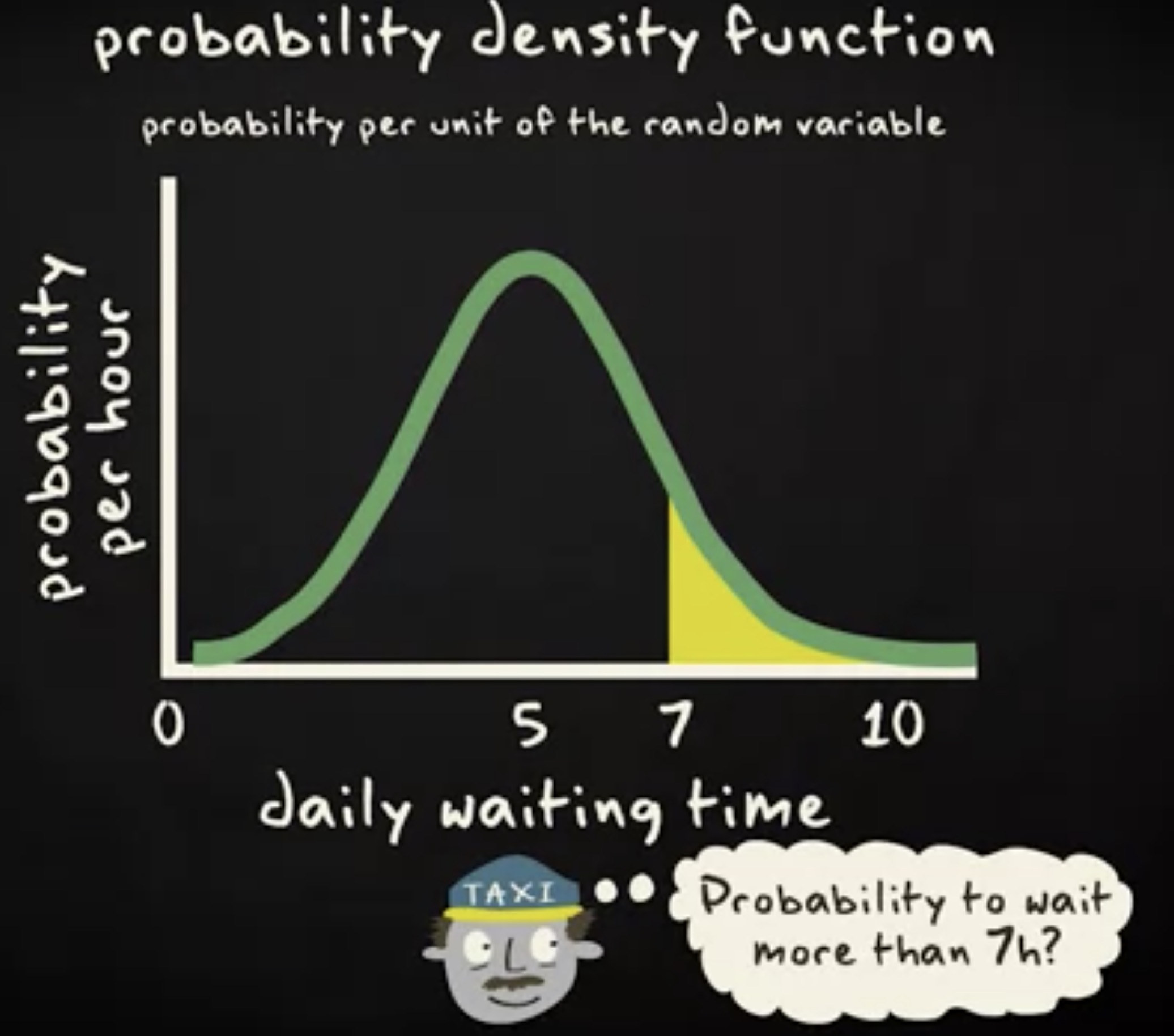
借助累积概率函数,也可以做到这一点,并且更精确。通过 x 轴 7 个小时的位置读取对应的 y 轴上的概率,再从 1 中减去这个概率。因为你关心的是长于 7 个小时而不是短于 7 个小时的概率。
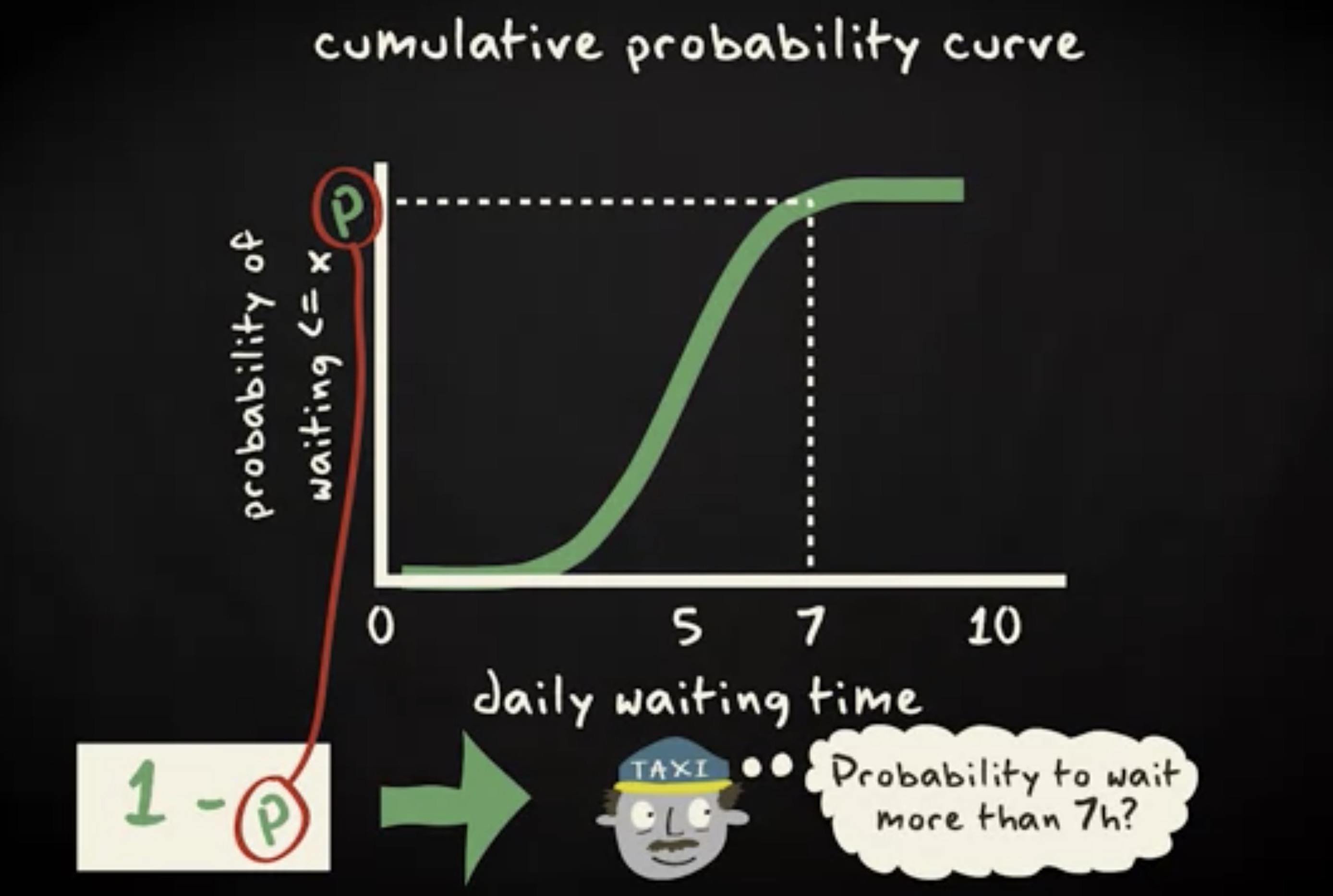
现在,让我们应用此前了解到的正态分布的等式。它是一个中点位于 μ ,宽度由 σ 定义的 pdf 形状。对应的累积概率函数在下方。
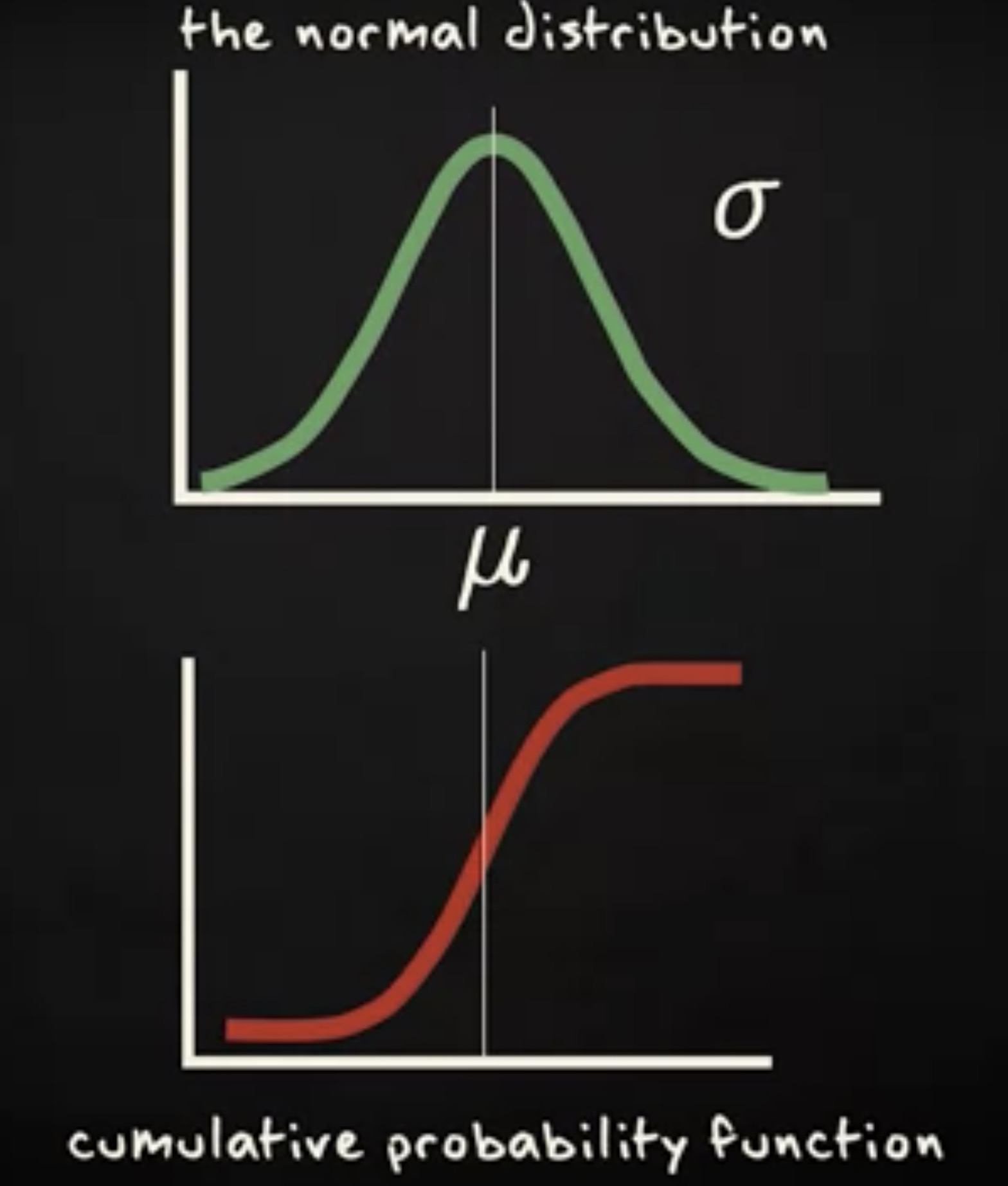
有趣的是,尽管曲线会随着 μ 和 σ 变化,距离中点一个 σ 的区间,对应的概率始终不变。
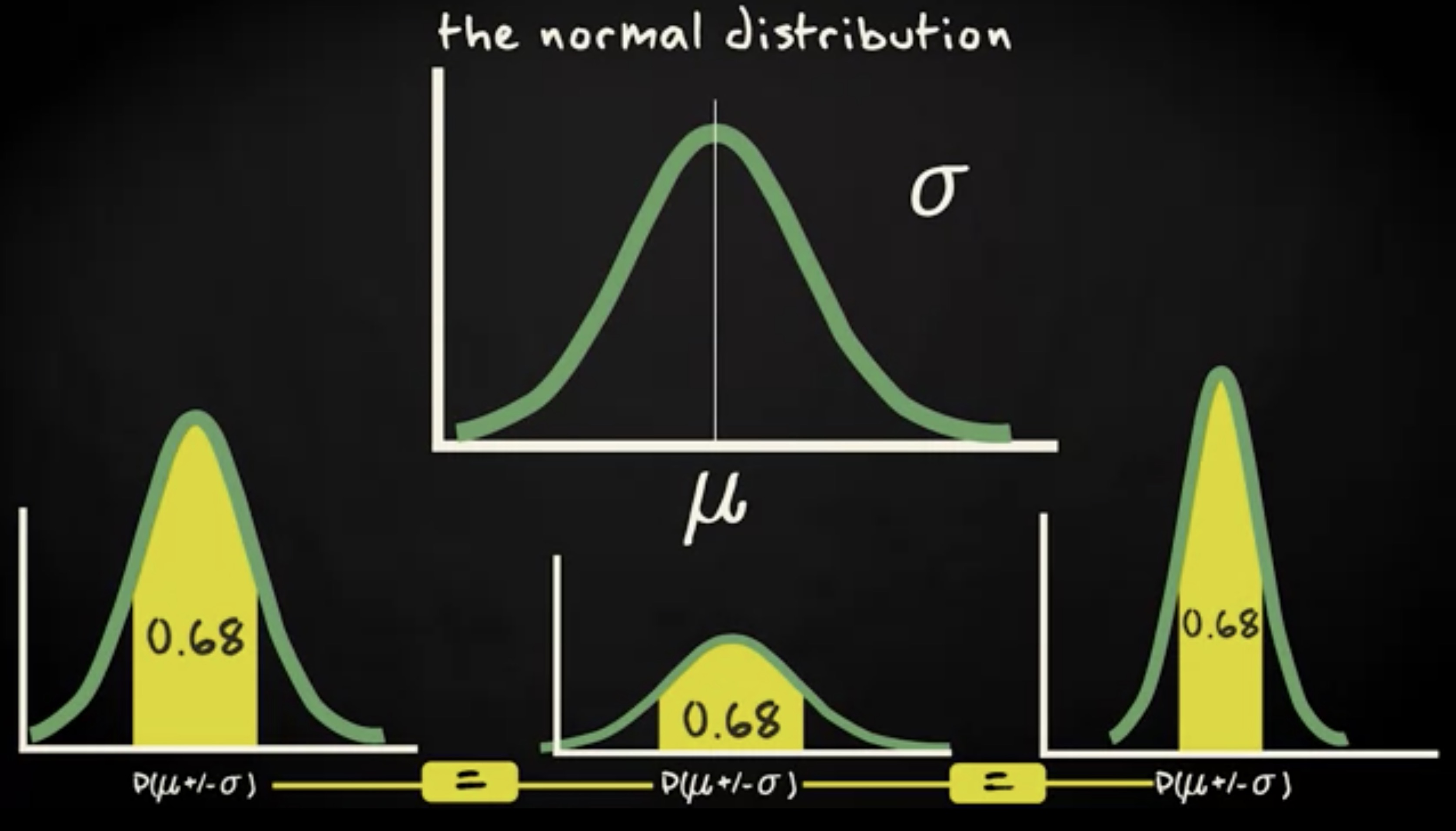
让我演示一下,假设一条曲线的均值是 20 ,标准差是 9 ,另一条曲线的均值是 30 ,标准差是 6 。对两条 pdf ,从均值减去一个标准差到均值加上一个标准差的区域,曲线之下的面积都是 0.68 。无论 μ 和 σ 分布是多少,所有的正态分布都满足这个情况。

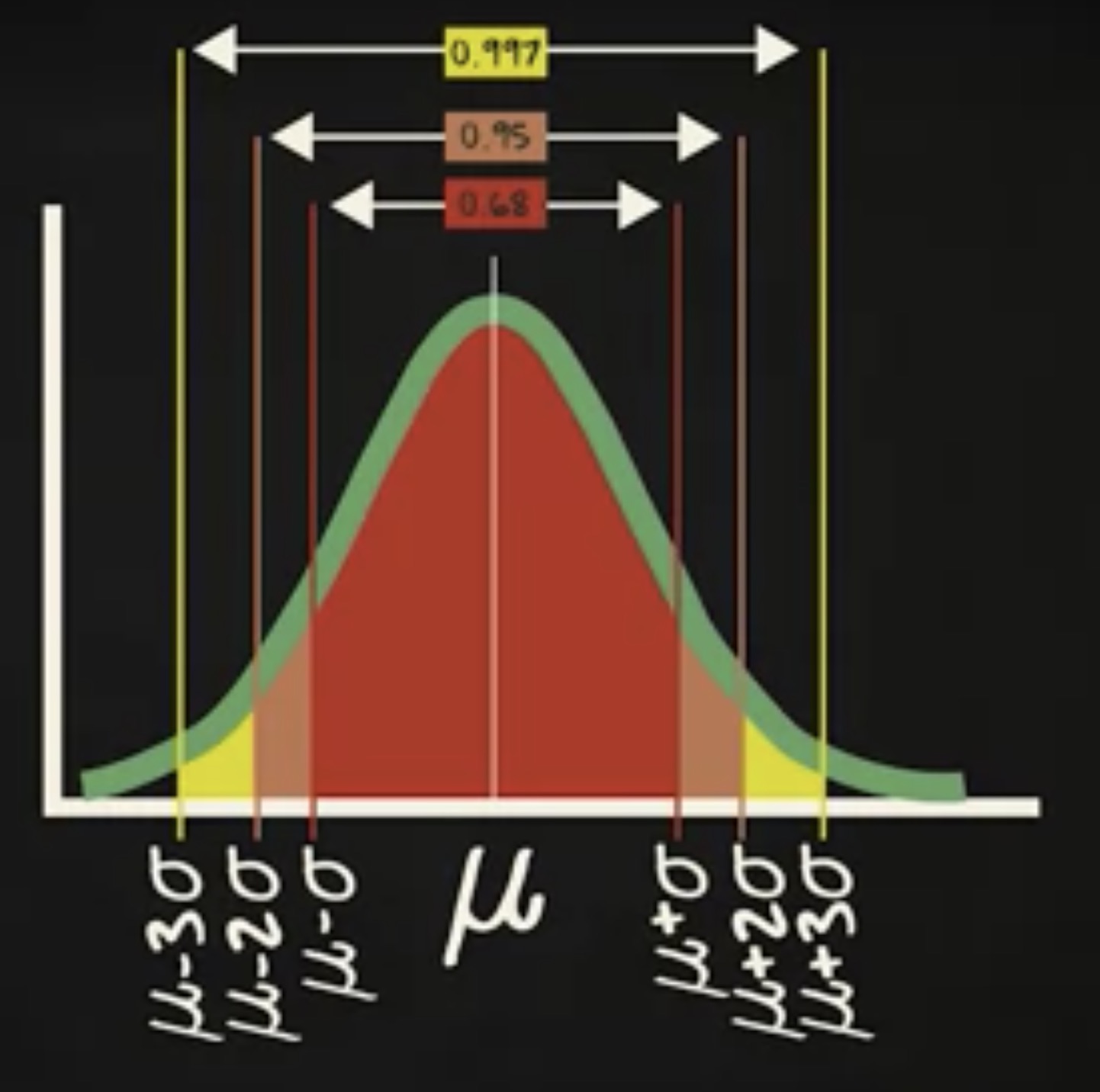
现在把区间扩展到围绕均值正负两个 σ ,区间对应的概率大致是 0.95 。

再扩展到正负三个 σ ,区间对应的概率大致是 0.997 。
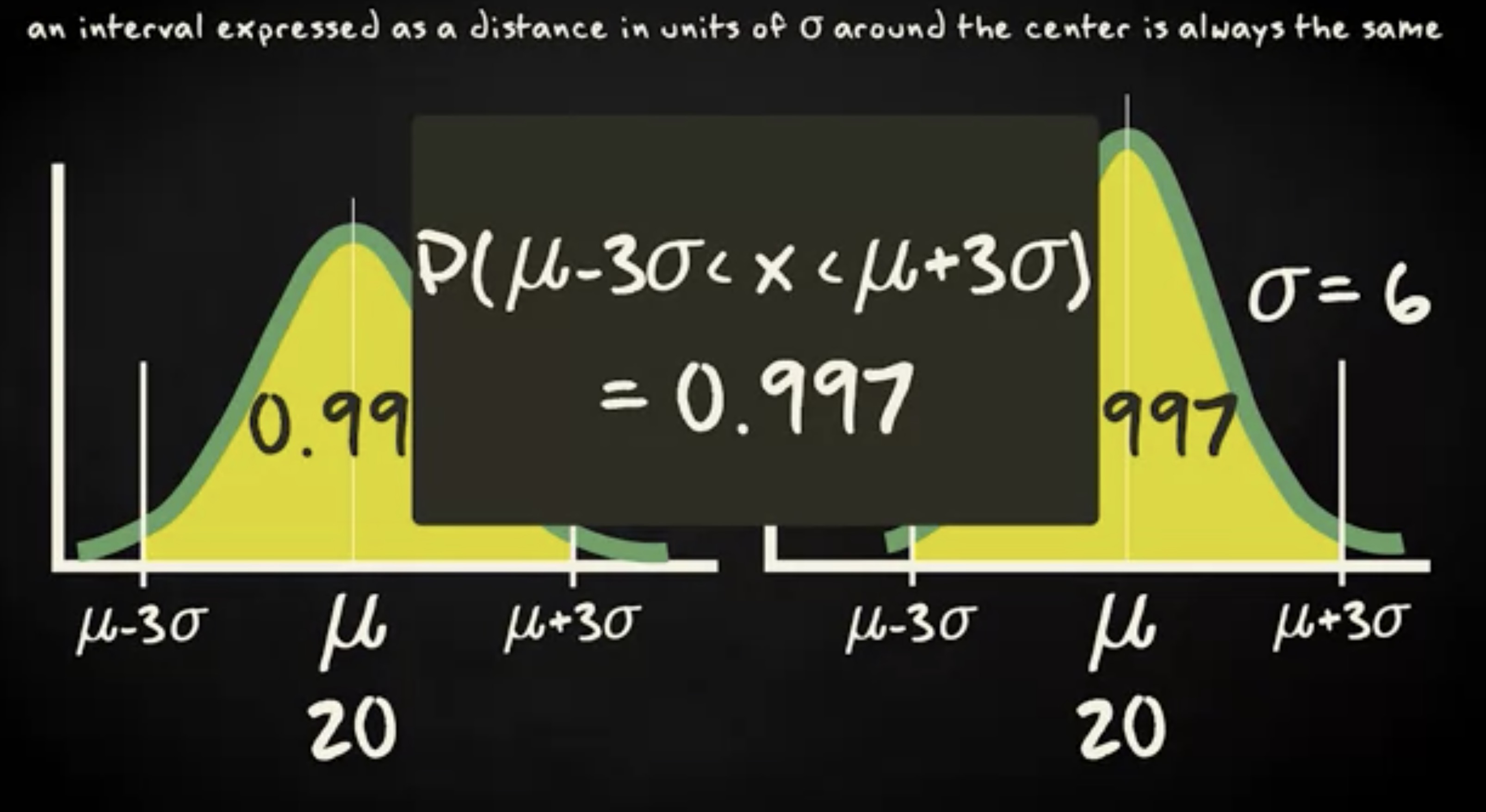
统计计算中经常用到一个、两个、三个 σ 区间的概率值。
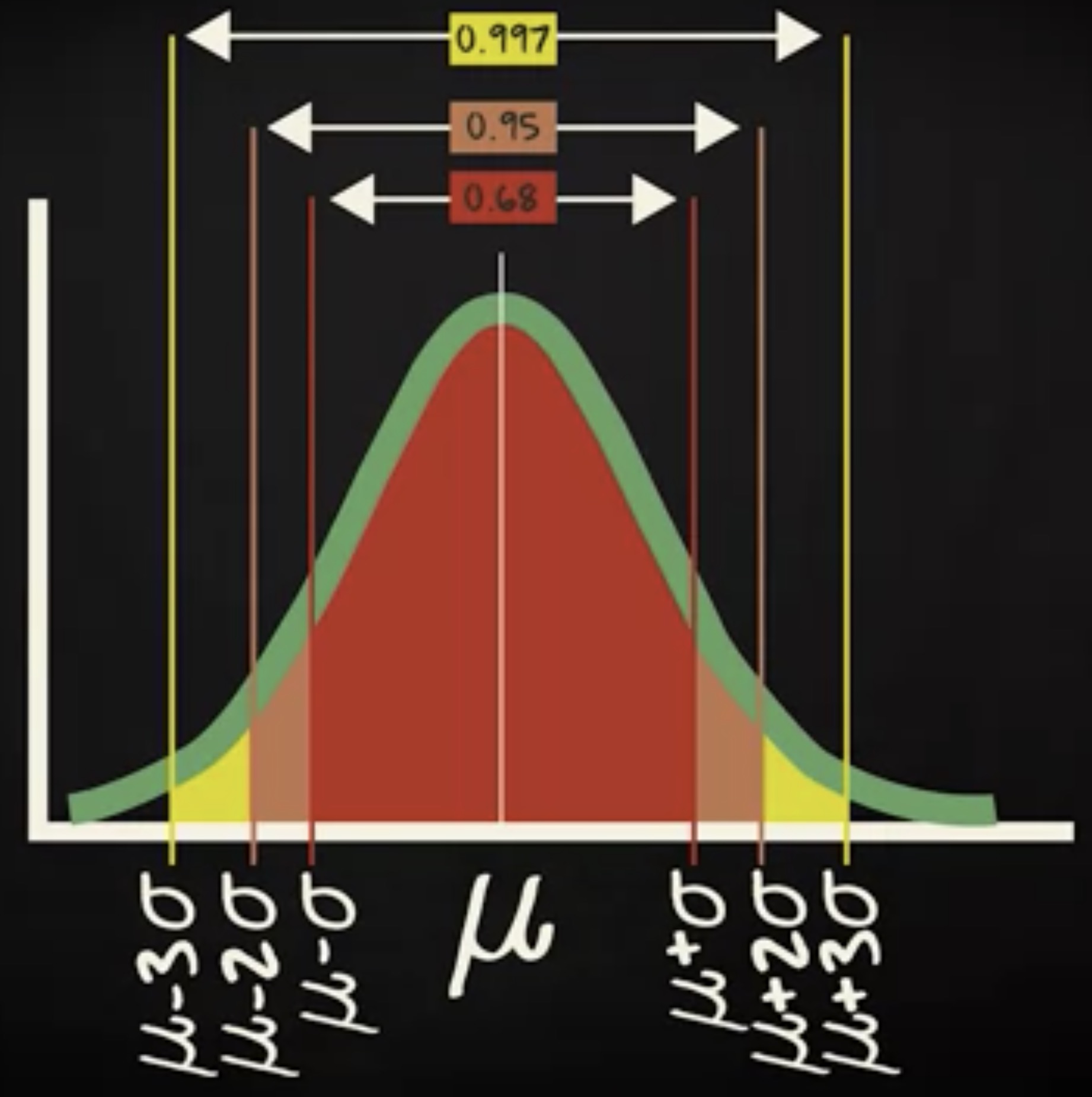
让我通过一个练习来演示一下一个、两个、三个 σ 的规则。假设你在一周中花在通勤上的时间服从正态分布,均值 40 分钟,标准差 10 分钟。 那 95% 的状态下,你的通勤时间会落在哪个范围。是的,它在均值减两个标准差到均值加两个标准差的区间。在这里,就是从 40 分钟减去 20 分钟到 40 分钟加上 20 分钟的区间。
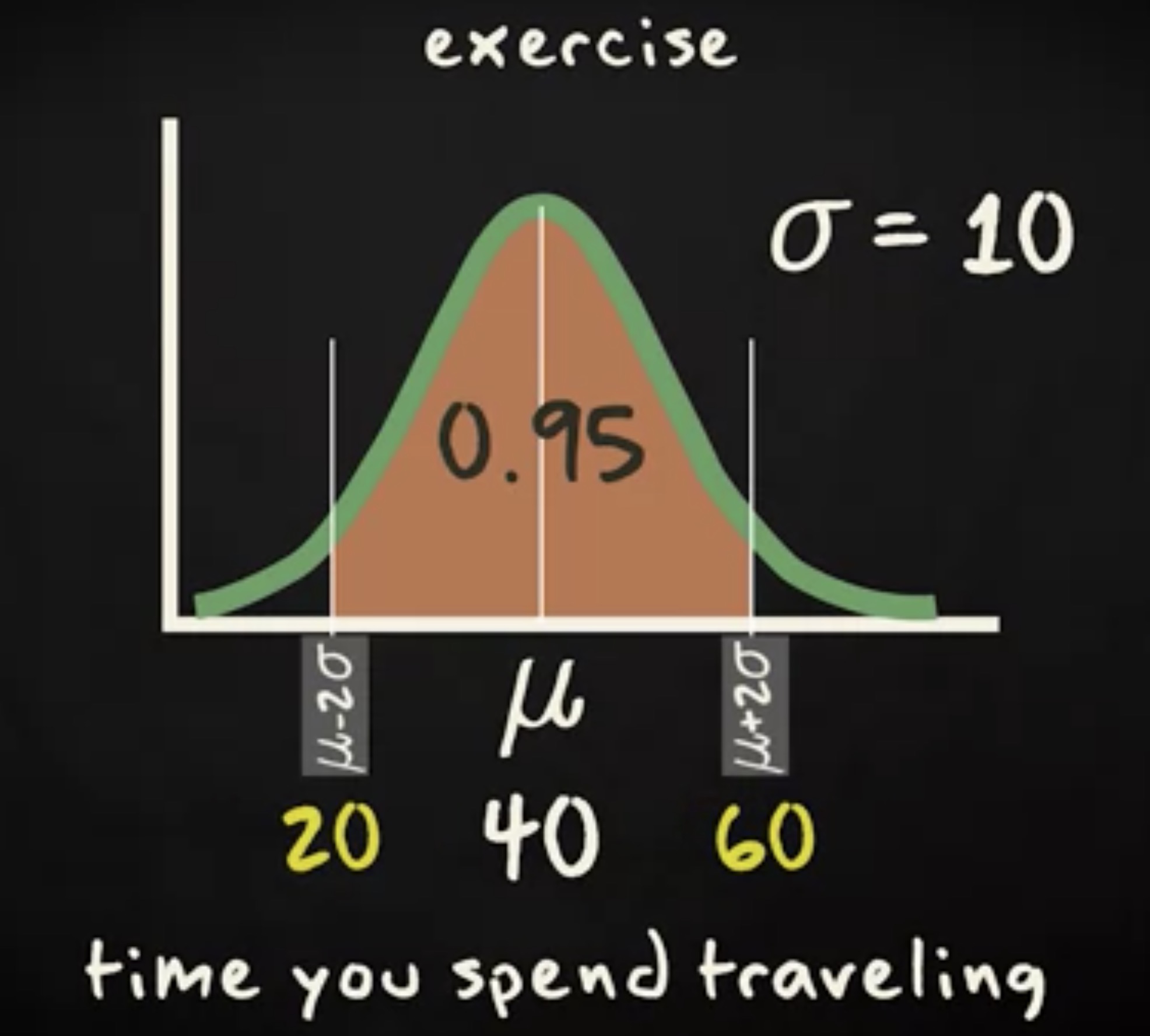
让我假定你想要知道通勤超过 50 分钟的概率,在已知平均时间是 40 分钟,标准差是 10 分钟以及一个 σ 规则的前提下,你会如何计算呢?为了解答这个问题,你需要一点创造力 —— 你知道正态分布是对称的。因此有一半的概率落在均值的一侧,继而可以知道从均值减去一个标准差到均值这个区间,概率是 0.68 的一半,即 0.34 ,于是,小于 50 分钟的概率就是 0.5 加上 0.34 ,即 0.84 。然后取补集,即 1 - 0.84 ,等于 0.16 。
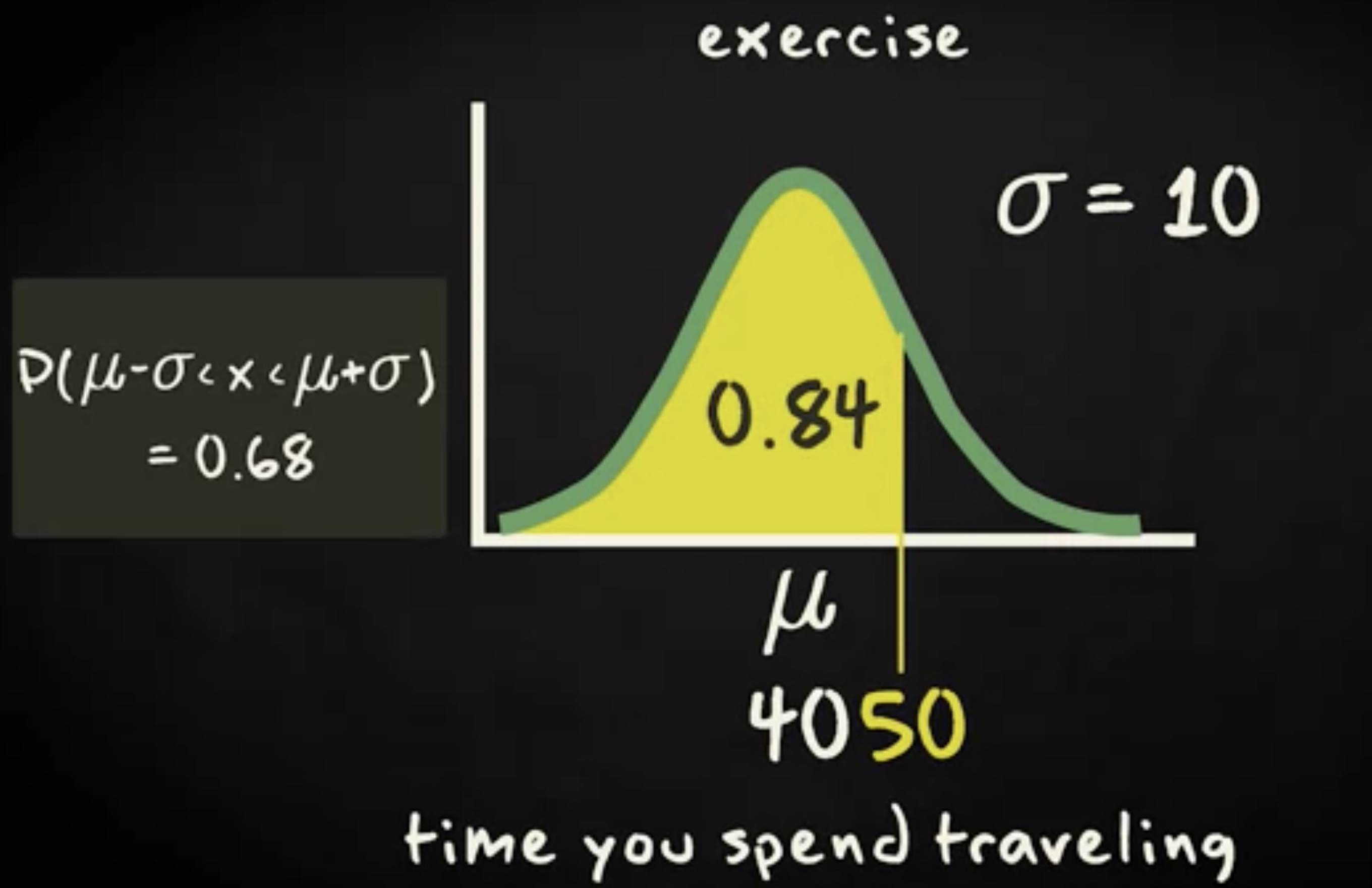
小结
- 基于概率密度函数,你可以计算随机变量落在给定区间的概率,通过估算曲线在那个范围下的面积。借助累积概率函数,通过读取 y 轴对应的概率值也能做到这一点,并且更精确。
- 对于一个服从正态分布的变量来说,围绕均值的区间,有一个固定的概率对应关系。
标准正态分布
在计算器和计算机还不得的时代,正态分布有一种非常重要的特殊形态 —— 标准正态分布 (standard normal distribution) ,也被称为 z 分布 (z-distribution) 。不过即便在今天,标准正态分布仍被高频使用,用于快速计算和呈现分析结果。
这一节中,我将解释标准正态分布的属性和应用。
尽管距离均值 1 个, 2 个, 3 个标准差的概率值很有分析的价值,仍有许多不在这些位置上的情况需要计算概率。
举个例子,比如距离均值 1.3 个标准差的概率。实际上,为了表示距离均值任意数量个标准差的意思,我们选择字母 z 。 这些 z 值的概率分布是一个均值为 0 ,标准差为 1 的正态分布,也被叫做为标准正态分布,或者 z 分布。
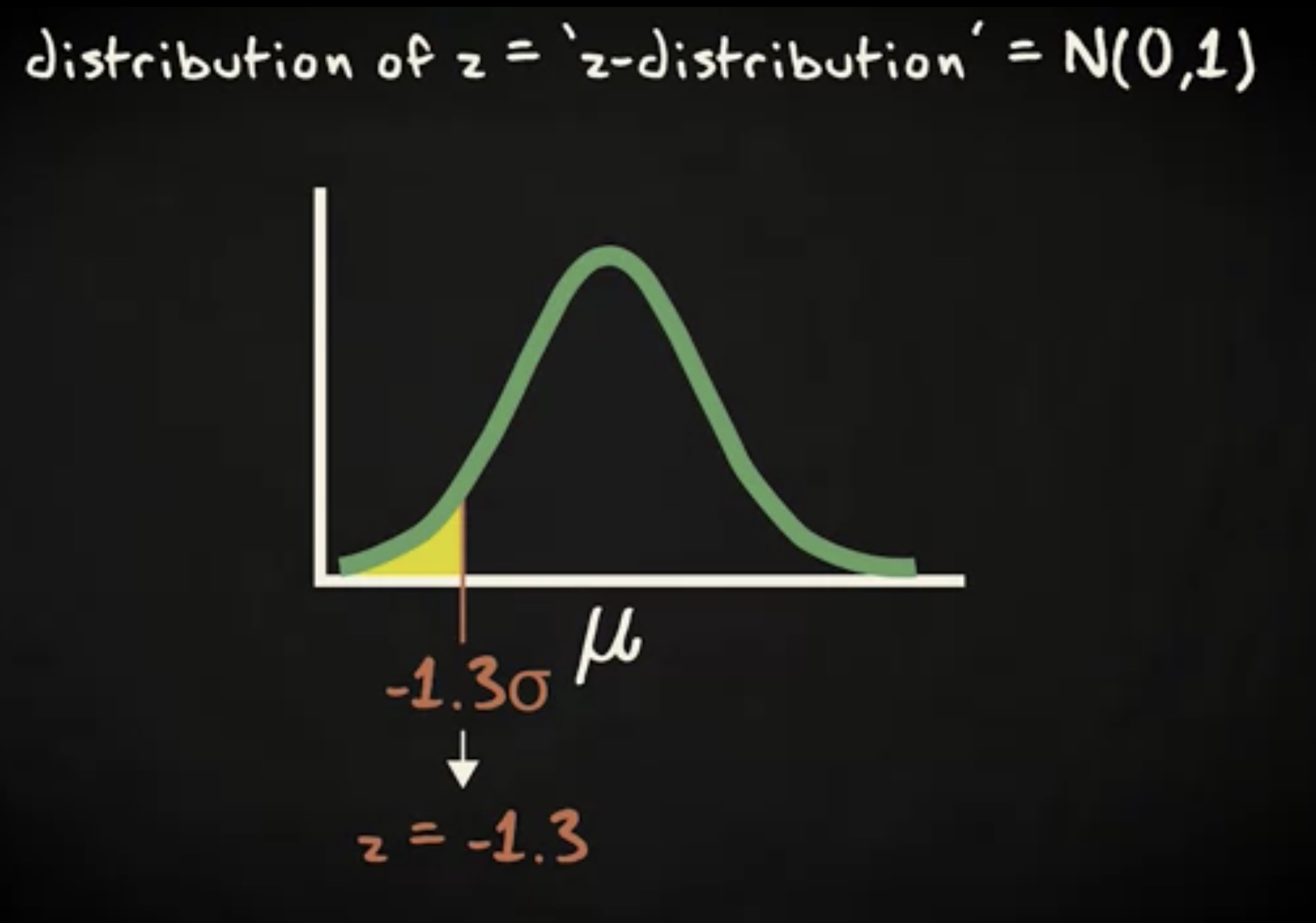
z 分布的累积分布常常用表格来呈现。下面这份表格给出一个正态分布的随机变量的累积概率,位置通过均值加上 z 个标准差偏移来确定。
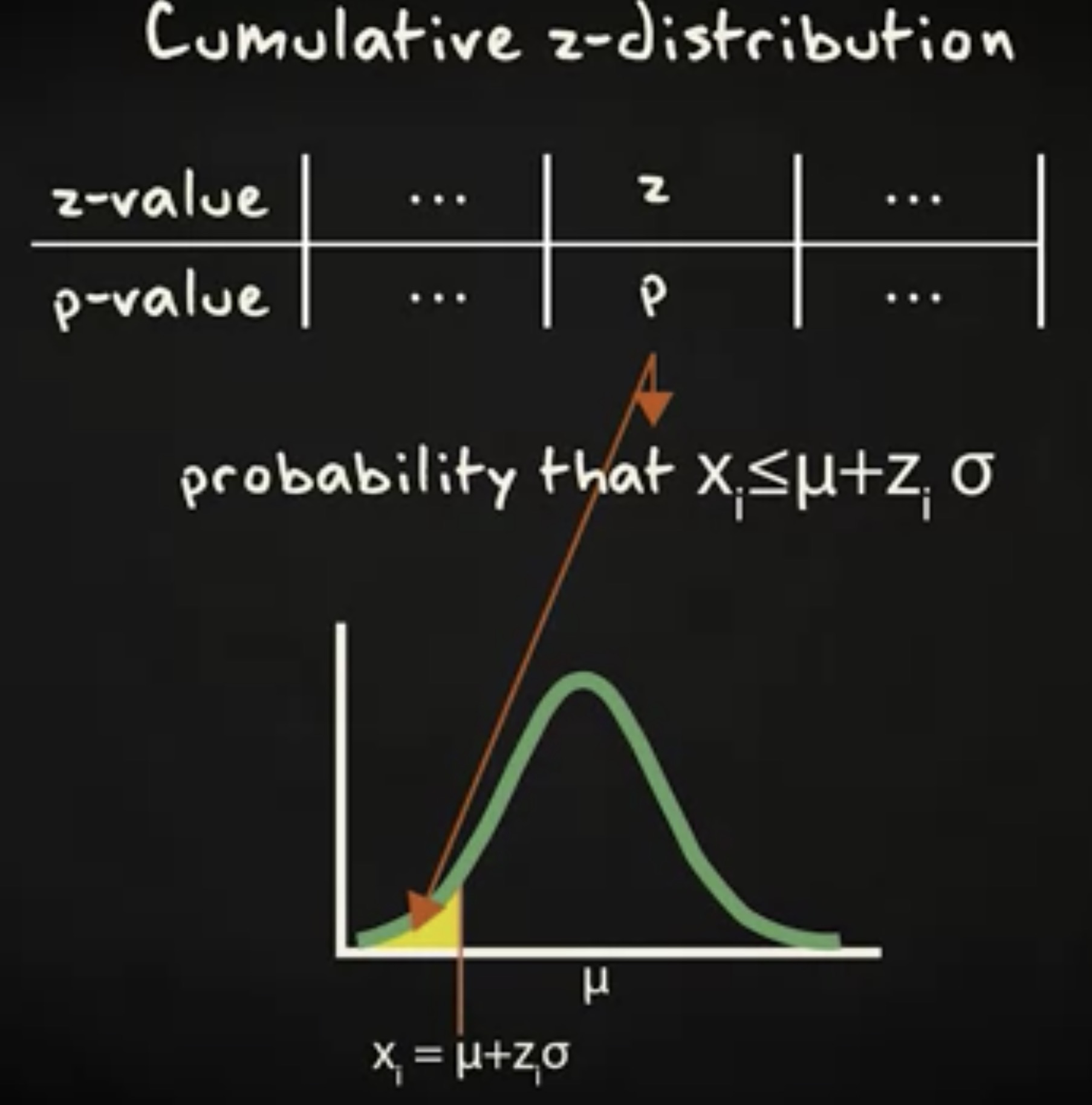
这份表格同时展示了 z 值和关联的累积概率。

如你所见,从值 -2.00 开始,以很小的步长增长,要累积到接近 1 的地方,列表会很长。因此,我们通常采用另外一种更简洁的形式来呈现 —— 用 z 值第 1 位小数作为一条边,第 2 位小数作为另一条边。
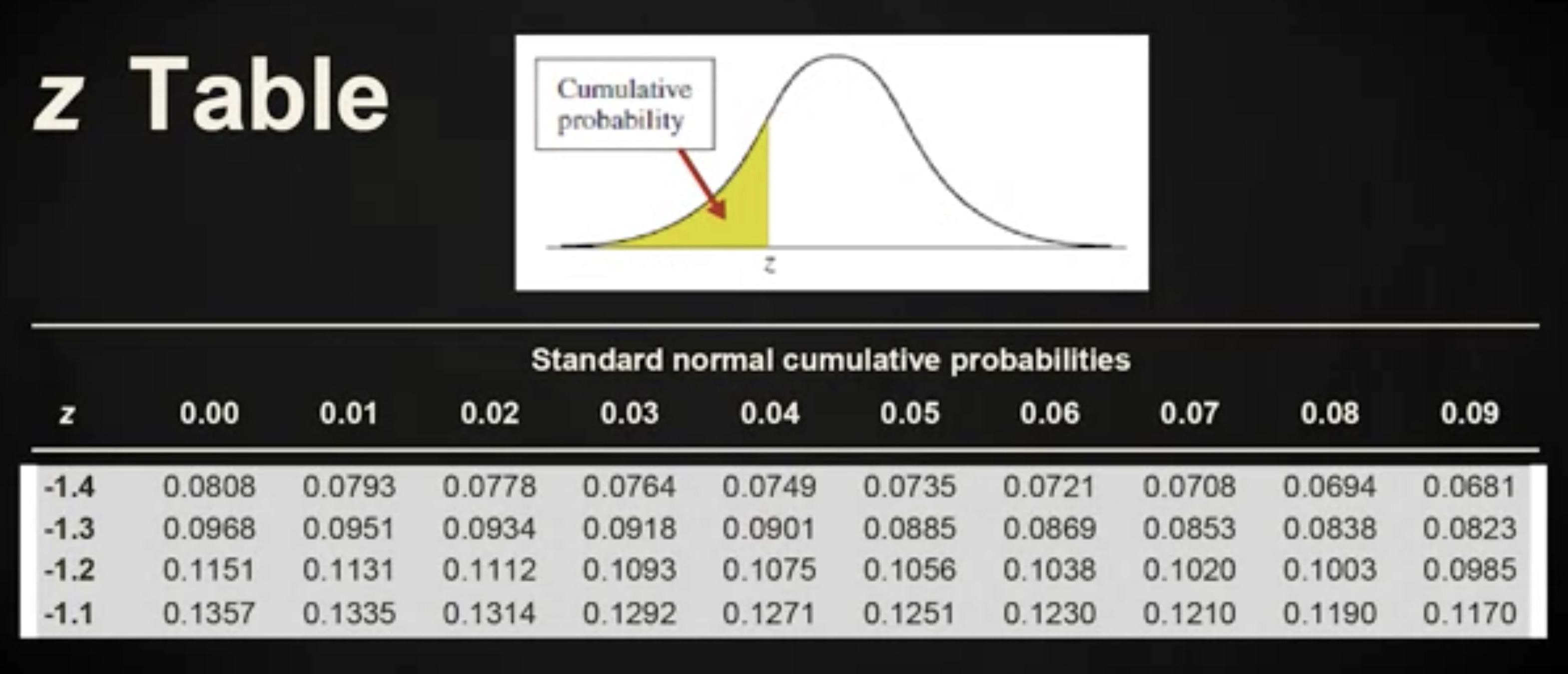
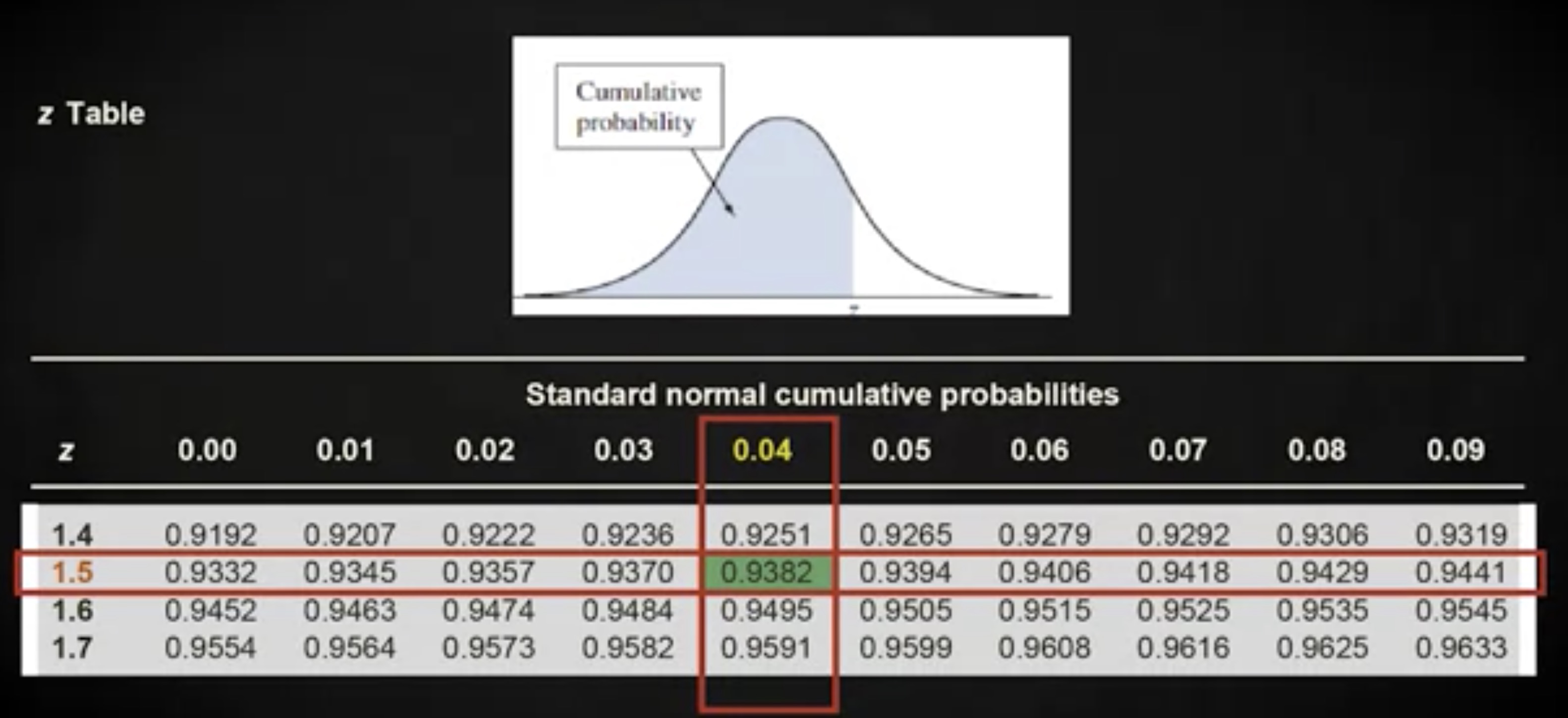
基于这样一个表格,你能够基于给定的 z 值,快速地找到与之关联的累积概率。比如,为了找到 z 值等于 1.41 的累积概率,你先选择 1.4 , 然后选择 0.01 ,最后找到对应的概率是 0.92 。

但如果我们是从一个普通的正态分布开始,该如何拿到 z 呢?首先,你需要这样考虑:对于一个随机变量 X 的某个值 x ,要把它看成均值加上 z 个标准差偏移。这个时候,你想知道 z ,可以反过来借由 x ,均值和标准差。把等式做一个调整,你发现 z 值等于随机变量的观察值与均值之差,再除以标准差。
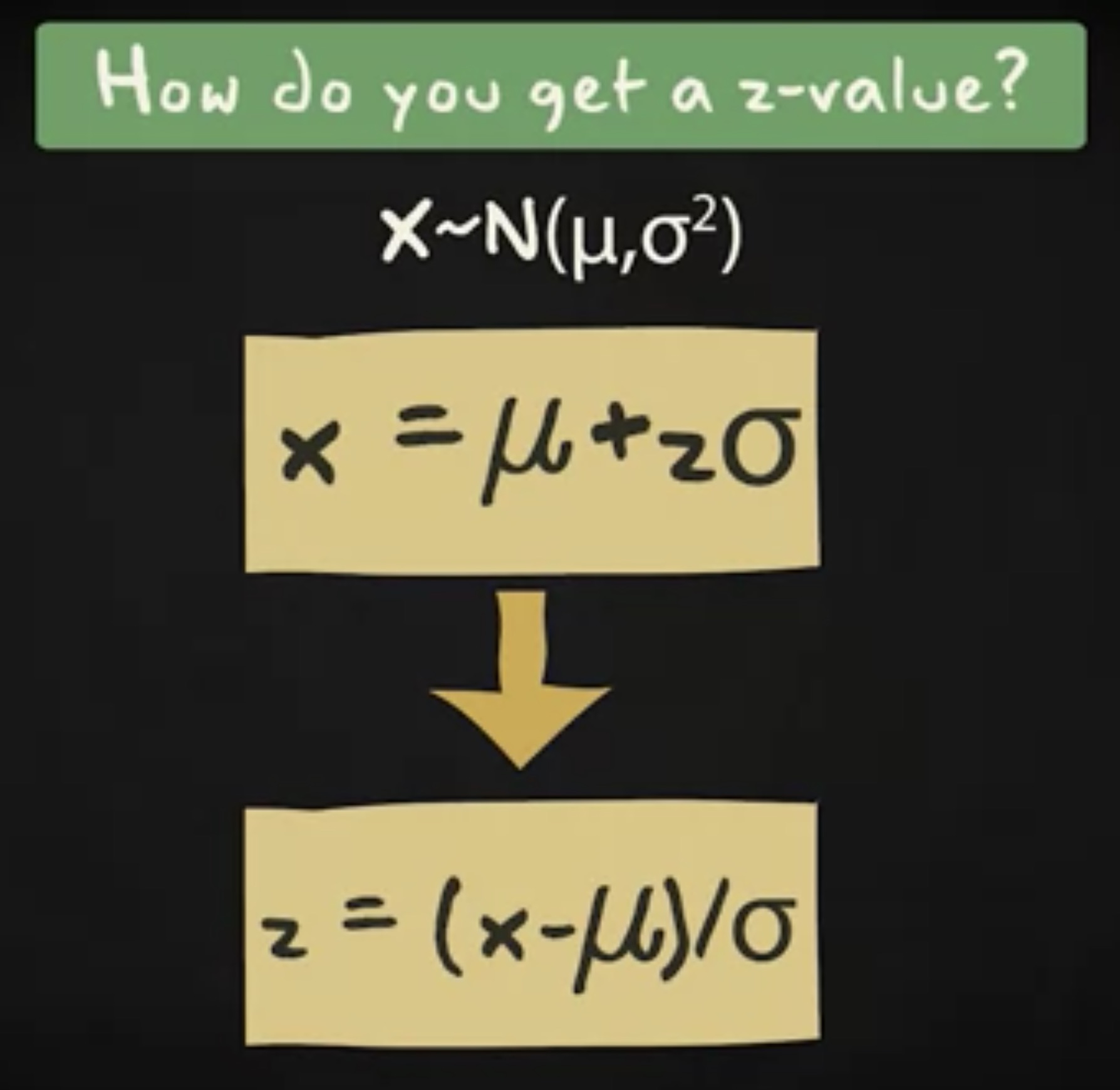
让我们把上面的变换应用到实例中。想象一群绿脚大雁每年秋天都要从波罗的海地区迁徙到欧洲的大西洋海岸。迁徙持续时间服从均值为 4 天,标准差为 1.3 天的正态分布。现在,要计算这群大雁在 6 天内到达迁徙目的地的概率。
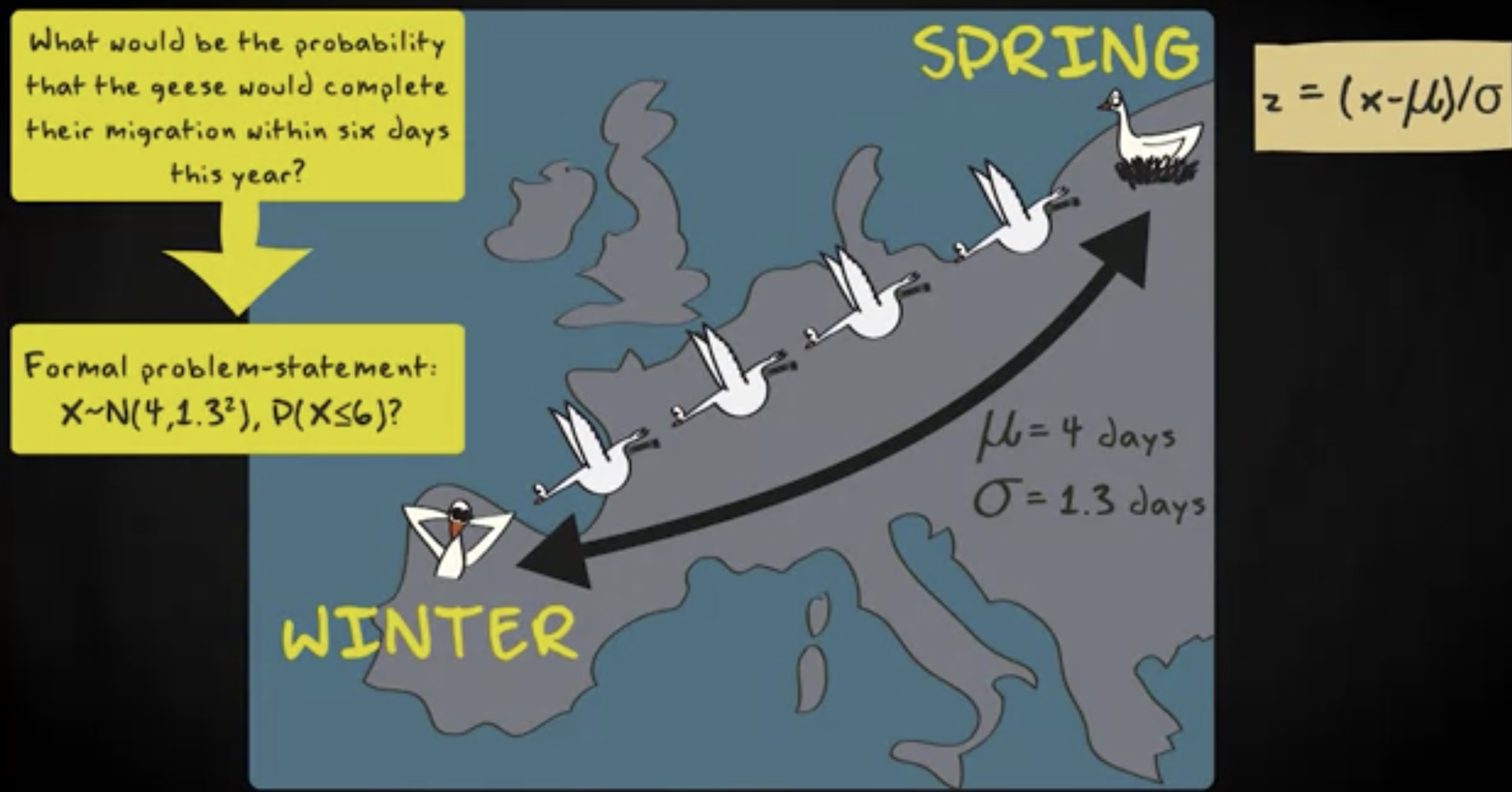
首先,你需要对 6 天做 z 变换 (z transform) ,通过 x 减去均值,然后除以标准差,得到 1.54 。下一步,在表格中查询 z 值,找到匹配的概率概率。
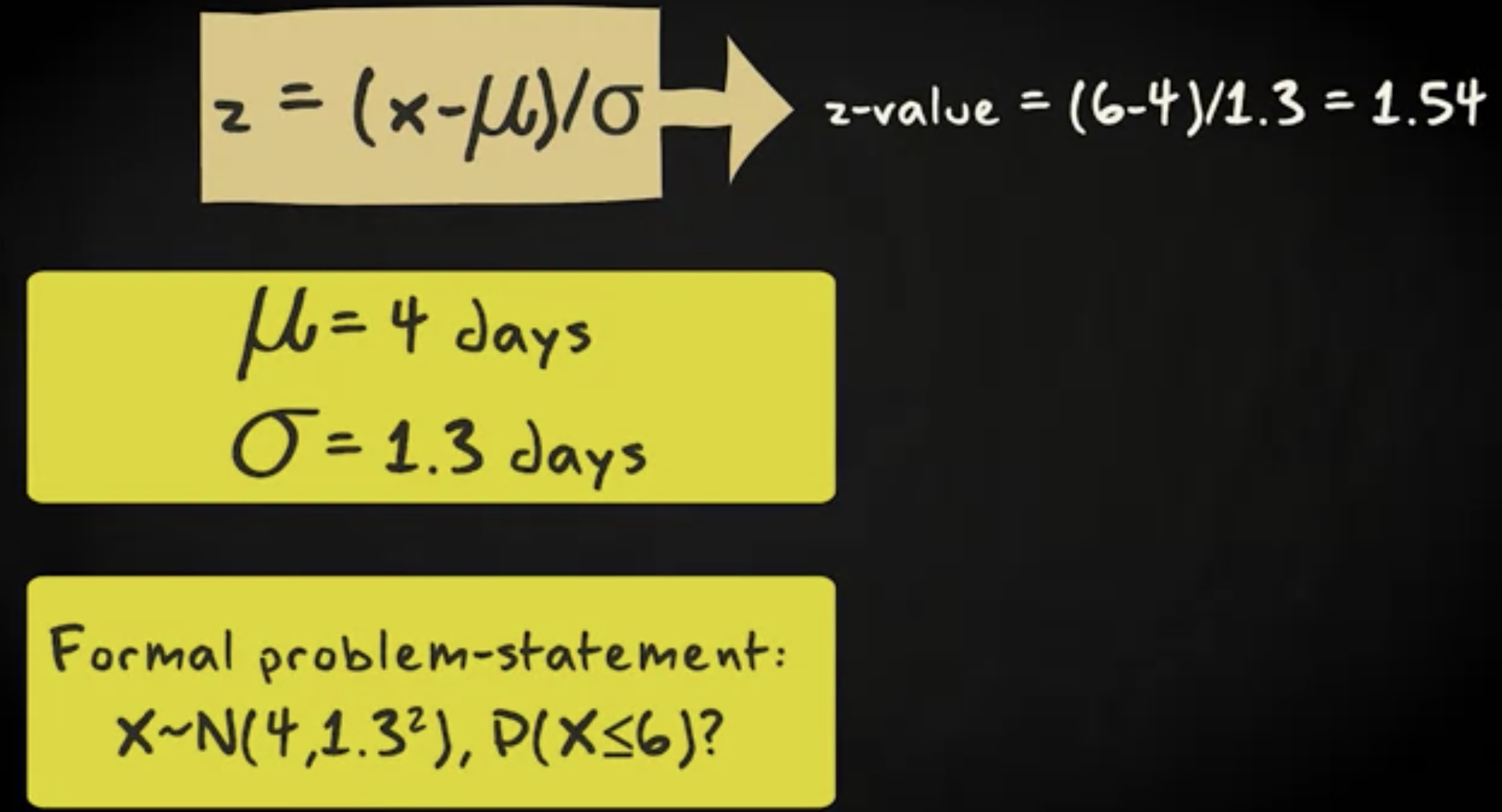
如你所见,这个 z 值匹配的是概率 0.9382 ,这就是针对前面问题的答案 —— 这群大雁在 6 天内完成迁徙的概率。
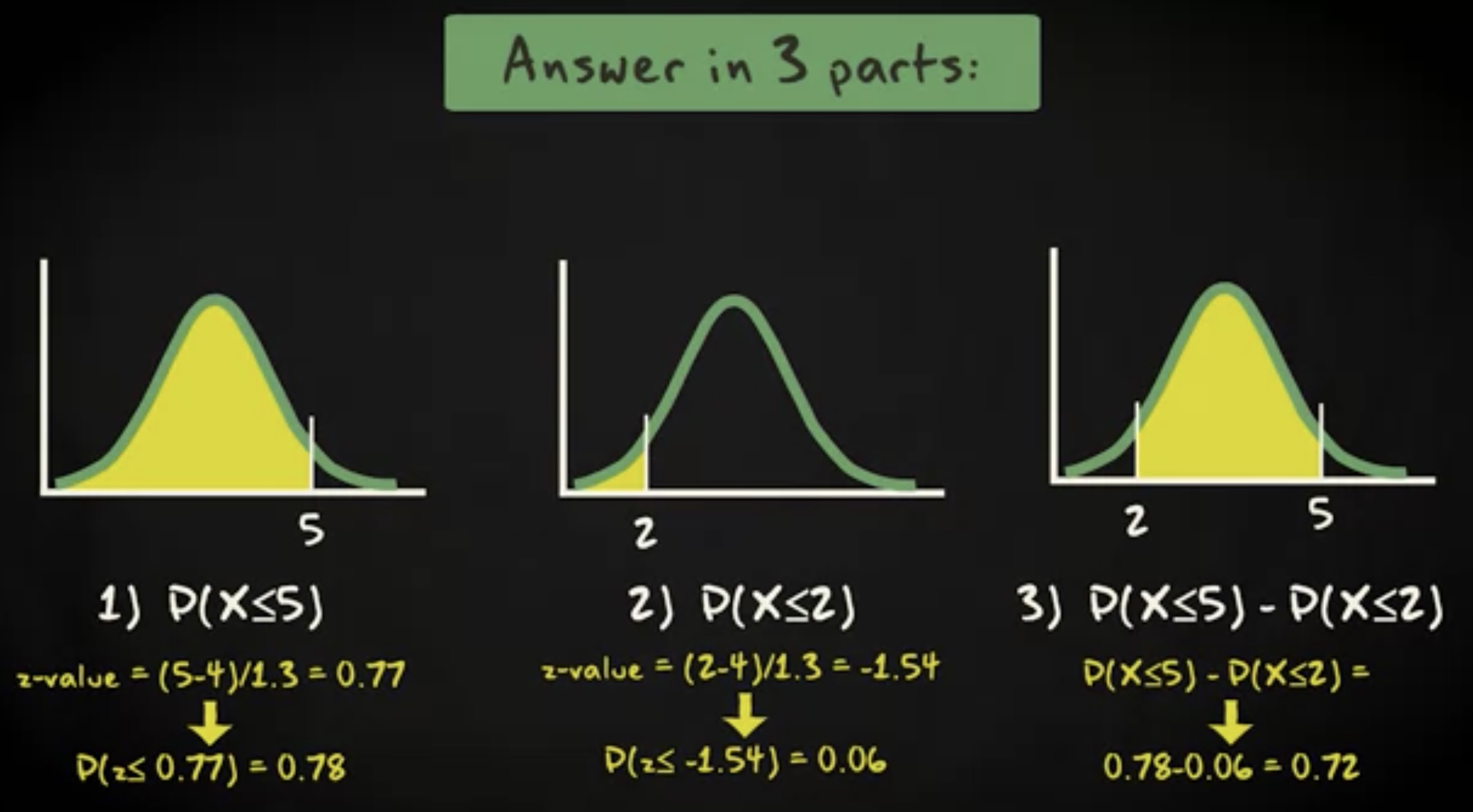
如果是迁徙时间介于两天到五天之间,你又会怎么计算呢?下面是问题的正式描述:

首先,计算小于 5 天的概率,然后计算小于 2 天的概率。然后将两个概率相减,就得到要求的范围: 2 天到 5 天。小于 5 的概率是 0.78 ,小于 2 的概率是 0.06 。从 2 到 5 的概率等于两者之差,即 0.72 。
现在,让我们休息一下。我们已经看到,可以把任意正态分布转换成标准正态分布或者说 z 分布的变量,通过减去均值再除以标准差来实现。然后,借助表格化的分布数据,我们能找到小于某个值、大于某个值或者介于两个值之间的概率。因此,如果你已经有一个概率了,你想反过来找出对应的随机变量的值,这时候要怎么做呢?
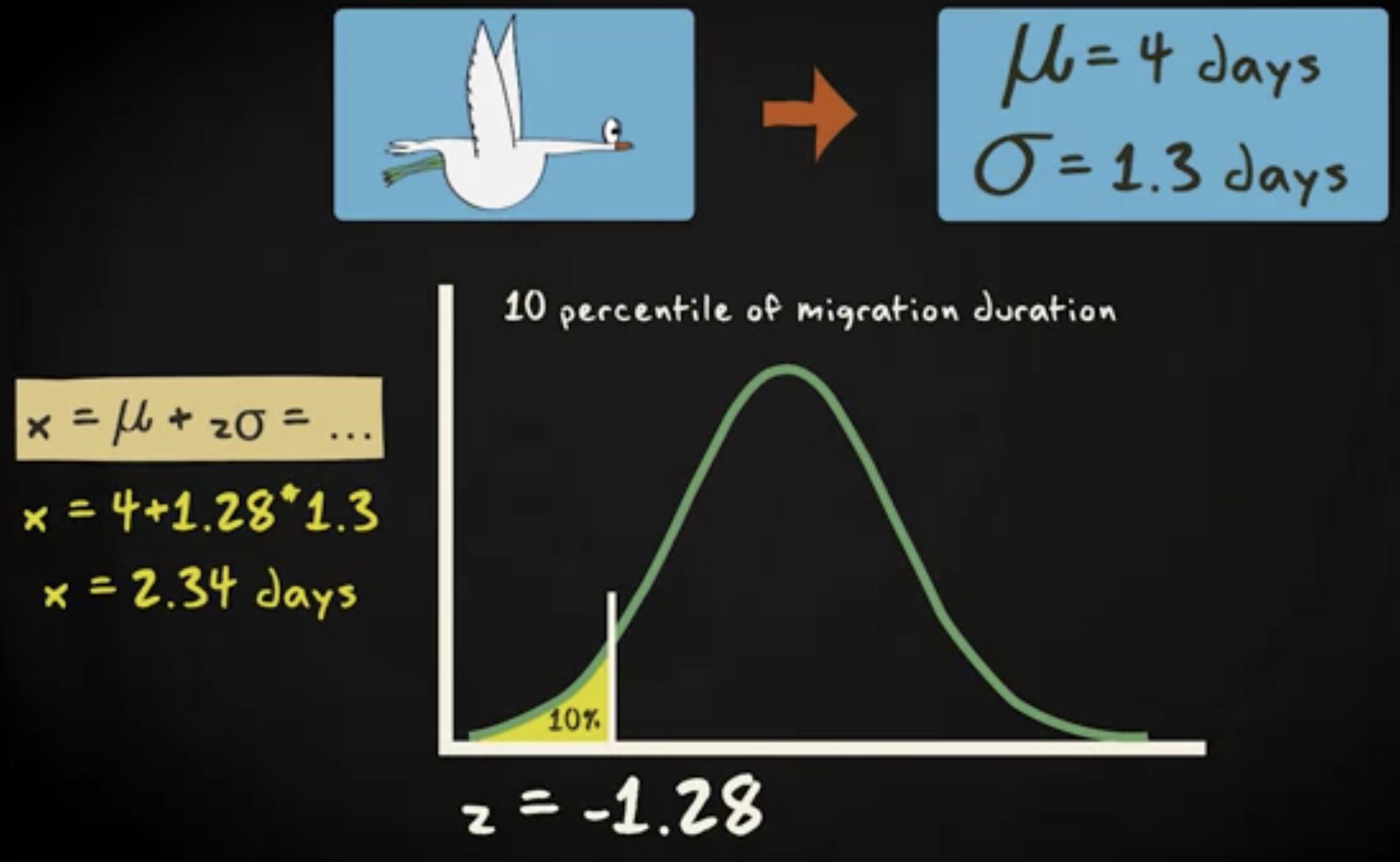
别担心,做法几乎相同,只需要反过来。还是用前面大雁迁徙的粒子。假设它们平均需要 4 天,标准差 1.3 天来完成迁徙。那么,你可以找出迁徙持续时间的十分位。
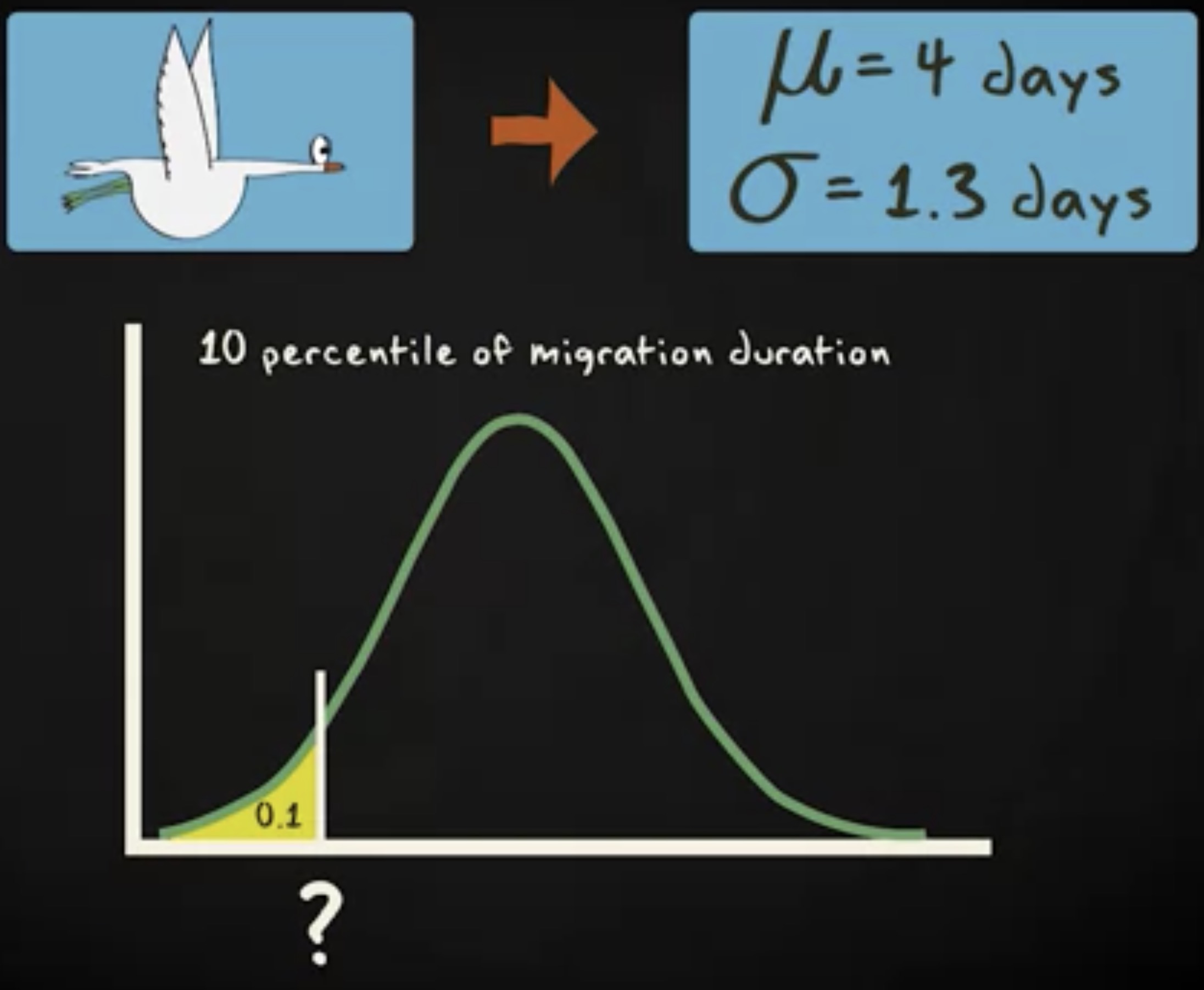
持续时间的十分位意思是迁徙时间少于所有情况中的 10% 的情况,或者多于所有情况中的 90% 的情况。首先,你通过查表看到最接近概率 0.1 的 x 的值,它是 - 1.28 ,然后借助公式 $ x = μ + zσ $ ,你得到 x 的值时 2.34 天。
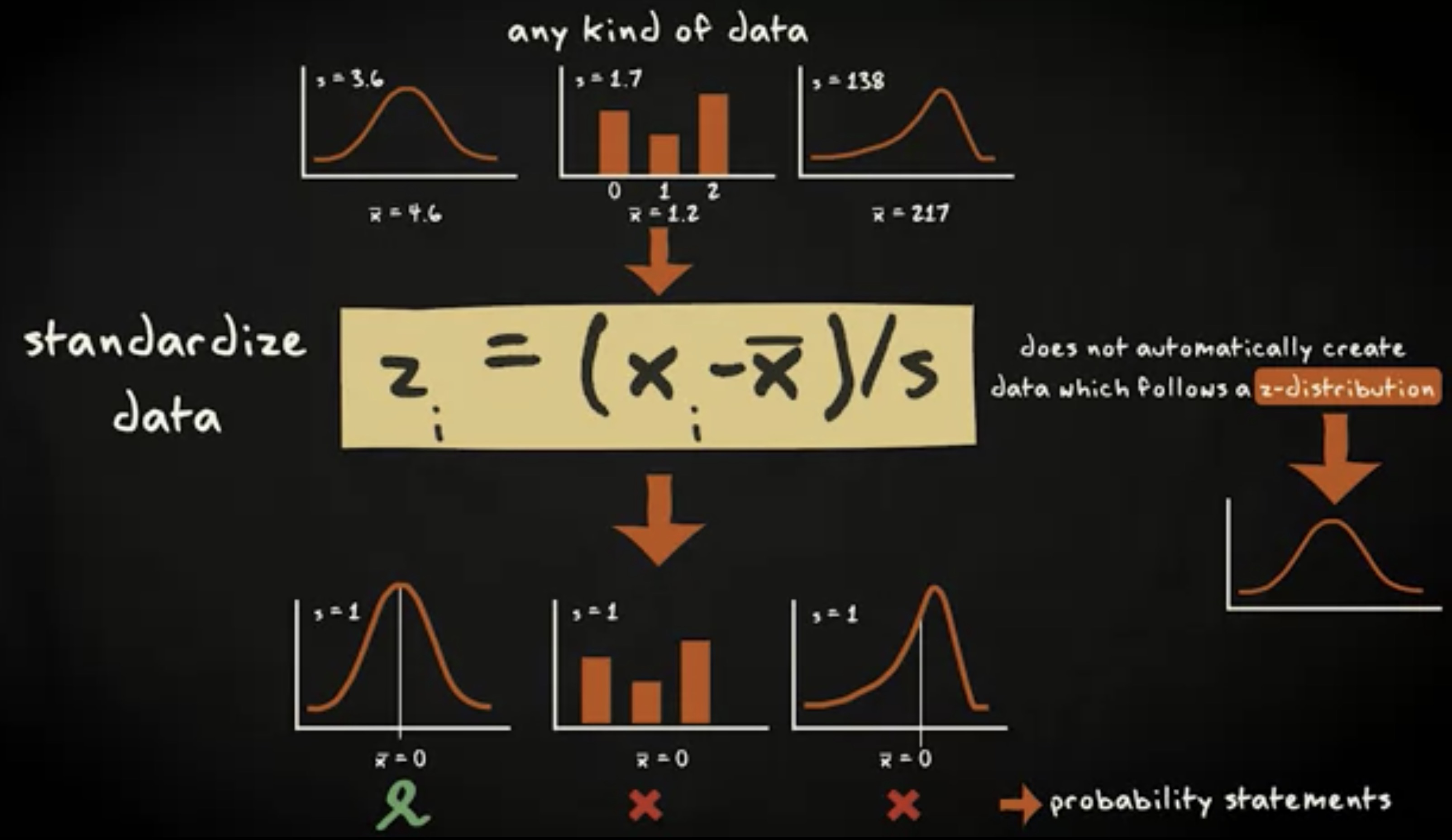
最后,我想强调的是, z 变换适用于任意类型的数值数据,它会得到一个均值为 0 ,标准差为 1 的数据集,并且不包含对数据潜在分布的假定。因此,标准化数据是一个好方法,尤其是你想在不同的案例间做比较的时候。不过, z 变换并不能自动地创造出服从 z 分布并且能允许你计算概率的数据。你要得到 z 分布的数据,前提是数据本来就服从正态分布,并且你能算出均值和标准差。
小结
- z 变换可以应用于标准化数据,取得一个均值为 0 ,标准差为 1 的数据集,无论原始数据集是何种分布。当已知数据富服从正态分布时,可以基于 z 分数,借助对应 z 分数的累积概率表格来做概率计算。
- 对于给定的 x ,你通过从中减去均值,再除以标准差的方式来获得 z 。 z 表格提供了匹配 z 值的累积概率。这些概率指的是随机变量小于或者等于 x 的概率。相反地,对于给定的概率,你可以在表格中找出 z 值,然后计算出匹配这个值的 x 。

