欢迎关注微信公众号「Swift 花园」

非科学的方法 (Non-scientific Methods)

为了知道为什么我们需要科学方法，让我们来看看在日常生活中人们的认知基于什么。

人们可能会基于 直觉 (intuition) 或 信念 (belief) 而认为某事是正确的。

让我们来看下我对我的猫 Misha 所拥有的坚定信念：我相信 Misha 在所有人中最爱我 —— 我就是知道他爱我胜过其他所有人，我能在内心深处感受到。那么这种信念算不算是知识的坚实基础？并不是，简单地相信某件事并不会让它成真。我们坚信不疑的事情可能最后被证明是假的。还有，如果有人持相反的观点会怎样？如果我的未婚夫认为 Misha 爱他多一些呢？

仅仅通过较量我们的观点，是无法得出谁对谁错的。

我们可以数每个观点的支持人数，然后得到一个大部分或是 一致同意的观点 (consensus) ，但是这也不能作为知识的坚实基础。仅因为大部分人认同某事是并不意味着它就是真的。几世纪以来，几乎人人都认为地球是平的，但结果证明他们错了 —— 地球是圆的。

另一个知识的来源就是 权威 (authority) 的观点。这也不是一个很好的来源。一些诸如政治领袖、专家、科学家等权威的观点，也只是一种观点。权威或许能接触到更多或更好的知识，但他们出于个人利益也会推动自己的观点被大众接受，他们的职业和名誉都依赖于此。假设我的未婚夫找到了一个懂猫语的人，那人声称 Misha 更爱我的未婚夫。当然我会对这一专业观点表示怀疑，尤其当他是受我未婚夫雇佣的时候。我可以找到我自己的猫咪专家来和未婚夫的猫语者打擂台。但这时我们又有两个相反的观点了 —— 我们需要的是 证据 (evidence) 。

那么我们该如何用证据来解决 Misha 更爱谁的争论呢？

假设我总是 观察 (observe) 到每次下班回家后 Misha 总会过来坐在我的腿上而不是我未婚夫的腿上。我就运用了对客观世界，也就是对下班后 Misha 坐谁的腿上的 观察 (ovservation) 来证明我说的 Misha 更爱我这个 命题 (statement) 。

以 随机观察 (casual observation) 取证得到的认识，比前面其他方法了解到的认识更有根据一些，但这仍然不够好。 因为人们并不十分擅长观察 。我们倾向于 选择性观察 ，并且记住与我们观念相符的事情。比如我可能恰好忘记了， Misha 在早饭的时候总是坐在我未婚夫的腿上。

除了选择性知觉外还存在许多 偏见 (bias) ，会让随机观察成为一个棘手的认识来源。我们运用 逻辑 (logic) 的能力也是如此。 逻辑推理 (logical reasoning) 得出的认识看上去是有坚实基础的，但 非形式逻辑推理 (informal logical reasoning) 并不总是具有一致性。人们在日常生活中进行推理时，总会不停地出现 谬误 (fallacy) 或 逻辑矛盾 (logical inconsistency) 。

如果想获得更准确的认识，确定我们对世界的解释是正确的，那就还需要点别的东西。我们不能依赖于主观的、无法证实的来源 —— 诸如信念、观点、舆论。我们也不能相信随机观察和非形式逻辑，因为它们可能被我们的信念严重扭曲。

我们需要 系统观察 ，摒弃任何偏见，辅以一致的逻辑。换言之 我们需要 科学方法 。

科学方法 (Scientific Method)

当我们试图解释世上事物运行原理时，为了确保知识有效，我们需要科学方法，而不是依靠观点、信念、随意观察和非形式逻辑。它们都太主观且容易出错。

科学方法基于 系统观察 (systematic observation) 和 逻辑一致性 (consistent logic) 。使用科学方法，增加了我们得出正确解释的机率。同时，我们也可以通过科学方法鉴定 科学主张 (scientific claim) 、 假说 (hypothesis) ，以及鉴定在我们实证研究中用来支撑假说的那些 经验证据 (empirical evidence) 的说服力。

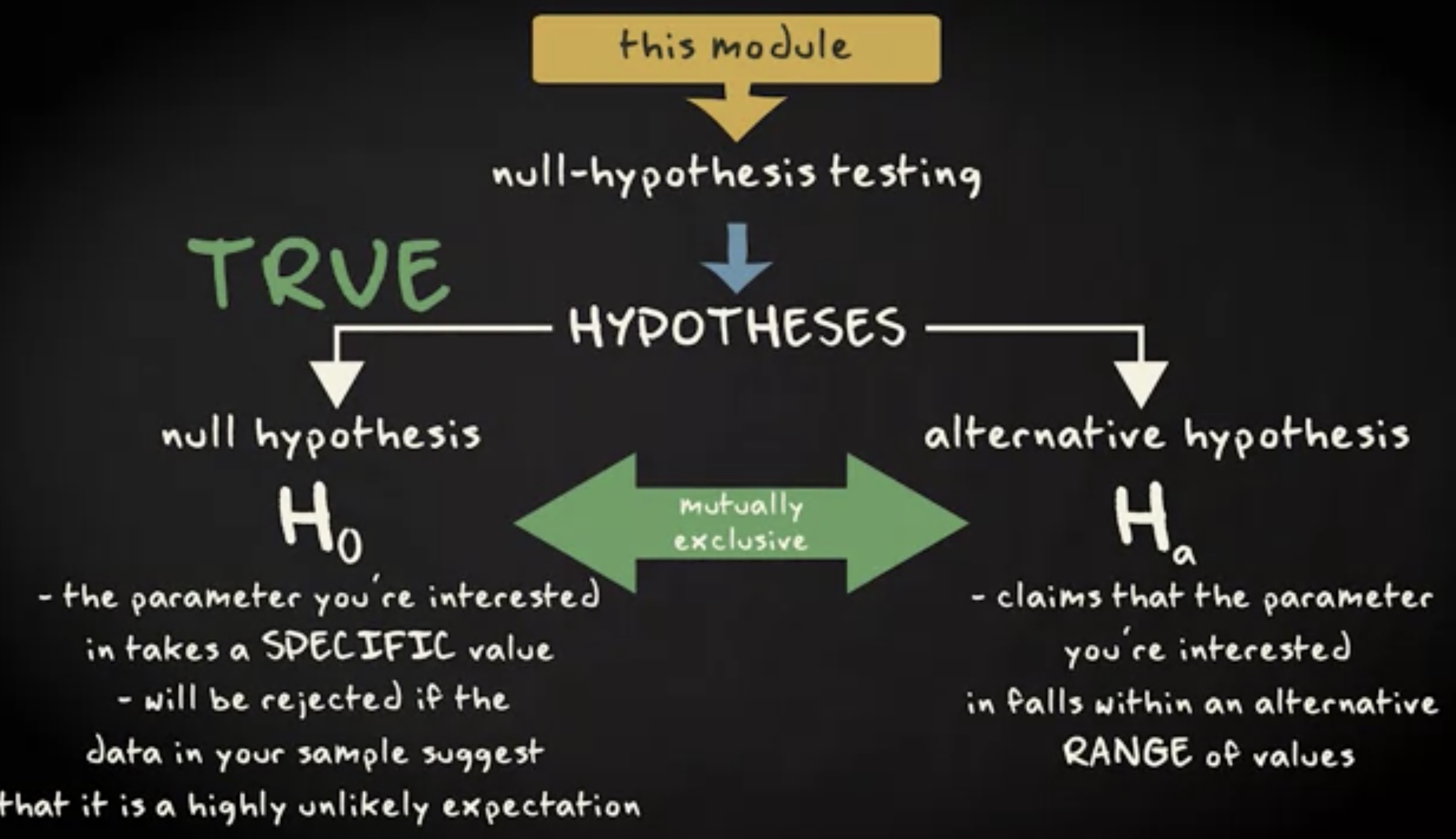
科学方法有六大原则科学方法有六大原则。如果我们的研究符合这些原则，就能归为科学研究。

这个假说亦可以与其他科学论断一较高下，为我们的世界提供尽可能最好的解释。

第一条原则是：假说应该可以 在实证中检验 (empirically testable) ，即支持或反驳假说的经验证据、物证或观测结果都是可以收集的。

比如我假设家里的猫爱我多于我未婚夫。要实证检验这个假说，我们需要收集观察结果或数据。但如何观察这只猫对我们的喜爱程度呢？我们不能询问猫的看法。假设我们都认为猫是无法像人类那样表达爱意的，那就没什么好观察的了。所以这条假说不符合实证可检验的原则。

第二原则是：可重复性 (replicability) 。一项研究及其发现结果都应该具有可重复性。这意味着重复原研究是可以得到一致结果的。

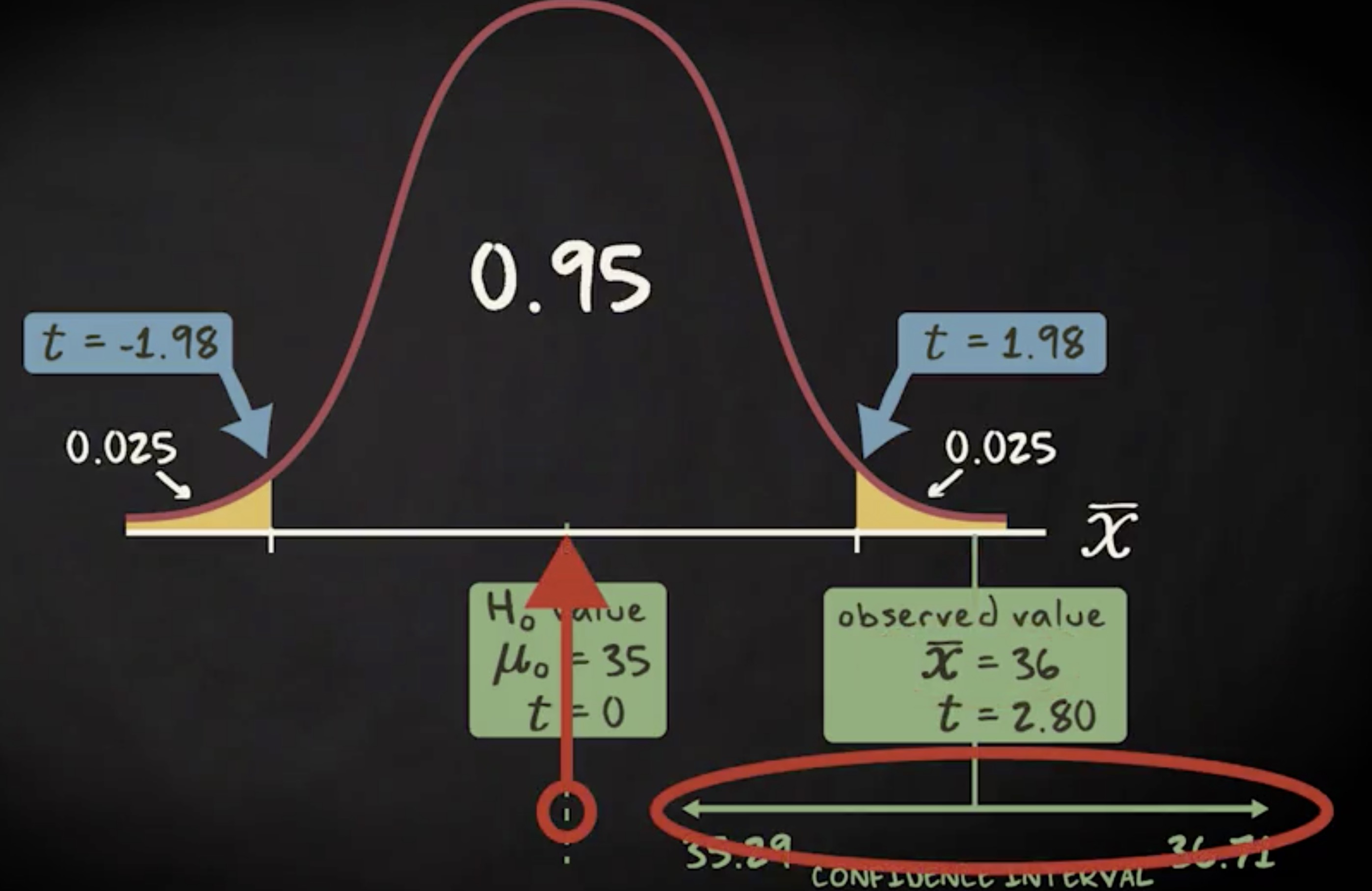
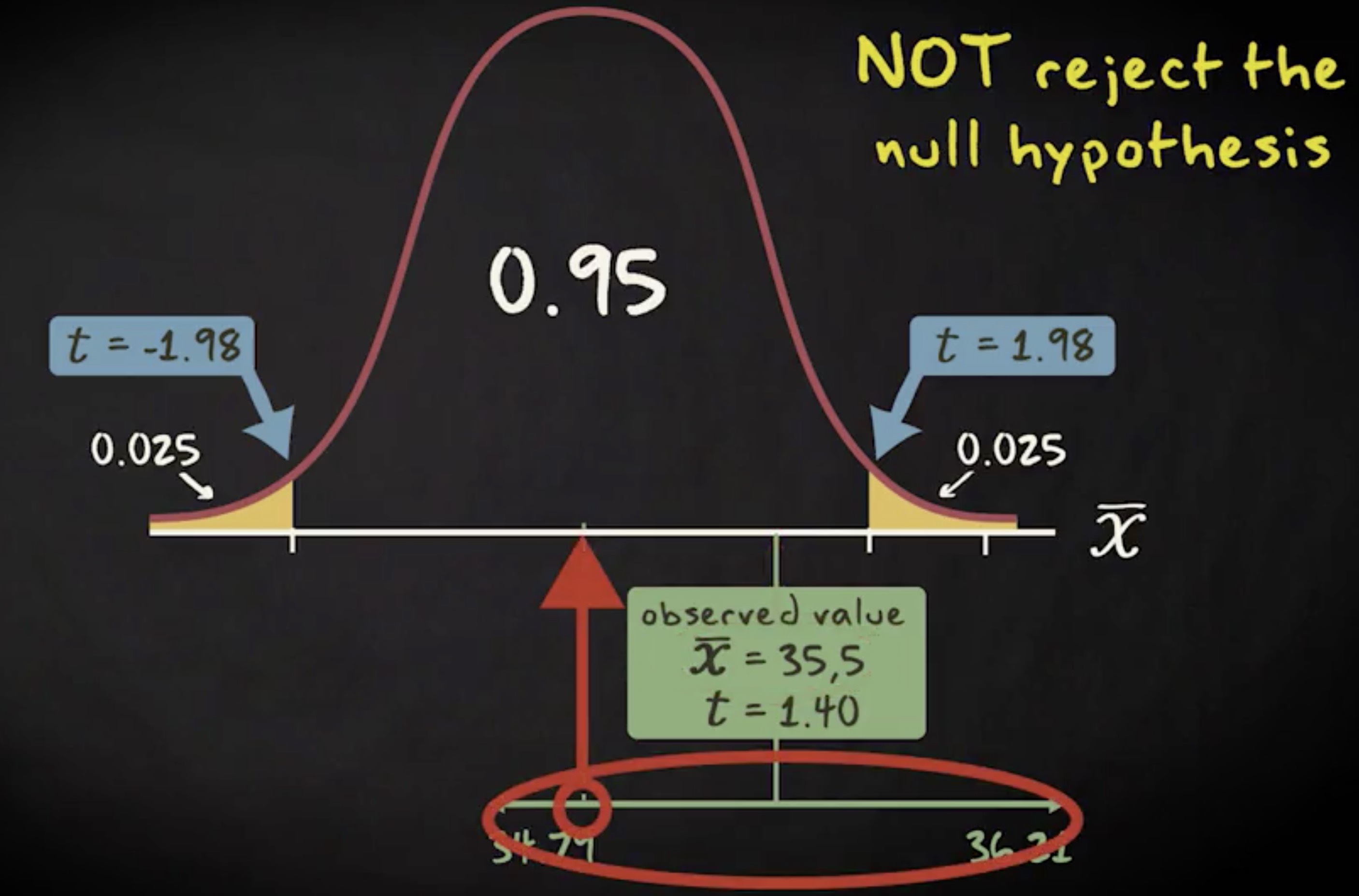
如果预期结果只出现了一次，或出现次数极少，那这个结果可能只是巧合。如果一个假说能被重复确认，它会更为可靠。所以一项研究需要经受住重复和复制的考验。比如我说服未婚夫认同 “猫在谁腿上呆得久就更喜欢谁” 这个评判标准。现在我观察到这周猫趴在我腿上的时间，是它呆在未婚夫腿上时间的两倍。那意味着我的假说是正确的吗？猫咪就爱我多一点吗？如果接下来几周这个观察结果保持不变，那么我的假说就是靠谱的。但如果观察了一周这只猫就死了怎么办？如此一来我们就无法验证这个假说了，这个研究再也无法重复。

要验证结果是否可重复，我们必须按原研究的条件和过程进行重复。假如我们处理过程不同，于是得到了别的结果，这表明原研究不可重复吗？答案当然是否定的。重复失败可能是由于我们改变了程序。

第三原则是 客观性 (objectivity) ，指他人能自行重复该实验而无需求助原研究者。“客观” 的字面意思是谁来进行研究不重要。基于假说跟其程序的描述，每个人都应该得到相同的结论。因此研究者提出的假说、概念、程序应尽量客观。这要求清楚明确地定义所有研究元素，不给主观解释留任何余地。

假设我认为猫咪拿脸蹭我是示爱的表现，但我没有明确告诉我未婚夫这一条，那么我衡量爱意的程序就是主观的。即使我们同时对猫进行系统性观察，结果仍然会因观察者而异。较之我未婚夫，我会认为猫示爱次数更多。这个例子中的结论是主观的，因此不具有可比性，而我们经常对此毫无自觉。如果我们没有明确讨论并就示爱标志达成共识，那么我们的猫咪爱意衡量程序则不够客观。

第四原则是 透明性 (transparency) 。保持透明度与客观性原则密切相关。在科学界，不论是你的支持者还是批评者，任何人都应该可以重复得出你的结论。这要求研究者共享他们建立的假设 —— 如何定义概念、使用了什么研究程序，还有一切和进行精确复制相关的所有信息。

第五原则指出一个假说应该具有 可证伪性 。可证伪性是一个非常重要的原则。如果你能想象出一种情形会使观察与假说出现矛盾，那么它就是可证伪的。如果我们想不出有什么样的反例存在，那这个假说就不可能被推翻。

比如你问一个有坚定宗教信仰的人，有什么证据可以证明他们的信仰是虚假的？不管你提出什么样的反例，他们可能都要争辩。这些事实并不违背自己的忠诚信仰。这种仅源于纯信念的观点，比如宗教，是不属于科学范畴的。如果对任何形式的证据，该假说都不接受其为反例，那这个假说根本没有讨论意义，也不用再寻求证实，因为结论已经在那里了。

我们要讲的第六点也是最后的原则是 逻辑一致性 (logical consistency) 。一个假说应该保持逻辑上的一致或连贯。这是指假说不会有任何自相矛盾的地方。比如 ，一个支撑假说的子假设是否与假说冲突。

我们观察得出的结论也应该保持逻辑一致性。这就是说，在整个过程中，研究者对正面或反面证据的标准应该一致。

让我继续用猫的例子进行说明。我的假说是猫更爱我，所以预测他会在我腿上呆更久。但要是它趴在我未婚夫腿上更久呢？我会说猫能察觉到趴在我腿上让我不舒服，因为他爱我多一些所以照顾我情绪便趴得少了。显然，这就是逻辑不一致。为了让观察结果符合我的假说，我对观察结果进行了 “再解读”。顺便一提，这也会让我的假说无法证伪。不管猫是否常趴我腿上，我都会得出它爱我的结论。

总结一下，科学方法要求我们构造的假说为实证可检验的，这就是说观察结果可以支撑或反驳假说；可重复性，也就是假说是可以被重复测试的；客观性，指他人可以独立检验这个假说；透明性，指假说与结果都公之于人，以便他人检验；可证伪性，指找到反例的可能性是存在的。最后，逻辑一致性是指假说本身保持内在的一致性，支持或反驳假说的观察结论也应逻辑一致。

最后一点，科学方法只在态度端正的情况下才有效。为了提出更好的假说，研究者们应该对自己和他人的研究持批判态度，所以他们应该做到公开透明、乐于接受批判。如果别人有更好的解释，就放弃他们心爱的假说。如此，科学界才能像进化系统一样 —— 只有最合适、最可靠的假说存留下来。

科学主张 (Scientific Claims)

我已经讲过了有关我们周围世界的命题、假说以及解释，我没有准确解释就用了这些通用术语。是时候阐明清楚了。

关于周遭世界的科学主张，可分为不同类别。一些科学主张会比别的主张描述或解释更多现象。同样，某些科学主张对于我们周围的世界，命题、假说以及解释提供了更可信的描述或解释。我们发现某些主张会更准确一些，比起别的来有更多证据支持。

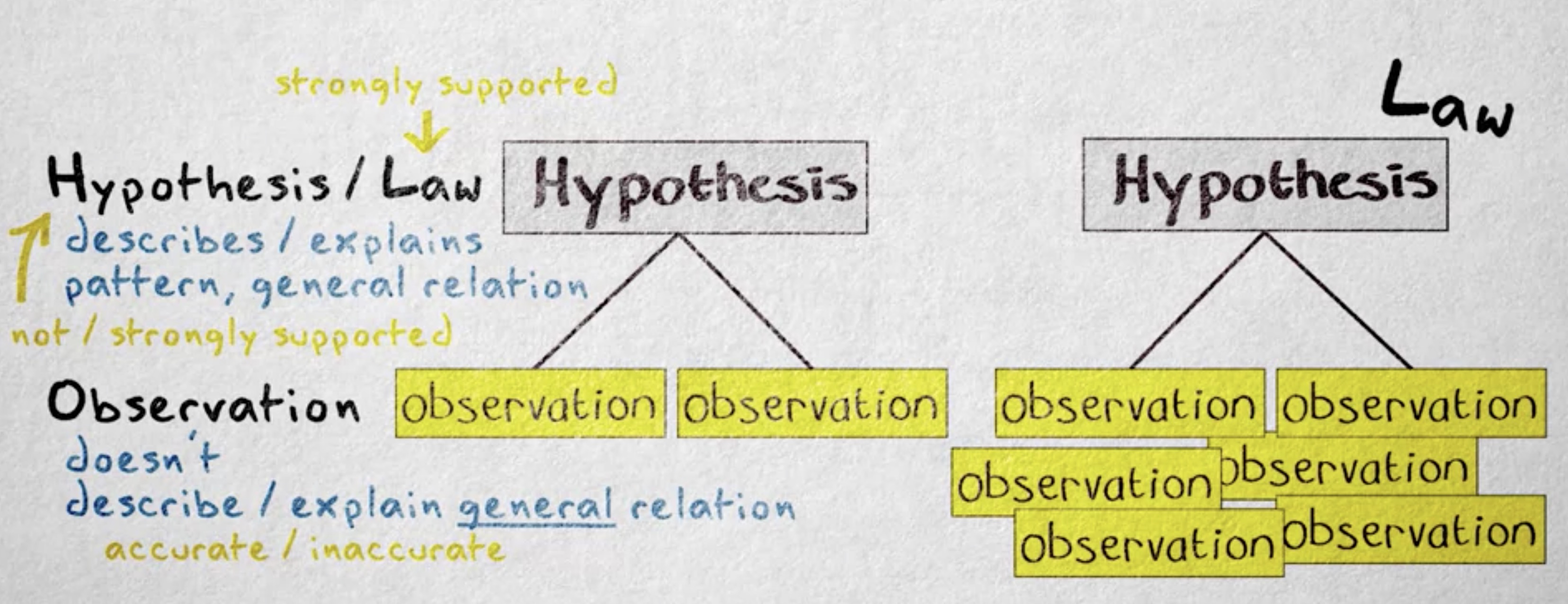
在科学中，最基本的主张是 观察 (observation) 。观察可以是对世界准确或不准确的 表达（(representation) 。

假设我观察我的猫：姜黄色毛，重 6.5 公斤。大多数科学家会接受这个观察结果，作为我们周围世界某一方面较为准确的投射 —— 假设体重秤有效且可靠的。但就解释力度而言，他们会发现这个观察非常无趣 —— 观察本身没有很大信息量，它不能描述属性间的一般联系，无法解释任何事。

但这不表示观察不重要。观察是经验科学的基础，但是观察本身不是很有用，观察本身是最无趣的科学主张，因为它没什么解释能力。观察在确定或反驳假说时会变得有用。

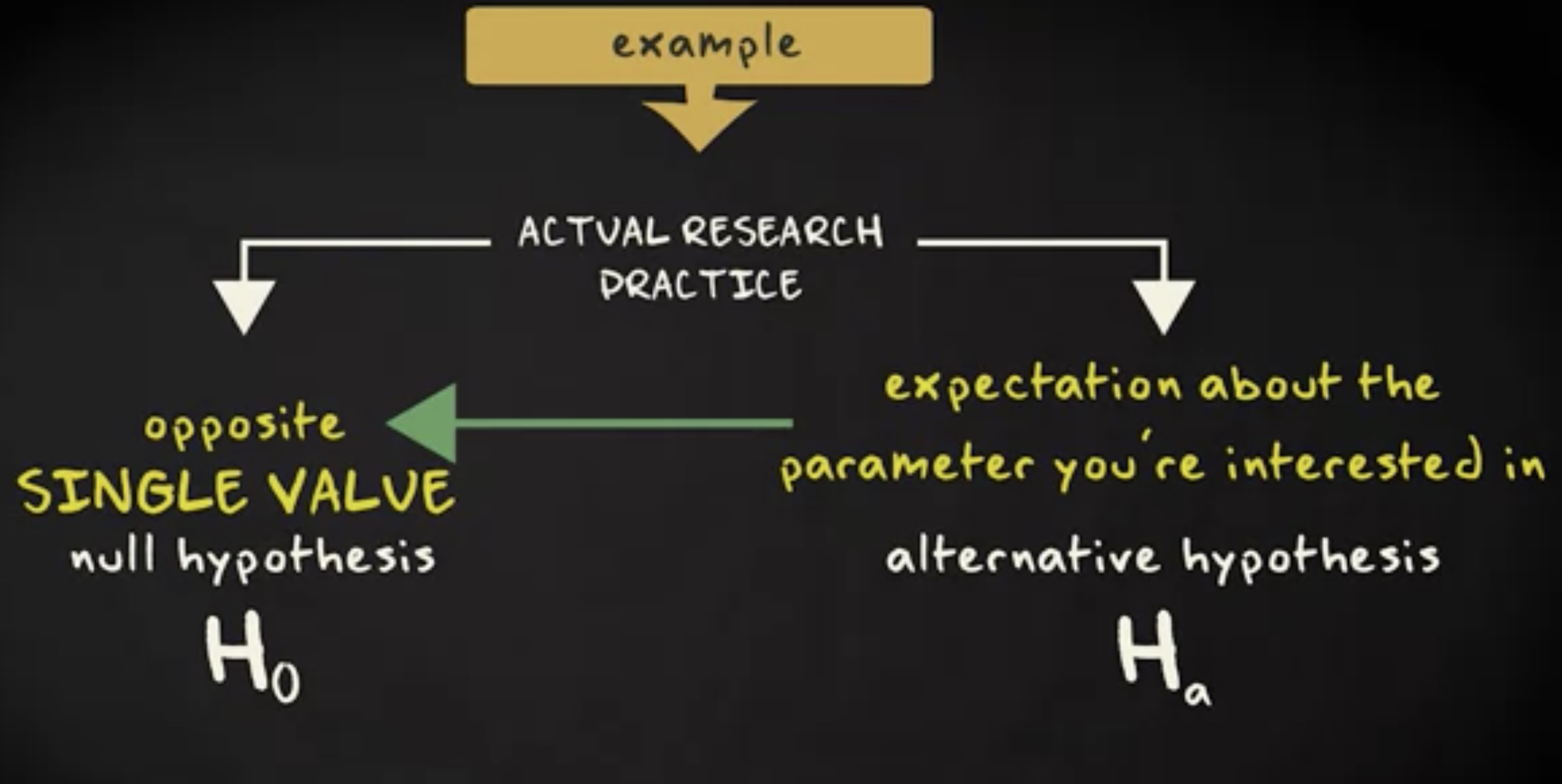
假说 (hypothesis) 是一种 命题 (hypothesis) ，它描述了 属性 (hypothesis) 间的 模式 (pattern) 或一般关系。假说也可以对它描述的模式进行解释。我们建立这样一个假说：姜黄色猫一般都会超重，概率比其他颜色的猫要高得多。我可以用解释来延伸这个假说，就是毛色和肥胖间的相关性。比如，通过证明控制姜黄毛色和发出饱腹信号的基因是连锁的。

假说的 可信度范围 (plausibility) 可以从非常不确定到非常确定。一个假说若是没有支持，那么它就是不确定的。比如这是个新且未经检验的假说。假说也能被很多实证研究强烈支持，从而变得更确定。

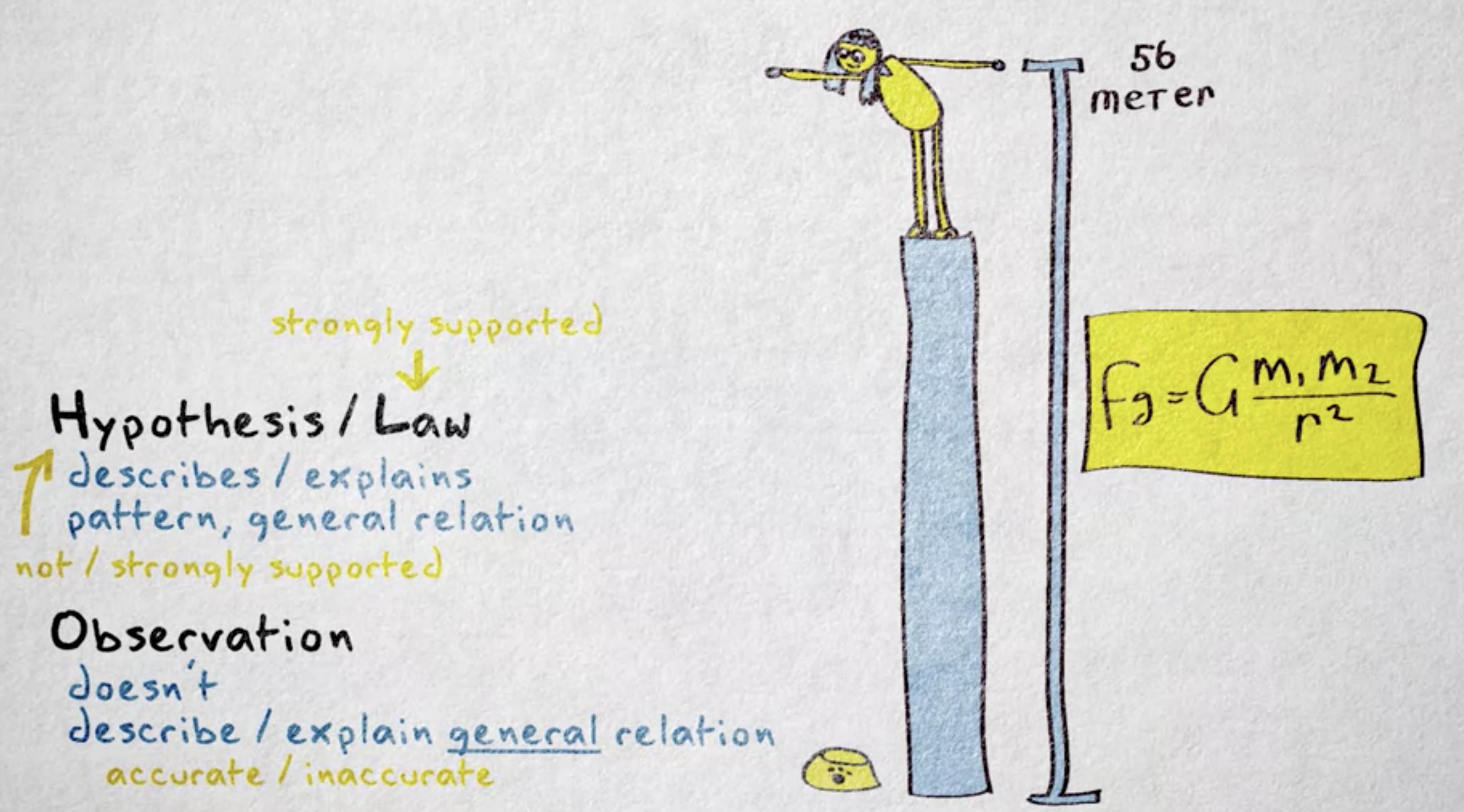
假设的一种特殊类型就是 定律 (law) ，定律是对 关系 (relation) 或模式非常精确的描述 —— 精确到总是能用 数学公式 (mathematical equations) 表达。它们通常被证明得很完整，所以它们如此精确。比如，我把猫食盆从 56 米高的地方扔下去，且我知道万有引力常数，然后用牛顿的万有引力定律就能很准确地预测这个碗掉到地上要花多长时间。

定律能做出很精确的预测 但它们通常不会解释其描述的关系。在这里，是距离、时间和重力之间的关系。当然，社会科学方面的定律很少能表达成公式。我们对个人和人群的了解还太少，还不能得到如此精度的固定行为模式，并用来推测出科学定律。

好，接下来我们来讲讲 “理论 (theory)” 的概念。在日常生活中，理论意味着 未被证明的 (unsubstantiated) 命题，有根据的猜想。但是在科学中，理论指的是许多相关现象的总体解释。在自然和行为科学中，理论由被经验证据强烈支持的各种假说构成。在社会科学中，更多的是定性研究和历史比较的方法。当理论经受住了逻辑上、历史上或定性分析的驳斥时，可以认为该理论高度可信。

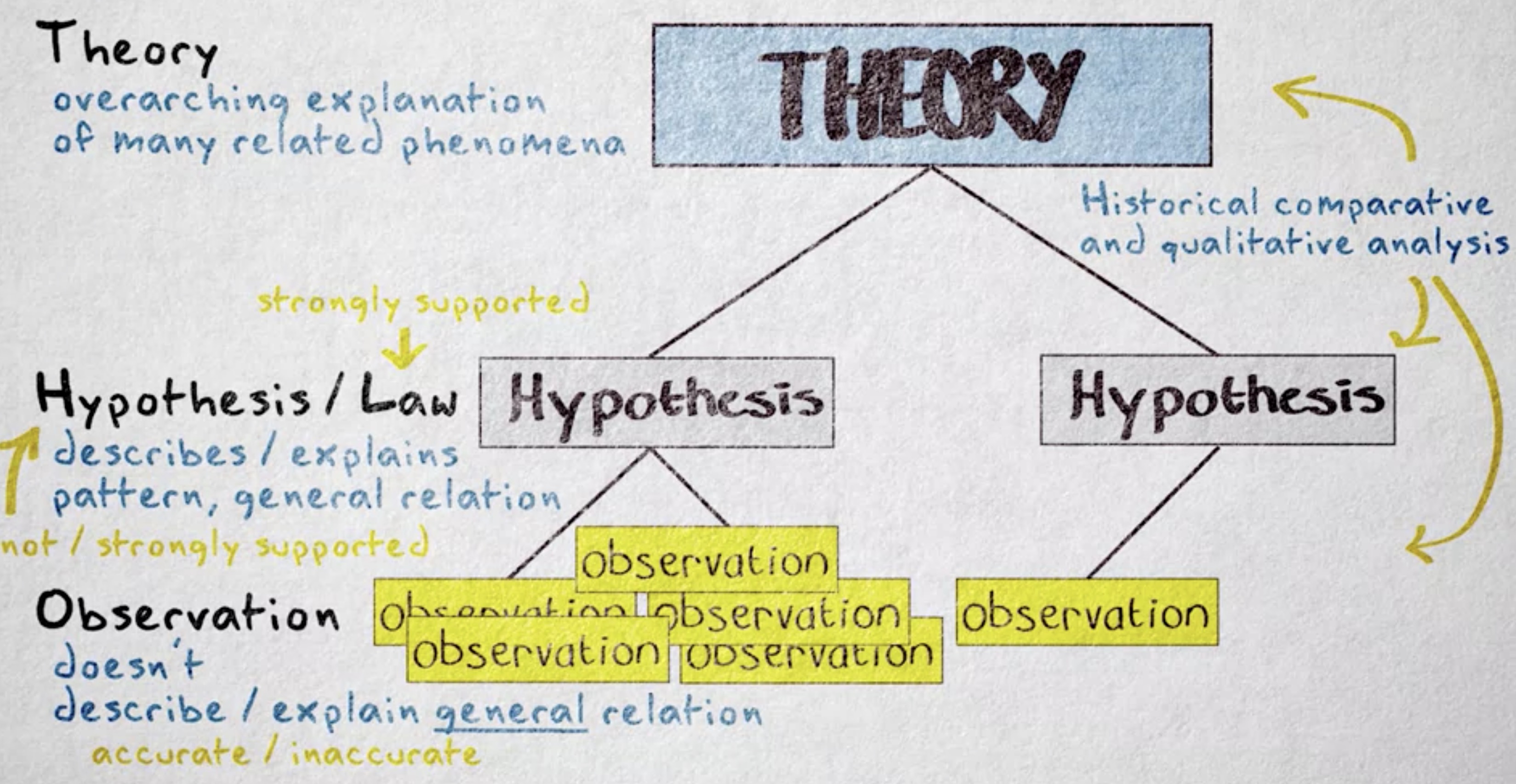
在科学范畴里，理论的解释最为完善，是我们拥有的最接近准确的东西，因为它们由经科学方法审视并留存的假说构成。当然，这不意味着科学理论是确定或真实的。世上有许多证明完备的理论最终也被取代了，比如牛顿力学就为相对论让路了。 科学的世界里没有确定性，只有暂时的最佳解释 (provisional best explanation)。

欢迎关注微信公众号「Swift 花园」

第一类错误和第二类错误

回忆一下此前提到过的庭审的例子。被告方的辩护律师的观点是被告是无辜的，公诉方则试图说服陪审团和法官被告是有罪的。举证有罪的责任在于原告。被告只有在原告提供有力证据驳斥被告假定无罪的情况下才能被认定为有罪。

在审判时，有四种可能的结果。一，被告确实有罪且被判有罪，这是个正确的决定。二，被告确实无辜且被判无罪，这也是正确的决定。三，被告实际上是无辜的，但被判有罪，这是错误的决定。四，被告实际上有罪的，但是被判无罪，这也是错误的决定。

这也是我们在实施显著性检验时会发生的情况。辩方观点类似零假设为真，而被告有罪则等效于零假设为假。判被告有罪类似拒绝零假设，而无罪释放则等同于不拒绝零假设。这会导致四种可能的情形。其中的两种，你做了正确的决定，包括零假设的确为真并且你没有拒绝它以及零假设的确为假并且你拒绝了它。但也有两种你做了错误的决定，包括零假设为真而你拒绝了它以及零假设的确为假而你没有拒绝它。第一个错误我们称为 第一类错误 (type I error) ，或者说 伪阳性 (false positive) 。第个错误我们称为 第二类错误 (type II error) ，或者说 伪阴性 (false negative) 。

让我给你举个例子。想象你的零假设是：美国的持证水肺潜水者总体， 50% 有超过 35 小时的潜水经验。换言之， $ \pi = 0.5 $ 。备选假设是它是另外一个百分比，换言之， $ \pi \neq 0.5 $ 。你问了一组简单随机抽样的 500 个美国潜水者，你发现有 0.56 的比例有超过 35 小时的潜水经验。现在，假定你的零假设实际上是真的，当你决定基于你的样本数据拒绝零假设时，一个第一类错误就出现了。

欢迎关注微信公众号「Swift 花园」

分步计划

比较以下两种期望。一，你期望超过半数的持证美国潜水者有超过 35 小时的潜水经验。二，所有持证美国潜水者的平均潜水时长超过 35 小时。第一眼，两个期望看起来很相似。但是，在第一个例子中，你面对的是比例，你感兴趣的是潜水经验超过 35 小时的潜水者的比例。而第二个例子中，你关心的是均值。你想知道潜水时长的均值。因此，当实施显著性检验时，你需要特别注意你的方法。

这一节中，我将以分布计划的方式来引导你。想象你问了一个容量是 500 个持证潜水者的简单随机样本，他们的潜水时长是多少个小时。假设你发现 0.57 的比例有超过 35 小时的潜水经验，时长均值是 35.5 小时，均值是 8 小时。在我们的样本中，
潜水经验的变量分布近似正态。下面是分布计划全图：

第一步，评估你面对的是比例还是均值，这个我们已经讨论过。第一个例子是比例，第二个例子是均值。

第二步，形式化你的假设。在比例的例子中，零假设是：$ \pi = \pi_0 $ ，在均值的例子中，零假设是 $ \mu = \mu_0 $ 。我们可以有三种类型的备选假设：如果你做双尾检验，是 $ \pi\neq\pi_0 $ 或者 $ \mu\neq\mu_0 $ ；如果你做单尾的右尾检验，是 $ \pi\geq\pi_0 $ 或者 $ \mu\geq\mu_0 $ ；如果你做单尾的左尾检验，是 $ \pi\leq\pi_0 $ ，$ \mu\leq\mu_0 $ 。我们零假设是： $ \pi=0.5,\mu=35 $ ，备选假设是 $ \pi\geq0.5,\mu\geq35 $ 。因此我们需要实施右尾检验。

第三步，检查你的假定是否满足。在两个例子中，随机化都是必要的。你的样本必须通过随机抽样的方法收集，或者说，随机化的实验。在比例的例子中，根据零假设的比例，样本容量乘以比例以及 1 减去样本容量再乘以比例，必须等于或者大于 15 。均值的例子则要求总体分布近似正态。但实践中，这一点只有样本容量很小，且做的是单尾检验时才重要。对于我们的例子，所有的假定都满足。

第四步，确定显著性水平 $ \alpha $ 。常用的显著性水平是 0.05 。我们的检验将基于 $ \alpha=0.05 $ 。

第五步，计算检验统计量。在比例的例子中，公式是 $ z = \frac {p-\pi_0}{se_0} , se_0 = \sqrt {\frac {\pi_0 (1-\pi_0)}{n}} $ ，在均值的例子中，公式是 $ t = \frac {\bar x-\mu_0}{se_0} , se_0 = \frac {s}{n} $ 。注意，在比例的案例中，我们使用 z 分布，而在均值的案例中，我们使用 t 分布。

第六步，抽取相关的抽样分布，展示零假设和检验统计量，补上拒绝域和对应的临界值。在比例的案例中，

第七步，评估你的检验统计量是否落在拒绝域内。

第八步，决定是否拒绝零假设。

第九步，解释你的发现。

在下结论之前，值得提醒的是，不拒绝零值假设并不暗含你就可以接受零值假设。在第二个例子中，我们不拒绝零值假设，即潜水时长等于 35 小时的假设，但并不能得出潜水时长就等于 35 小时的结论。

显著性检验和置信区间

假设你问样本容量为 500 的水肺潜水者他们潜水了多少个小时，均值是 36 小时，标准差是 8 小时，变量的样本分布近似于正态。基于样本信息，你希望推断总体的参数 $ \mu $ ，这是我们所知的推断统计学 —— 基于样本信息得出样本所在总体的结论。

推断统计学有两种方法。其一，通过均值的置信区间来推断区间估计。其二，用显著性检验来推断点估计。在这一节中，我将向你展示这两种方法其实关联密切。

假定你预期潜水时长的均值不是 35 小时，你将做一个显著性检验。我们对均值感兴趣，检验统计量如下：

零假设是： $ \mu = 35 $ ，备选假设是： $ \mu \neq 35 $ 。我们的假定满足，分析基于简单随机样本并且样本足够大，并且样本近似正态分布。检验统计量等于 36 减去 35 ，除以 8 除以 500 的平方根，等于 2.80 。抽样分布看起来是这样的。

我们可以通过查询 t 表找到对应双尾检验显著性水平 0.05 的临界点是 $ \pm1.984 $ 。因此我们的检验统计量落在拒绝域内。我们将拒绝零假设，得出潜水时长不等于 35 小时的结论。

现在，如果我们构造 95% 的置信区间，会发生什么呢？公式如下：样本均值，加减 95% 置信水平对应的 t 分数，乘以标准误差，这个标准误差等于标准差除以样本容量的平方根。相关的 t 分数是 1.984 ，代入公式，得到置信区间是 35.29 到 36.71 。由此我们有信心说，通过无限重复的抽样， 95% 的情况下区间会包含实际的总体均值。这个区间给了我们关于总体均值的一个有说服力的范围。和显著性测试一样，这个置信区间也告诉我们，总体的样本均值不是 35 。通常，双尾显著性检验的结果与置信区间的结果是一致的。

更准确的说，如果双尾显著性检验的 P 值等于或者小于 0.05 ，那么 95% 置信区间也不包含零假设的值。类似的，如果双尾检验的 P 值大于 0.05 ，那么 95% 置信区间将包含零假设的值。

这听起来很合理，对吧？它以下图表示。你会看到，观察值 36 落在拒绝域内，而对应的置信区间也不包含零假设的总体均值。

现在假设观察到的均值是 35.5 ，而不是 36 ，这样的话，我们的检验统计量将变成 1.40 ，它不落在拒绝域内。我们因此不拒绝零假设，相似的，置信区间的两个端点编程 34.79 和 36.21 ，则包含了零假设的均值 35 。

我们可以有信息说，通过无限重复抽样， 95% 的情况区间会包含实际的总体均值。这意味着零假设有说服力，我们不该拒绝零假设。也说明了，构建置信区间的方法和双尾假设检验的方法虽然看起来不同，但是数学上是相关的，彼此一致。

欢迎关注微信公众号「Swift 花园」

假设

教程来到最后一个模块，很快我要放假了。明天我将背起行囊，出发去潜水。好吧，让我们再谨慎一点，我并不完全确定明天我能成行。我的航班可能延误，我可能睡过头误了航班，或者可能生病导致无法去潜水。总之，我期望明天出发，但我并不能完全地确定。或者说，不能 100% 确定。

当研究人员对于他们感兴趣的参数有所期待时，我们在讨论的是 统计假设 (statistical hypotheses) 。这一节将介绍统计假设。他们构成了 显著性检验 (significance testing) 方法中最主要的部分。一个统计假设，其实就是一个关于总体的期望。通常，假设会被形式化为一条对总体参数持有特定值或者落在特定范围的声明。这种声明是基于研究或者理论。基于样本的信息，我们评价一个假设靠谱与否。这个过程我们称为显著性检验，它是一种用样本数据来检验提前形式化的假设的方法。就像置信区间一样，显著性检验是一种推断统计学的方法。毕竟，我们也是用样本数据来推断关于总体参数的结论。

我们先来看 零假设检验 (null-hypothesis testing) ，在这种检验中，显著性检验基于两个假设， 零假设 (null hypothesis) 和 备选假设 (alternative hypothesis) 。零假设以 $ H_0 $ 注记，备选假设以 $ H_a $ 注记。零假设断言你感兴趣的参数是某个特定值。它通常代表变量之间没有关联的情况，或者组与组之间没有差异的情况。它是一个当你的样本数据表明它不太可能发生时需要被拒绝的假设。而备选假设断言你感兴趣的参数落在另一个范围。通常，零假设和备选假设互斥。如果你做显著性测试，假设零假设为真，除非你的数据有很强的反面证据。

想象一个法庭的庭审。被告方的辩护律师的观点是被告是无辜的，公诉方则试图说服陪审团和法官被告是有罪的。举证有罪的责任在于原告。被告只有在原告提供有力证据驳斥被告假定无罪的情况下才能被认定为有罪。这正是显著性检验里发生的事情。辩护无辜相当于零假设，而有罪预期则等同于备选假设。

在研究实践中，你对于参数的期望是以备选假设的方式出现，而零假设就是对立面，但它必须是一个单值，不能是一个范围。你只有在数据提供强力佐证时才能认定零假设成立。

欢迎关注微信公众号「Swift 花园」

还是前面的新生儿父母睡觉减少时长的例子，由于我们无法去询问你家乡所有的年轻父母。我们采取简单随机抽样。一个很关键的问题是 —— 样本应该取多大。应该是 50 个就够了？或者 至少 300 个或者 1000 个？

这一节中，我们将分布讨论对均值和比例感兴趣的不同情况。

先从均值开始。样本容量主要取决于三个因素。首先是你想要的精度。记得吗，置信区间是通过点估计加减一个误差界限来得到的。你允许多大的误差界限，如果你希望它越小，那么你的样本容量就得越大。其次，你的样本容量还依赖你想要的置信水平。越大的置信水平，需要越大的样本容量。最后，数据的变异性也影响样本容量的选择。你的变量的标准差越大，你需要的样本容量也越大。公式如下：

n 代表样本容量，m 代表误差界限，$ \sigma $ 代表总体的标准差， z 代表 z 分数。显而易见，你不知道总体的标准差，而且你还没抽取样本也不知道样本的标准差。所以，你需要利用 合理的猜测 (educated guess) 来估计一个值。

让我来演示这个过程是怎么样的。想象我们想要 95% 的置信水平，对应这个置信水平的 z 分数是 1.96 ，并且我不希望误差界限宽过 0.3 小时，就取 0.3 小时吧。现在我们可以填完这个公式的一部分了。现在我们需要对 $ \sigma $ 进行合理猜测了。如果已经存在这方面的研究而且你知道变量的标准差，可以简单地采纳这个标准差。但是，如果这样一个研究之前并未做过，就必须靠我们自己的猜测。我先假定某些父母根本没法睡，某些父母睡觉少于 5 个小时，并且父母们也不可能睡的比之前还多。因此，我们假定变量服从正态分布， 95% 的父母睡觉时间介于 0 到 5 个小时之间。均值是 2.5 小时，标准差是 1.25 小时。毕竟， 95% 是落在均值左右两个标准差范围内，两个标准差等于 2.5 ，那么一个标准差就是 1.25 。我们用这组数字完成公式，得到 66.69 ，取整，得出结论我们需要 67 个受试者。

对于比例感兴趣而不是均值的情况，也可以采取类似的方式。假设我们想知道新生儿在换尿布时便便的比例，我想要 99% 的置信水平，误差界限 0.10 。公式非常相似：

m 是 0.10 ，z 可由查表得 2.58 ，它对应 99% 置信水平。我们不知道的是 p 。还是采用合理的猜测，或者采用一种被称为 安全方法 (safe approach) 的方式。你会发现 $ p (1-p) $ 的最大值是 0.25 ，它发生在 p = 0.5 的时候，于是我们用 p = 0.5 完成公式，0.5 乘以 0.5 乘以 2.58 的平方除以 0.10 的平方，得到 166.41 ，即 167 位受试者。

在理想世界中，你可以去寻求大样本，比如说 1000 位受试者或者更多。但是，在现实世界中，我们的时间有限，资源有限，无法抽取大样本。因此，计算所需的样本容量可以帮助我们把成本降到最低。