欢迎关注微信公众号「Swift 花园」

比例的置信区间

在过去的几周中我认识到新生儿喜欢排便，频繁地排便。恰好我的女儿 Lois 尤其喜欢在特定的情况下排便 —— 在我给她换尿布的时候。我说真的，一旦她决定上厕所 (answer nature’s call) ，一上就是六次。是的，六次，发生在换尿布的过程中。

这正常吗？我不确定，但我知道我需要搞清楚。假定我随机问 100 个新生儿的父母，他们的宝宝是否喜欢在换尿布时排便。在这一节教程中，我会告诉你，如何基于这样一个研究，构建一个估计总体比例的置信区间。

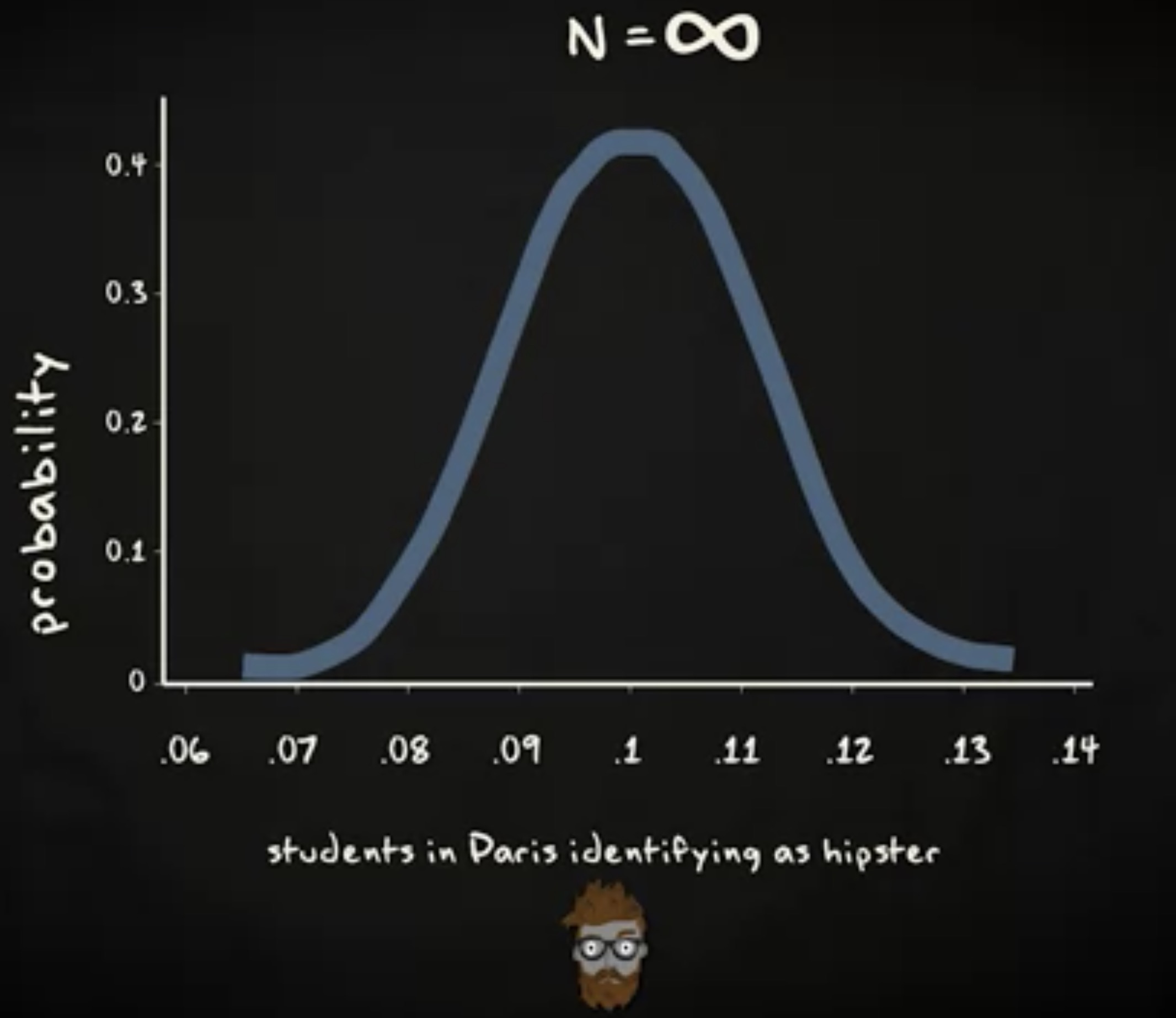
假定我的 100 的受试者里有 17% 报告他们的宝宝喜欢在换尿布时排便， 83% 的受试者报告他们的宝宝不会这样做。我们由此得到一个 0.17 的比例，这个比例的新生儿父母的宝宝喜欢在换尿布时排便。当我们为比例构建置信区间时，我们引入样本比例的抽样分布。我们知道，只要样本足够大，这个抽样分布就是正态分布，并且均值等于总体比例 $\pi$ ，标准差 $\sigmap$ 等于 $ \sqrt {\frac {\pi (1-\pi)}{n}} $ 。我们还知道，找到一个比例处于均值两个标准差范围内的样本的概率，同时也是总体的比例，是 0.95 。 更精确的说，如果我们对应概率的 z 分数，我们会得到 1.96 。这意味着我们有 95% 的机会确定我们的样本比例会落在总体比例 1.96 个标准差范围内，这被我们称为 _误差界限 (margin of error) 。我们用于计算 95% 置信区间的公式如下：

$$p\pm1.96\sigma_p , \sigma_p = \sqrt {\frac {\pi (1-\pi)}{n}}$$

其中 1.96 是对应 95% 置信区间的 z 分数。所以上面的公式我们也可以写成：

$$p\pm {Z_{95\%}}\sigma_p , \sigma_p = \sqrt {\frac {\pi (1-\pi)}{n}}$$

我们这里讨论的是 95% 的置信区间，意味着如果我们能从总体抽取无限多的样本，那么 95% 的情况下，我们的置信区间会包含总体比例 $\pi$ 。不过，你可能注意到，我们并不知道总体比例 $\pi$ 的值，所以就无从计算样本比例的抽样分布的标准差。因此，我们用一个估计值来代替总体参数 $\pi$ ，这个估计值来自样本统计量， $P$ ，由此得到下面的公式：

$$p\pm {Z_{95\%}}(se) , se = \sqrt {\frac {p (1-p)}{n}}$$

就像我们为均值构建置信区间时一样，我们称这个估计的标准差为 标准误差 (standard error) ，又称为标准误。 作为与均值的置信区间的对比，在构建比例的置信区间时，我们并不使用 t 分布。不过，你的数据需要满足一个必要的假定。你必须要有至少 15 个成功和 15 个失败。换言之， $np \geq 15$ 并且 $n (1-p) \geq 15$ 。如果不满足，那 你就不能基于上面的公式计算置信区间。现在回到例子，我们有 0.17 的比例报告宝宝在换尿布时排便。公式如下：

$$p\pm {Z_{95\%}}(se) , se = \sqrt {\frac {p (1-p)}{n}}$$

让我们先计算标准误差。0.17 乘以 0.83 ，除以 100 ，然后取平方根，结果是 0.038 。误差界限等于 1.96 乘以 0.038 ，约定于 0.07 。 0.17 减去 0.07 等于 0.10 ，0.17 加上 0.07 等于 0.24 。因此我们的置信区间是 0.10 到 0.24 。这意味着我们有 95% 的信心说，总体比例落在 0.10 到 0.24 之间。或者说，如果我们能抽取无限多容量为 100 的样本，那么对于每个样本我们计算这个误差界限下的置信区间，有 95% 的情况这个区间会包含总体的比例。这个 95% 置信区间说明，大部分宝宝并不喜欢在换尿布时排便。但另一方面，如果他们确实在这个时候排便了，也并奇怪。我们有 95% 的信心说有 10% 到 24% 的宝宝确实会在换尿布时排便。

---

置信水平

95% 的置信区间，告诉我们对于我们的点估计有 95% 的可信度，这个点估计可以是均值或者比例。或者说，如果能够抽取无限多的样本，近似于我们当前的样本，对所有的样本基于相同的误差界限计算 95% 的置信区间。那么 95% 的情况下，总体的参数值回落在这个置信区间内。同时也意味着， 5% 的情况，这个方法会产生一个不包含实际总体参数的区间。

如果你希望减少错误推断的可能性，你可以诉诸更大的置信区间，比如说 99% 。这一节中，我将向你演示如何改变置信水平，以及这么做会带来什么结果。

99% 置信区间和 95% 置信区间的唯一区别是不同的 z 分数，通过查询 z 表，代入公式，最终我们算得 99% 置信区间是 0.07 到 0.27 。对于 90% 的置信区间，结果是 0.11 到 0.23 。

我以图形演示，你会看到，更高的置信水平导致更宽的置信区间。换言之，我们想获得可信度越高的推断，那么就要接受更宽的误差界限。因此，我们需要在可信度和精度之间折中。在多数情况下，我们采用 95% 置信区间。

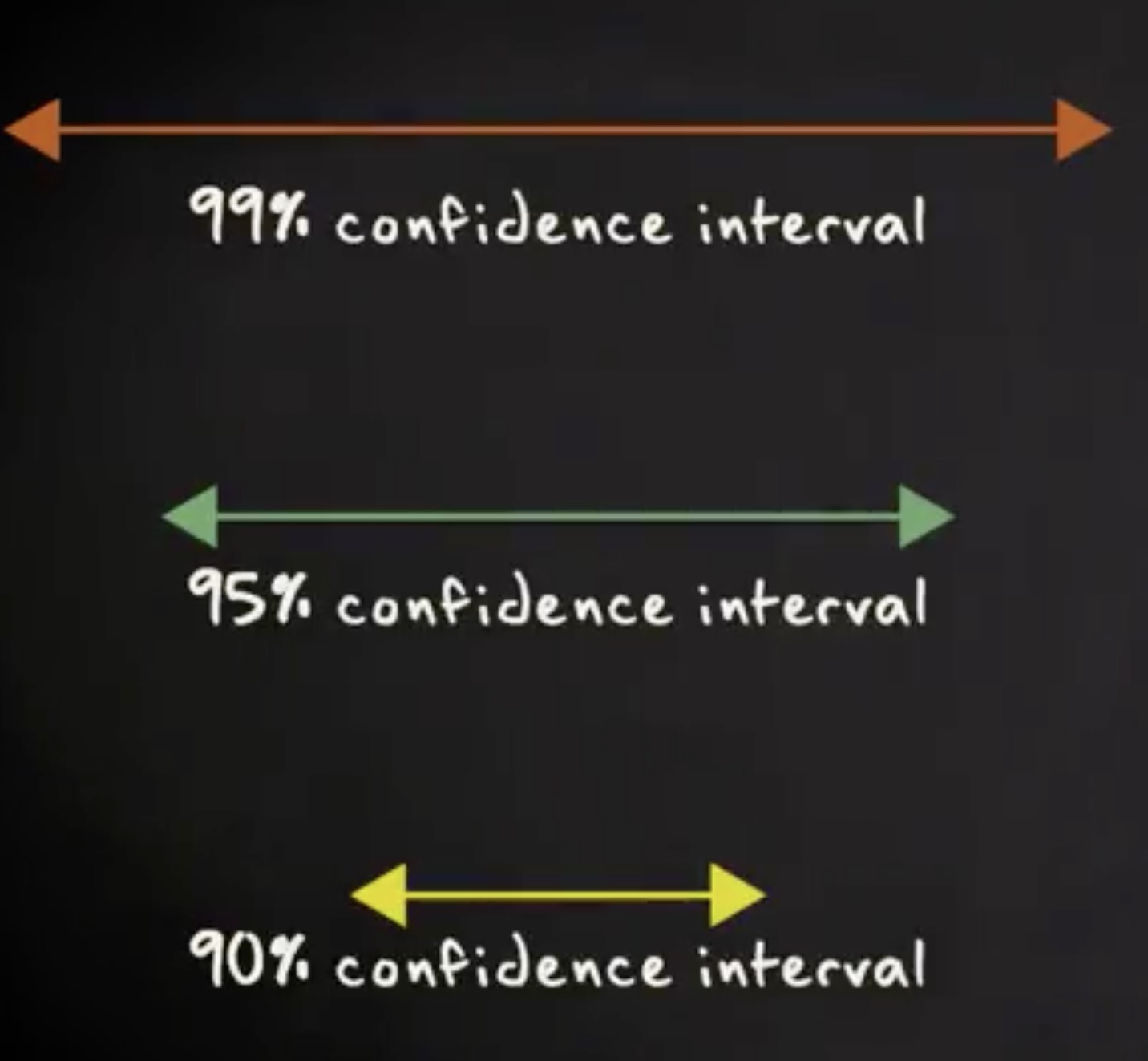
这个原理同样适用于均值的置信区间，区别在于在比例中，我们查询相关的 z 分数而在均值的案例中，我们查询相关的 t 分数，并且均值的计算中还要用到自由度，即 n 减去 1 。

---

欢迎关注微信公众号「Swift 花园」

统计推断

这一节我们以睡眠为例。假设你通常每晚睡 8 个小时，你突然做了年轻爸爸或者年轻妈妈，你的睡眠时间减少到每晚 5 个小时，这意味着每晚减少 3 个小时，相当于每周 20 个小时，每年 1000 个小时，差不多 40 天。换言之，如果你家宝宝继续保持他 / 她的睡眠时间，一年之后你会比之前少睡 大约 40 天。

回到统计学，想象你想要知道你家乡的年轻父母在孩子刚出生那一年减少了多少睡眠。在这一节中我们将讨论统计推断。我们会基于样本信息，得出关于总体的结论。我们将会区分两种统计推断的方法，一种叫 统计估计 (statistical estimation) ，另一种叫 假设检验 (hypothesis testing) 。在这篇教程中，我们将先了解统计估计。

有两种方式估计总体参数的值，其一叫 点估计 (point estimate) ，它是一个对于总体参数的最佳猜想。其二是 区间估计 (interval estimate) ，它是一个我们预期参数会落在的范围。

想象我们抽取了 60 个受试者样本，有了第一个小孩后每晚减少的睡眠小时数均值为 2.6 小时。这个均值是一个对于总体均值很好的点估计。换言之，$ \bar x $ ，是一个对于 $ \mu $ 的很好的点估计。不过，单一的点估计无法告诉我们估计是否接近我们感兴趣的总体参数。因此，研究人员通常还希望知道点估计可能的准确度。他们借由计算区间估计来显示这种准确度。

区间估计是一个最有可能包含总体实际参数值的数字区间。基于我们的样本均值 2.6 小时，我们可以预测，比如说，你家乡新生儿父母每晚睡眠减少的平均小时数介于 2.3 小时到 2.9 小时之间。

这个区间包含总体参数值的概率，被我们称为 置信水平 (confidence level) ，置信水平总是一个接近 1 的值，多数情况下是 0.95 。接下来我们将讨论有 95% 置信水平的区间。

欢迎关注微信公众号「Swift 花园」

抽样分布比例

想象你住在巴黎，你知道所有的学生中有 0.10 的比例把自己看做嬉皮士。你想要知道这个比例的抽样分布是什么样的。注意，在这里计算总体均值是没有什么意义的。因为你感兴趣的变量是一个二元标量。学生们可以选择认定自己是或者不是嬉皮士。均值和这样一个二元变量无关。

在本节教程中，我将解释一个总体比例的抽样分布是长什么样。你知道巴黎有 10% 的学生认为自己是嬉皮士，这意味着总体比例，用 $ \pi $ 注记，等于 0.10 。现在想象我们从这个总体中抽取 200 个学生。样本的比例，用 $ p $ 注记，将会是一个接近 0.10 的数字，比如 0.09 或者 0.12 。

如果抽取了 5 组样本，样本比例可能如下：

这样样本比例的直方图可能如下：

有五个值，全部都出现一次，它们的概率都是 0.2 。现在，你抽取 25 组样本，分布可能如下：

抽取 50 个样本，分布如下：

无限多组样本，分布如下：

这是样本比例的抽样分布，分布的均值是 0.10 ，等于总体的比例。为了表明我们是处理抽样分布的均值，均值被注记为 $ \mu_p $ ，下标 p 是为了说明我们正在处理的分布的分数不是个体的分数，而是样本比例。如你所见，逻辑上和样本均值的抽样分布一模一样。

欢迎关注微信公众号「Swift 花园」

抽样分布

研究人员经常会用样本来推断样本所处的总体。为了做这件事，他们需要用到统计世界中非常重要的一种概率分布 —— 抽样分布 (sampling distribution) 。

这一节中，我将向你解释抽样分布是什么。需要特别注意的是，抽样分布是帮助研究人员基于仅仅一个样本得出关于总体结论的桥梁。另外说明，在这节教程中，我们假装自己知道总体是什么样的。因为在研究实践中，我们通过永远都无法得知总体的全貌。这一步对于理解推断统计学至关重要。

好吧，让我们进入正题。想象有一群北欧的嬉皮士组织了一场胡子节庆典。庆典将在挪威首都奥斯陆附近的一个小岛举行。显然，你能想到庆典的受众是有胡子的男性。组织售出了 5,000 张门票，并且提供了往来小岛的免费运送。

拥有门票的人将在奥斯陆的港口集结。组织将他们随即分装到运送乘客前往该岛的船上，每条船搭载 30 名庆典的粉丝。

现在，有一艘船迷失在挪威的群岛间。雪上加霜的是，手机网络崩溃了，因此组织无法联系上船长，船上的乘客也无法联系上组织。所有组织决定派出一些雇员去搜寻走失的船只。你正是其中的一名雇员。在历经里半个多小时的搜寻后，你看到一艘失事的船，上面有大约 30 个人。Yes，终于找到他们了。你正准备通过对讲机向组织报告失联船只已找到，这时你再看了一眼船上的乘客。你发现乘客都是一些带着小孩的家庭。这很奇怪，去胡子节的船上，不是应该都是一些随机选取的有胡子的成年男人吗？而不是一些带着小孩的年轻家庭。你认定这艘船不太可能是你要找的船，决定继续搜寻。果然，不久之后证明你的决定是明智的。你前面遇到的那艘船是一艘运送人们去另外一个岛上的家庭公园的船。

为什么要讲这个故事呢？这么说吧，如果你理解上面那个故事里 “你” 决策的原因，你就会理解抽样分布背后的基本思想。它是这样的，如果你从总体中抽取一个简单随机样本，那么它是不太可能强烈地区域于样本所处的总体的。在我们的案例中，人们正前往胡子节，他们构成了总体。一艘载有 30 个从总体中随机选取的人的船就是一个简单随机样本。

实际上，所有从奥斯陆港口前往庆典小岛的船都可以看做是一个简单随机样本。当然，每艘船都和其他船不一样，但大部分船都会包含大比例的有胡子的男人。不太可能有一艘船上都是各种年轻家庭。当然，有某些家庭参加胡子节是可能的，但是随机遇到一艘船，全部都是年轻家庭，则是非常不太可能发生的。

假设你决定测量每艘船的平均胡子长度。每艘船有 30 个人。想象 5,000 个庆典参与者的平均胡子长度时 10.3 毫米，即均值是 10.3 毫米。你还知道胡子的长度在总体中服从一个钟形的分布。在一艘船上，你可能遇到胡子平均长度是 9.4 毫米，另一艘则可能是 10.8 。但是，不太可能遇到一艘船，上面的人平均胡子长度是 3.4 毫米，或者 19.2 毫米。因为这些船上的人的胡子的平均值可以看作是样本的均值，我们用 $ \bar x $ 来注记。

欢迎关注微信公众号「Swift 花园」

样本和目标总体

几乎所有的统计研究都基于样本。

想象你试图知道伦敦有多少学生以嬉皮士自居，但你几乎不可能去问全部的学生这个问题。所以你决定采样，比方说 200 个调查对象，并估计有多少人把自己看做嬉皮士。

关于统计的一个好处是，它能基于仅仅这 200 个调查对象，即样本，帮助你得出关于伦敦所有学生的结论，即目标总体。这一节中，我将详细解释样本和目标总体。

如果你从目标总体约 300,000 个学生中选择 200 个调查对象作为样本，基本上你正在聚焦于总体的一个子集。如果你测量一组变量，比如性别，年龄，所在学校，等等。你可以做所有的计算，比如单一变量分析，包括众数、平均数和标准差，或者双变量分析，计算皮尔逊相关系数或者做回归分析。所有这些数字性总结都完全是基于样本，它们被称为 统计数字 (statistics) 。通常，这种总结样本数据的方法被称为 描述统计 (descriptive statistics) 。不过，在实际的研究实践中，我们经常对特定样本的总结不感兴趣 —— 我们的实际目标是对潜在的目标总体做出推断。

在我们的案例中，所有 300,000 个学生都在伦敦。如果我们借由样本中得到的数据推断关于总体的结论，那我们就是在使用 推断统计学 (inferential statistics) 的方法。 统计数字以罗马字母显示。例如，$ \bar x $ 代表平均数， s 是样本的标准差。 参数则以希腊字母显示， μ 代表总体的平均值， σ 代表总体的标准差。

想象你问这 200 个调查对象他们觉得自己有多大程度上把自己看做嬉皮士。他们可以从 0 到 10 表示自己嬉皮士的程度， 0 代表他 / 她根本不认为自己是嬉皮士，而 10 代表一个人完全将自己视为嬉皮士。

现在想象样本的 “嬉皮士值” 均值是 3.12 ，核心问题变成：目标总体的均值是多少？推断统计学可以帮助我们解答这类问题。