欢迎关注微信公众号「Swift 花园」

对于离散随机变量，有一个最重要的概率分布，它是 二项分布 (binomial distribution) 。二项分布处于二元数据。因为二元数据的情况非常多，所以二项分布使用频繁。

让我们从例子开始，你会在这些例子中看到两种结果。比如，参加会议是否迟到，投票赞成或者反对，噪音等级超过 80 分贝或者没有。当你收集这类现象的试验时，成功或者失败的数字服从二项分布。例如，你可以考虑每 25 个与会人员，有多少个迟到，或者投反对票的人有几个。

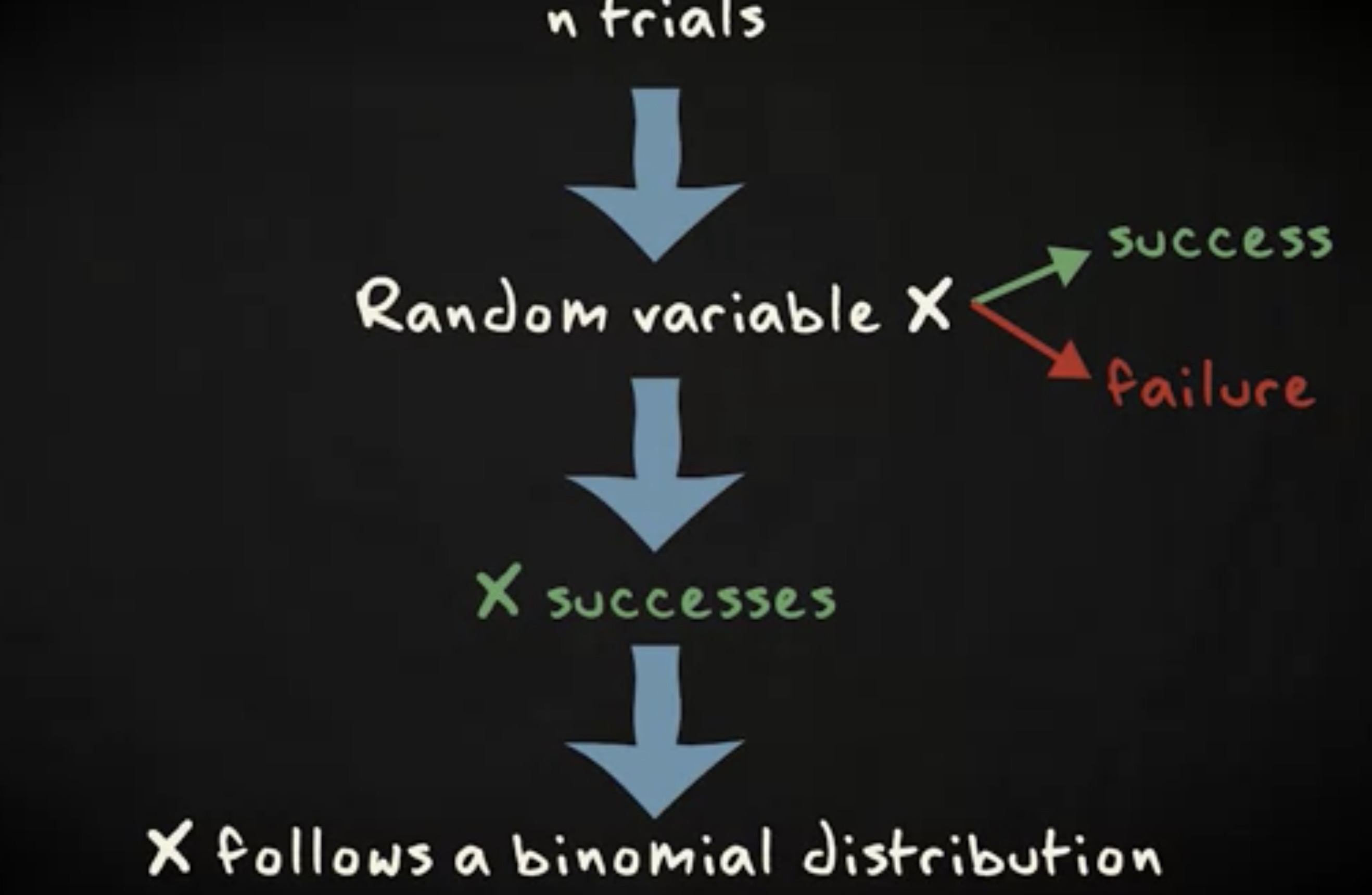
下面是你可以确定一个随机变量服从二项分布的条件：首先，每一个试验成功的概率相同；其次，试验在统计上是独立的 —— 即一个试验的结果不会影响其他试验。

实际上，你发现二项分布的三个要素。首先，试验现象有两种结果，并且成功概率是常量。这种实验被称为 伯努利试验验 (Bernoulli trial) 。其次，你观察试验结果 n 次。第三，你对成功的结果计数，记为 x 。这三个元素被结合成一个公式，它给出了在 n 次试验中取得特定数量成功结果的概率。公式如下：

$$P (x) = \frac {n!}{x!(n - x)!} p^x (1 - p)^{n-x}, x = 0,1,2,...,n$$

你可以直接把 n，x 和 p 填进公式从而获得答案。

如公式所示，随机变量 x 只能取 0 到 n 的值。这很合理，因为你只能有有限次成功，0 ，1 ， 2 ，直到 n 。因此这个公式是一个概率质量函数，它直接给出了匹配每个可能的 x 的概率值，你不必像考虑概率密度函数那样考虑区间。

感叹号不常见，它表示 阶乘法 (factorial) ，即把所有从 1 到指定的整数全部相乘的结果。例如， 4 阶乘等于 1 乘以 2 乘以 3 乘以 4 。 公式前部的这个阶乘的除法实际上是给出了无视顺序，从 n 个元素中选出 x 个元素的方法，它也被称为 二项系数 ( binomial coefficient) ，有的时候也速记为 $ C^x_n $ 。

现在，让我们把二项公式应用到特定的例子里吧。想象你每天通勤的路线上需要经过一座吊桥。这桥有 10% 的时间是打开的，但打开时机是随机的。那么你在一周中碰到 0 ， 1， 2 ，直到 5 天的概率是多少呢？

实验有 5 次试验，遇到打开的桥的概率是 0.1 。因此，这里的二项分布的概率如下：

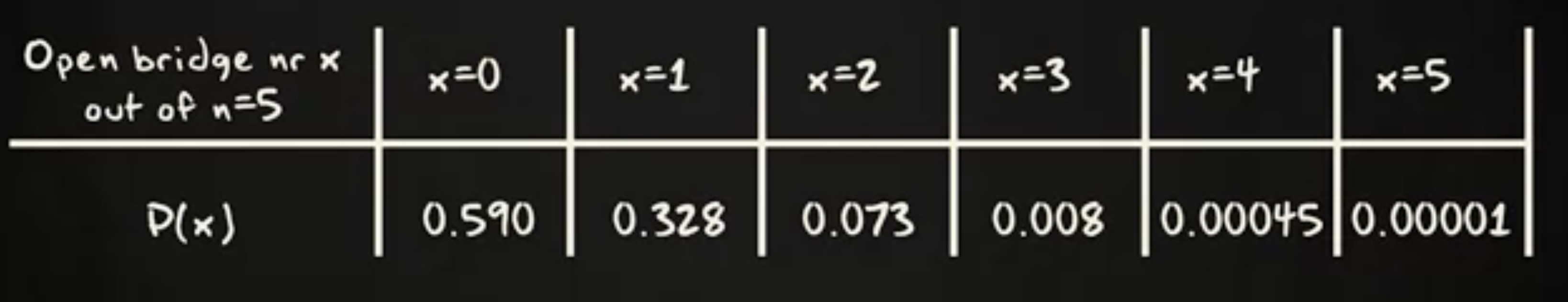
如果你把 6 个概率和 x 相乘并加总，你会发现这个值等于 1 。本应如此。

欢迎关注微信公众号「Swift 花园」

正态分布 (normal distribution) 的函数形式

在所有的概率分布中，有一个特别出众，我们经常遇到。它就是 正态分布 (normal distribution) 。

在本节中，我们会学习它的重要属性。正态分布又被称为 高斯分布 (gaussian distribution) 。它是对称的，钟形，以均值 μ 和 标准差 σ 为特征。分布的最高点是均值的位置，宽度则由标准差指定。均值 μ 和 标准差 σ 被称为正态分布的 参数 (parameters) 。

正态分布的累积概率分布是一个 S 函数曲线 (sigmoideal shape) ，均值处于概率为 0.5 的地方，标准差决定了曲线的陡峭程度。

随机变量 X 有一个均值 μ ，标准差 σ 的正态分布，可以速记为：

$$X \sim N (\mu, \sigma^2)$$

而下面这个等式描述了完整的概率密度：

$$f (x)=\frac {1}{\sqrt {2\pi}\sigma} e^{-0.5\left (\frac {x-\mu}{\sigma}\right)^2}$$

这个方程之所以重要，并非因为它第一眼看起来很复杂 —— 包含了三个重要的数学常量，$ \pi $，$ e $ 和 2 的平方根，还因为它连接了统计国王和物理世界。这个方程可以描述粒子扩散的过程。如果你释放一个扩散物，比如放一块糖到茶里，茶里的糖将按照这个方程的规律扩散。不仅流体是这样，大气中的颗粒物，道路交通，社会中的信息，都遵循这个分布的规律。

欢迎关注微信公众号「Swift 花园」

随机变量的平均数

在了解了随机变量的概率分布之后，我们可以开始对这种变量进行计算了。

首先，你需要知道，总结性统计 (summary statistics) ，跟观测数据相似，都能用来捕捉分布的本质。这一节中，我们要来研究概率分布的平均数，以及我们在调整随机变量或者组合随机变量之后，平均数如何变化。

以下将一个随机变量的平均数以 $ μ $ 注记，它表示对许多观测值预期的平均结果，因此也被称为随机变量的 期望值 (expected value) ，以 $ E $ 注记。

一个离散随机变量的平均数是所有可能的值乘以概率权重之后的均值，因此它等于每个可能的值乘以概率，然后加总。对于连续随机变量，同样的规则也适用。为了应对连续性，加总的计算被替换成积分 (integral) ，概率也不像离散那样被定义为 i ，而是 x 的函数。

举个例子，假设你正在一个熟悉的街区日常漫步，路上会经过三个交通灯。每等一个交通灯会使整个漫步多花 2 分钟。对于这三组交通灯的等待，你记录了等 0 个 到等 3 个的频率，下面是概率表：

你预期的等待时间计算方法如下，最后会得到 2 分 12 秒。有趣的是， 2 分 12 秒这个值实际永远不会发生。你要么不用等，要么就是等 2， 4， 6 分钟中的某个时间。

现在，让我们来审视一下随机变量的平均数。如果我们给随机变量 x 乘上一个系数再加上一个值， 变成 $ a + bx $ ，那么平均值会变成 $ μ_{a+bx} $ 。

欢迎关注微信公众号「Swift 花园」

随机变量和概率分布

随机变量的随机性其实并不像它的名字传递的那样多。这一节教程中，我将通过随机变量的可能结果和它们对应的概率来描述 概率分布 (probability distribution) 。换句话说，随机分布使随机性具体化，并且提供了一条在计算中使用随机变量的道路。当我们观察个体或者对象的时候，我们可以关注每个个体的若干个属性，这些属性就叫做 变量 。

现在，想象你收集了一份数据，并且决定重复实验。你能够找到相同的试验个体来测量变量，或者能找到相近的个体。不管采用哪一种，你会发现你的变量的值每次都不一样。这就是所谓的变量。举个例子，你测量一个人的身高几次，每次的结果可能会有几毫米到 1 厘米的偏离，这取决于你测量的时间在一天中的时刻，你的测量设备的精度，等等。

通常我们预料变量的值具有随机的变异性。如果这种概率的随机性是中肯的，则这个变量被称为 随机变量 (random variable) 。随机变量可以有一组可能的值，每个值都和概率关联。因此，如果随机变量的样本足够大，不同值的相对频率就接近概率。为了让表达更清晰，让我们用斜体的大写字母来表示随机变量，小写字母来表示它取到的值。

即 X 为随机变量，$ x_1, x_2, x_3, … $ 为随机变量的值。

随机变量有两种，一种是 离散的 (discrete) ，一种是 连续的 (continuous) 。离散随机变量可以有一组可数数量的不同值，比如 0 / 1 / 2 / 3 。实际上，如果一个随机变量只能取得有限数量的不同值，那它必定是离散的。离散随机变量的例子很多，比如一个家庭里小孩的数量。连续随机变量则可以取得无限数量的可能值。它通常是测量。为了演示无限性，假设一个身高值测出来是 3.1 米，如果换更精确的测量仪器，也许能测到 3.14 米。更精确的仪器，也许还能测到 3.145 米。换言之，通过更精确的测量，或者放大操作，无限数量的结果是可能的。年龄，温度，速度，这些都可以是连续随机变量的例子。

随机变量的值可以很方便地通过随机分布来呈现。随机分布的呈现形式可以是表格，图或者数学方程，并且是通过随机变量的每个取值关联的概率列表来定义的。

根据定义，每个随机变量都有一个概率分布，离散随机变量的概率分布叫 概率质量函数 ，而连续随机变量的概率分布叫概率密度函数。至于为什么有这种区别，稍后解释。

欢迎关注微信公众号「Swift 花园」

联合概率和边际概率

对有趣现象的计数，在日常生活中常常转换成比例，最终变为概率。利用概率估算的力量，可以更好地理解这些现象之间的关系或做出预测。 联合概率 (joint probability) 和 边际概率 (marginal probability) 是两个在这种情况下会用到的重要概率类型。在这一节教程中，我将解释联合概率和边际概率的含义，并展示它们的属性。

想象你在沙滩上观察你的海滩同伴。你会注意到三种不同类型的活动 —— 它们是互斥的。有的休息，他们都坐在或躺在沙滩上。有的玩，这些人到处乱跑，建造沙堡或站在水中。最后，有的在游泳。此外，你还可以按性别区分。所以你观察到的每个人都是一个案例.

在数据集中，性别和活动是变量。你最终得到以下结果的列联表。总共计了 113 人，其中有 79 人在休息，有 20 人在玩，并且他们中只有 14 人在游泳。女性和男性的数量，分别是 62 和 51 。

这些数字实际上是每行和每列变量位于此表边缘的总和，因此被称为边际值。请注意，这与口语上 “边缘的”，即并不重要的，并不是一回事。在表中边际值代表对于单个变量的说明，没有关于任何其他变量。例如说休息的人数不考虑性别。

现在，我们打开这个频率表通过将每个单元格数字除以总数 113 得到比例的表格。

在此表中，中心块包含六个位置，它们加起来等于一。同时，每列中的比例加总到底部的边缘行中的值，每行中的比例加总到右边的边缘列中的值。并且边缘行的值加起来等于边缘列的值加起来。